高等代数学习笔记（持续更新）

先说在最前面，博主不是数学专业的，是计算机类的，所以可能数学的语言的准确性和证明的严密性都不足。

一、行列式是什么？

由线性方程组推出行列式

用行列式去解线性方程组

二元线性方程组

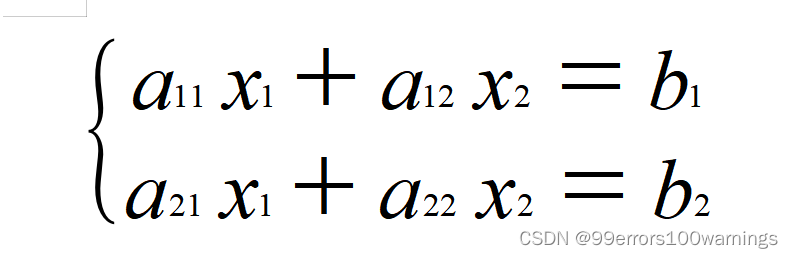
                                                                          式1

其中行列式就可以抽象为这两个方程组的系数

其中一个未知数的表达式如下：                                               

                                                                          式2

 用行列式表示：

 

式3

记住这个前提条件！！！！！！！！

式4

推广到多阶行列式的时候，公式4里面的未知量就变换为线性方程组等号左边的未知量即可。

本质上其他线性方程组的解都可以由于二元线性方程组推出，只需要替换分式上下的值就行了。

二、排列

由1,2,3，....，n组成的有序数组称为一个n阶排列。

n阶排序的总数是：n！

定义1：前面的数大于后面的数   就叫逆序数

定义2：一个排列中逆序的总数就叫做逆序数

定义3：逆序数为偶数的为偶排列，奇数的为奇排列

定理1：对换改变排列的奇偶性：奇变偶，偶变奇

定理2：任意一个n阶排列与排列12.....n都可以经过一系列对换互变，并且所作对换个数与这个排列有相同的奇偶性。