IEEE754浮点原理 - 计算机存储小数的误差有多少

老Z先生

已于 2024-06-06 07:18:28 修改

阅读量1k

点赞数 11

分类专栏：计算机基础文章标签：算法数据结构 mcu 物联网 iot c语言 c++

于 2024-05-21 07:00:38 首次发布

本文链接：https://blog.csdn.net/bitslink/article/details/139078980

版权

计算机基础专栏收录该内容

4 篇文章 0 订阅

订阅专栏

1. 背景

计算机内部直接能够存储的都是二进制整数，为了解决计算机能够解决处理存储小数问题，早期计算机使用定点小数方案，所谓定点小数即使用固定的位数来表示小数，如在8位数中可以使用5位来表示整数剩余3位来表示小数，使用定点小数方案存在两个问题，一个是为了不同的准确度每家处理处理都有自己的定点方案，在这种情况对软件开发的兼容性问题是灾难性的，另外一个问题是使用定点方案后所能表示的范围大大降低，如使用2位二进制位来表示小数，表示范围就会缩小4倍，这还是精度只有0.25的情况下，若需要更高表示精度，表示范围呈指数规律快速下降。

为了解决定点小数存在的问题，1980年intel在8087处理使用了浮点方案并被广泛应用后，于1985年被IEEE收录并成为IEEE 754 浮点标准。

2. 十进制小数到二进制小数的转换

对于一个十进制小数转换成二进制的小数，例如“10.625”表示成二进制小数最终形式是“XXX.YYY”,其中二进制整数“XXX”是对应十进制的整数部分，而二进制“YYY”是对应十进制的小数部分。

2.1. 整数部分转换

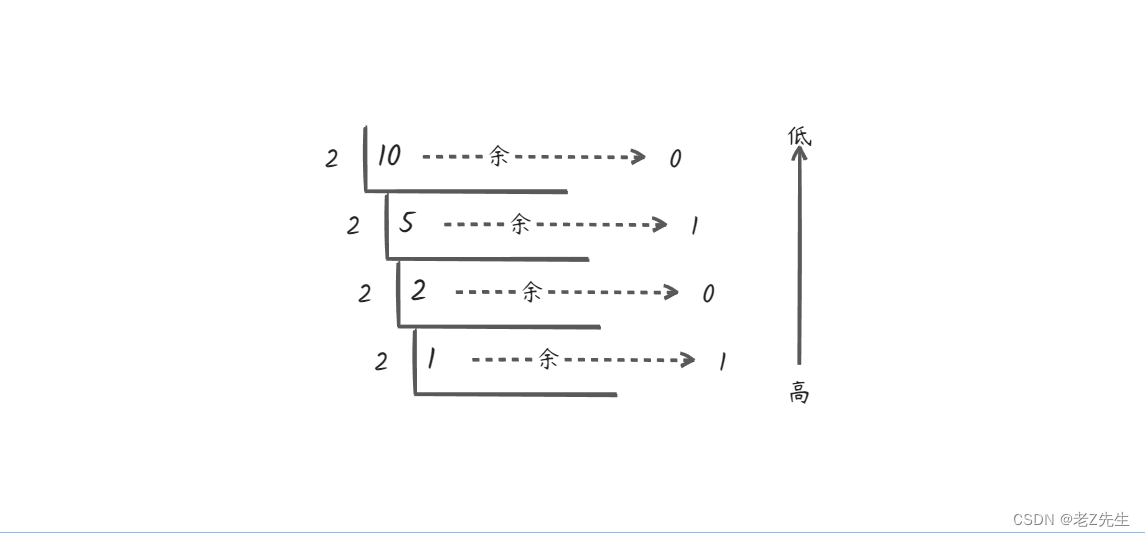
对于整数部分转换一般规律如下：

$Dec=B_0*2^0+B_1*2^1+···+B_n*2^n$

其中 $B_0$ 是二进制中的最低位， $B_n$ 是二进制中的最高位，由于是二进制他们要么为“0”要么为“1”，这里面存在一个规律---当最低位为“0”这个十进制一定是偶数，当最低二进制位为“1”这个十进制一定是奇数，反之也是成立的，即：十进制数为偶数二进制最低位为“0”，十进制为偶数二进制最低位为“0”，我仅需要知道这个数是奇数还是偶数就可以知道最低二进制位是“0”还是“1”，知道了二进制的最低位后带入上面式子就可以使用同样的方法算出二进制次低位。以上就是十进制整数转换成二进制方法（“除2取余,逆序排列”）的本质说明。
对于“10”转换二进制公式推导如下：

$10=B_0*2^0+B_1*2^1+B_2*2^2+B_3*2^3$

由于“10”为偶数，B0只能为"0"并将其结果带入上式：

$10=0+B_1*2^1+B_2*2^2+B_3*2^3\\ 10=B_1*2^1+B_2*2^2+B_3*2^3\\ 5=B_1*2^0+B_2*2^1+B_3*2^2$
上式B1成了二进制中的最低位，由于“5”为奇数，那么B1只能为“1”并带入上式：

$5=1*2^0+B_2*2^1+B_3*2^2\\ 4=B_2*2^1+B_3*2^2\\ 2=B_2*2^0+B_3*2^1\\$

上式B2成为了二进制中的最低位，由于“2”为偶数，那么B2只能是“0”并带入上式：

$2=0*2^0+B_3*2^1\\ 2=B_3*2^1\\ 1=B_3$
并最终十进制“10”对应的二进制数为“1010”,上面十进制数转换成二进制各个步骤流程较为严谨，但较为复杂，清楚了原理后就可以使用简便的“除2取余逆序排列”方法：

2.2. 小数部分转换

当清楚了整数部分的转换原理后，小数部分也类似，对于小数部分存在以下等式

$Frac=F_0*2^{-1}+F_1*2^{-2}+···+F_n*2^{-n}$

上式中Frac为十进制小数（格式如“0.xxx”），F0为二进制小数的最高位（最左边），Fn为二进制小数的最低位（最右边），这里已不能使用计算整数部分的方法了，在上式右边表达式要取得最大值，F0~Fn全为1，此时表达式为：

$\frac{1}{2}+\frac{1}{4}+···+\frac{1}{n}$

这其实是一个高等数学里面的一个等比无穷级数求和，求和结果并不是发散的，通过计算无穷项求和结果等于1，即无论多少项求和结果小于1。对等式乘以2，小数点向右边移动一位，F0变成整数位，F1~Fn级数求和小于1,那么F0就等于左边十进制的整数：

$2*Frac=F_0+F_1*2^{-1}+···+F_n*2^{-n+1}\\ F_0 = int(2*Frac)$

循环上述步骤，就可以把小数部分转换成二进制表示，另外还可以使用简便方法，例如对于小数部分“0.625”，采用“乘2取整，顺序排列”计算方法如下：

2.3. 转换工具

搞清楚转换原理后，就可以让计算机来执行这繁琐的转换步骤，由于在计算机中已采用浮点数据类型，一般都不会原生支持这个转换功能，以下这个网址可实现十进制小数到二进制小数的转换功能：

https://tool.oschina.net/hexconvert

3. IEEE754浮点小数

IEEE754浮点核心思想是采用了二进制的科学计数法（ $frac*2^e$ ），采用二进制科学计数法后就可以在精度和范围之间找到一个平衡点，在数值较小的时候精度或者分辨率极好，随着要表示的数值变大分辨率逐渐降低。

如上图所示IEEE 754用了了三部分来表示一个值，分别是sign符号位用来表示正负、exponent用于科学计数法的指数、fraction用于科学计数法的小数部分，计算表达式如下：

$float={(-1)}^{sign}*fraction*2^{exponent-bias}$

3.1. 单精度

在单精度中共存用存储空间4字节共32位，这三部分占用的空间如下：

内容	sign	exponent	fraction
占用空间	1bit	8bit	23bit
位置	bit31	bit30~bit23	bit22~bit0

在单精度中指数e取址被分成了三段，分别是0、1~254、255；另外bias取值127。

当exponent取址取值1~254时，这个浮点数被称为规约数，所谓规约数是指能用唯一确定的浮点形式去表示一个值，此时规约数很难与表示0和距离0较近的小数，此时表达公式如下：

$float={(-1)}^s*1.fraction*2^{exponent-127}$

当exponent取值0且fraction也取0时，此时表达式如下：

$float={(-1)}^s0$

当exponent取值0且fraction取非0时，这个浮点数被称为非规约数，一般仅在这个浮点数距离0较近才会使用，此时表达式如下：

$float={(-1)}^s*0.fraction*2^{-126}$

当exponent取值255且fraction也取0时，此时表达式如下：

$float={(-1)}^s*\infty$

当exponent取址取值255且fraction取非0时，此时表达非数（NaN）。

单精度的分段表达式如下：

$float = \begin{cases} {(-1)}^s*1.fraction*2^{exponent-127}, & \text{$2^{-126}$<=$flaot$<$2^{127}$,1<=$exponent$<254} \\ {(-1)}^s*0.fraction*2^{-126}, & \text{0<$flaot$<$2^{-126}$,exponent=0,fraction!=0} \\ {{(-1)}^s0}, & \text{$exponent$ = $0$,$fraction$ =0} \\ {{(-1)}^s*\infty},& \text{$exponent$ = $255$,$fraction$ = 0}\\ {NaN},& \text{$exponent$ = $255$,$fraction$ != 0}\\ \end{cases}$

3.2. 单精度浮点精度分析

在单精度浮点表达式存在分段且多输入，对： $(-1)^s*1.f*2^e$ 进行精度分析较为困难也不直观，这里实际的取值进行实际测试精度分析，对与任意一个值进行精度分析，我们将任意的一个值赋值给一个float型的变量，然后对其中的fraction最低字节加1会得到一个新的浮点数，用fraction加一会得到浮点和原来的浮点相减即可得到相邻两个浮点的差值，这个差值即为分辨率，C语言源码如下：

#include "stdio.h"
#include "stdint.h"

#define  NUM 11
int main()
{
    float ff[NUM];
    float yy[NUM];
    float dd[NUM];
    uint32_t *p;

    for(int i=0;i<NUM;i++)
    {
        if(0 == i)
        {
            ff[i] = 0.1;
            yy[i] = ff[0];
            p = (uint32_t *)&yy[i];
            *p += 1;
        }
        else
        {
            ff[i] = ff[i-1]*10;
            yy[i] = ff[i];
            p = (uint32_t *)&yy[i];
            *p += 1;
        }
        
        dd[i] = yy[i] - ff[i];

        printf("%0.2f\t %0.8f\n",ff[i],dd[i]);
    }

    printf("x=[");
    for(int i=0;i<NUM;i++)
    {
        printf("%0.2f,",ff[i]);
    }
    printf("]\n"); 
    printf("y=[");
    for(int i=0;i<NUM;i++)
    {
        printf("%0.9f,",dd[i]);
    }
    printf("]"); 
}

分辨率结果如下：

目标数	分辨率	分辨率（近似）
0.1	0.000000019	1.9*10-8
1.0	0.00000012	1.2*10-7
10.0	0.00000095	9.5*10-7
100.0	0.00000763	7.6*10-6
1000.00	0.00006104	6.1*10-5
10000.0（万）	0.00097656	9.8*10-4
100000.0（十万）	0.00781250	7.9*10-3
1000000.0（百万）	0.0625	6.2*10-2
10000000.0（千万）	1.0	1
1000000000.0（亿）	8.0	8
10000000000.0（十亿）	64.0	64

3.3. 双精度

在双精度中这三部分占用的空间如下：

内容	sign	exponent	fraction
占用空间	1bit	11bit	52bit
位置	bit63	bit62~bit52	bit51~bit0

双精度表达式与单精度类似。

3.4. 双精度浮点精度分析

双精度分辨率实测分析源码：

#include "stdio.h"
#include "stdint.h"

#define  NUM 11
int main()
{
    double ffd[NUM];
    double yyd[NUM];
    double ddd[NUM];
    uint64_t *pd;

    for(int i=0;i<NUM;i++)
    {
        if(0 == i)
        {
            ffd[i] = 0.1;
            yyd[i] = ffd[0];
            pd = (uint64_t *)&yyd[i];
            *pd += 1;
        }
        else
        {
            ffd[i] = ffd[i-1]*10;
            yyd[i] = ffd[i];
            pd = (uint64_t *)&yyd[i];
            *pd += 1;
        }

        ddd[i] = yyd[i] - ffd[i];

        printf("%0.2f\t %0.17lf\n",ffd[i],ddd[i]);
    }

    printf("x=[");
    for(int i=0;i<NUM;i++)
    {
        printf("%0.2lf,",ffd[i]);
    }
    printf("]\n"); 
    printf("y=[");
    for(int i=0;i<NUM;i++)
    {
        printf("%0.17lf,",ddd[i]);
    }
    printf("]"); 
}

分辨率结果如下：

目标数	分辨率	分辨率（近似）
0.1	0.00000000000000001	1*10-17
1.0	0.00000000000000022	2.2*10-16
10.0	0.00000000000000178	1.8*10-14
100.0	0.00000000000001421	1.2*10-14
1000.00	0.00000000000011369	1.1*10-13
10000.0（万）	0.00000000000181899	1.8*10-12
100000.0（十万）	0.00000000001455192	1.5*10-11
1000000.0（百万）	0.00000000011641532	1.2*10-10
10000000.0（千万）	0.00000000186264515	1.9*10-9
1000000000.0（亿）	0.00000001490116119	1.5*10-8
10000000000.0（十亿）	0.00000011920928955	1.2*10-7

4. 总结

本质上计算机内部使用浮点就是二进制小数的科学计算法表示，与相同长度的整数（如都为32位长度）相比能表示更大的范围，但是浮点并不是全范围内等精度，它会随着要表示的数的绝对值变大而精度逐渐变小。

老Z先生

关注

11
点赞
踩
21

收藏

觉得还不错? 一键收藏
0
评论
IEEE754浮点原理 - 计算机存储小数的误差有多少

本质上计算机内部使用浮点就是二进制小数的科学计算法表示，与相同长度的整数（如都为32位长度）相比能表示更大的范围，但是浮点并不是全范围内等精度，它会随着要表示的数的绝对值变大而精度逐渐变小。
复制链接

扫一扫