【模式识别】最小风险贝叶斯决策

贝叶斯公式

如果每一类在空间中互不相交，有清晰的决策边界，那么就没有必要用贝叶斯方法了。这种叫做确定统计分类。

如果这些类相互之间有重合，新的样本的特征落到一个重合区域，那么就要判断该样本属于某一类的概率。从而通过最小风险或最小错误率的公式来计算具体属于哪一类。这种叫做不确定统计分类。

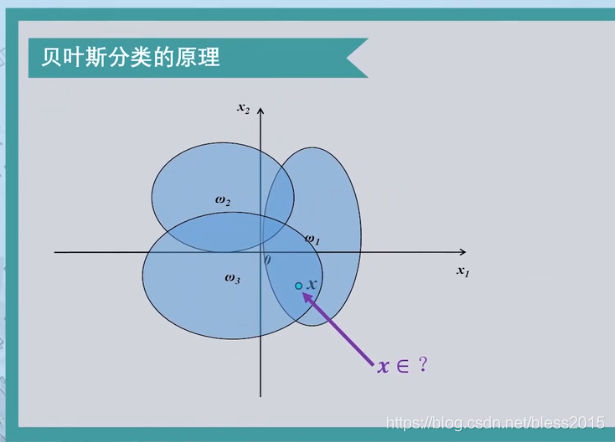
我们的训练数据是样本特征和样本标签。所以我们已知的是属于某一类的样本具有的特征。即知道某一类样本的统计分布特性。
这种分类方法就变成从这些数据中来推测具有某特征的样本属于哪一类。
把每一类样本整体出现的概率记做先验概率
$$P(w_i)$$
把某一类中的某样本特征出现的概率记做类条件概率
$$P(x|w_i)$$
把我们要计算某一个具体的样本特征值属于哪一类的概率记做后验概率
$$P(w_i|x)$$
用贝叶斯公式表示：
$$P(w_i|x)=\frac{P(x|w_i)P(w_i)}{P(x)}$$
首先来看右边，分布是全部样本空间的x，分子是属于某一个类的x的数量，所以两者的比值就是属于$w_i$类的$x$的数量占总$x$的数量的大小。（放到这里就是，数量就是可能性的概念，可能性有多少。是所有类别中，x的可能性之和）

贝叶斯分类特点：

1. 先验概率是计算后验概率的基础，是通过大量统计来得到的，这就是大数定理。而有人有说许多事件的发生不具有可重复性，所以先验概率只能根据对置信度的主管判断。
2. 那么就以新获得的信息对先验概率进行修正。
3. 分类决策一定存在错误率，即使错误率很低。

贝叶斯决策

不同的贝叶斯分类器有不同的贝叶斯决策

最小错误率分类器

这种最简单，就是把样本划分到后验概率大的那一类去。
$$P(w_i|x)=maxP(w_j|x)，j\in [1,c]$$
则$x\in w_i$
因为对于每一类，$P(x)$都相等，所以
$$P(x|w_i)P(w_i)=max[P(x|w_j)P(w_j)]$$
则$x\in w_i$
分析错误率

$$P(e)={\int }_{-\infty }^{+\infty }P(error,x)dx={\int }_{-\infty }^{+\infty }P(error|x)P(x)dx$$
$x$取不同值时，错误率的积分
$$P(error|x)=\sum _{j=1}^{c}P(w_j|x)-maxP(w_j|x)$$
最小错误率和最大后验概率两者等价。
对于最小错误率规则，确定了最小错误率也就确定了决策边界。也就是两个后验概率相等的点。

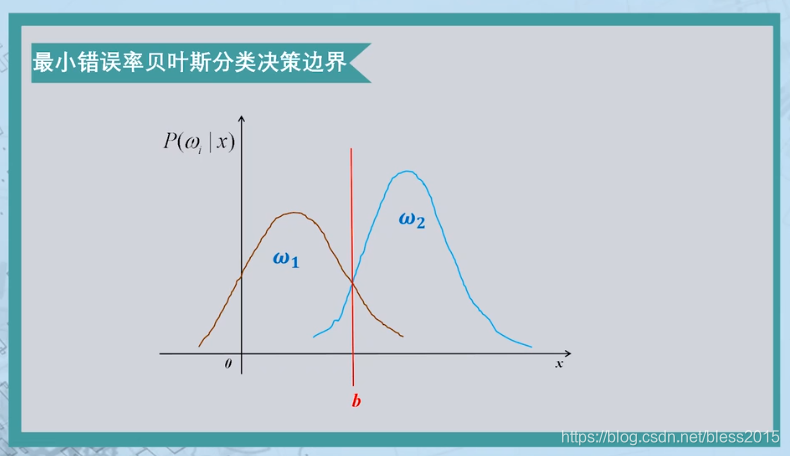
$$g(x)=P(w_1|x)-P(w_2|x)$$
$g(x)>0，x\in w_1$
$g(x)<0，x\in w_2$

但是最小错误率贝叶斯决策不一定是线性

最小风险错误率

该患者在出现症状后，实为H7N9的概率为（症状已经出现了）

同理：

则他出现症状是H7N9的概率为

但是如果出现误诊后，后果很严重，但是误诊为感冒则问题不大。所以仅仅考虑识别错误率不对，还要考虑后果。这就是最小风险错误率。
条件风险
$$R(a_i|x)=\sum _{j=1}^c{\lambda }_{ij}P(w_j|x)$$
对样本$x$，采取决策$a_j$的总风险

接上题，R是损失风险

最后取风险最小的决策，那就是诊断为H7N9。

朴素贝叶斯

在是用贝叶斯决策时，有两个条件必须是已知的：

1. 各种样本出现的整体先验概率
2. 各类中取得特征空间中某个点的类条件概率

先验概率可以从大量数据统计中得到，类条件概率需要从数据统计中估计，根据某一类的样本在各个维度上的特征值来估计其概率分布情况。这个概率分布，是一个各个特征维度上的联合概率分布，如果各个维度不独立，则估计很困难，如果各个特征相互独立，就叫朴素贝叶斯分类器。

正态分布下的贝叶斯决策

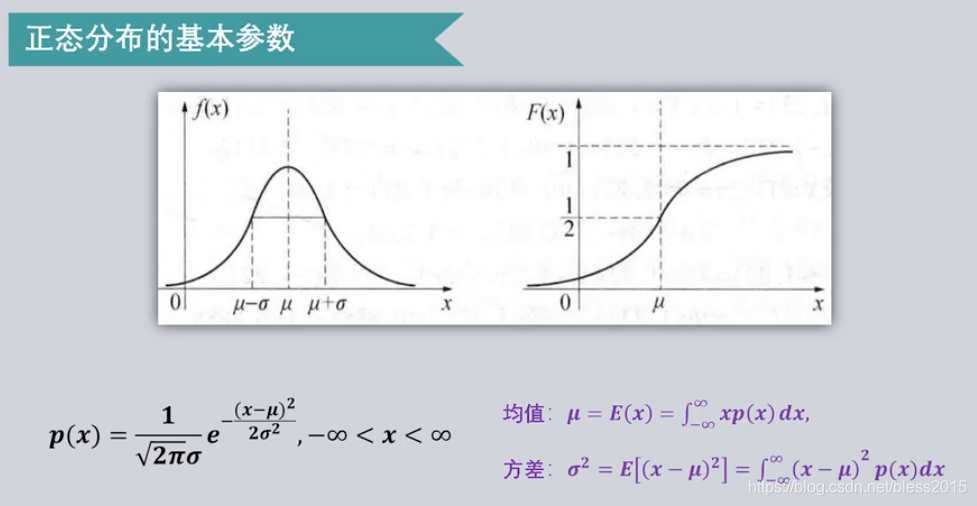
假设类条件概率符合二维正态分布，也就是$P(x|w_i)$

式子中有指数，不方便计算，取对数（指数函数是单调的）

中间的$-\frac{d}{2}ln2\pi$与计算无关

考虑不同情况：

每类协方差矩阵相等，先验概率相同

如果每一个样本的协方差矩阵都相等，类内各个特征维度间相互独立，且方差相同。
那么

则

因为先验概率都一样，所以可以 进一步简化

就是这种类型

这种情况被称为最小距离分类器，就是看x到各个类心的距离。

每类协方差矩阵相等，先验概率不同

每类的协方差矩阵都相等，各个特征维度都相互独立，方差相同，但是各类的先验概率不同，此时含有先验概率的项不能删除，就是只能将决策函数简化到

其中

由于$x^{T}x$与类别无关，可以删去，则决策函数简化为：

该判别式形式为线性判别形式

决策边界为

最后就是一个一大一小的圆

同一个维度下，各个分量的协方差为0，所以等概率的密度面是一个球面，这种情况下贝叶斯分类器具有线性决策边界。

每类协方差矩阵相等，先验概率相等，各个维度不相互独立

因为协方差矩阵和先验概率均与类别无关，则判别函数可以简化为

就是不能把协方差矩阵省略，所以就不能算$(x-u_i{)}^T(x-u_i)$了。
分类决策边界仍然是超平面，由于先验概率相等，则继续简化为

这时候这个距离不是欧式距离了，是马氏距离，所以这种情况叫马氏距离最小分类器

马氏距离考虑了特征之间的相关性，并且是尺度无关的。

协方差矩阵都相等，各个维度不相互独立，先验概率也不同

这时候的决策函数为

这种情况下，判别函数仍然是线性判别函数。分类决策边界仍然是超平面

此时的分类器是在马氏距离基础上，由先验概率修正的现行分类器，决策边界不与两个类别均值向量的连线垂直，也不会通过两个均值向量的中点，并且分类决策边界会偏向先验概率小的那一方。

协方差矩阵不相等，各个维度不相互独立，先验概率也不同

判别函数的二次项是与类别有关的，无法简化掉，所以这不是一个线性问题了。这时候是一个超二次曲面。

总结

只有各个类别样本同分布，贝叶斯分类器才是线性分类器。否则是一个二次项的非线性分类器。