HMM学习笔记2 隐马尔科夫模型与前向算法

一 序

   本系列文章摘自 52nlp（我爱自然语言处理: http://www.52nlp.cn/），原文链接在 HMM 学习最佳范例，有大佬做了二次整理，参见：https://blog.csdn.net/itplus/article/details/15335877

  本篇主要是整理隐马尔科夫模型的三个问题及前向算法。

二 三个问题

  2.1隐马尔科夫模型（Hidden Markov Models）

一个隐马尔科夫模型是一个三元组（π, A, B）。

  

在状态转移矩阵及混淆矩阵中的每一个概率都是时间无关的——也就是说，当系统演化时这些矩阵并不随时间改变。实际上，这是马尔科夫模型关于真实世界最不现实的一个假设。

2.2 应用

一旦一个系统可以作为HMM被描述，就可以用来解决三个基本问题。其中前两个是模式识别的问题：给定HMM求一个观察序列的概率（评估）；搜索最有可能生成一个观察序列的隐藏状态序列（解码）。第三个问题是给定观察序列生成一个HMM（学习）。

问题1计算概率（评估）

 　考虑这样的问题，我们有一些描述不同系统的隐马尔科夫模型（也就是一些( π,A,B)三元组的集合）及一个观察序列。我们想知道哪一个HMM最有可能产生了这个给定的观察序列。例如，对于海藻来说，我们也许会有一个“夏季”模型和一个“冬季”模型，因为不同季节之间的情况是不同的——我们也许想根据海藻湿度的观察序列来确定当前的季节。
　　我们使用前向算法（forward algorithm）来计算给定隐马尔科夫模型（HMM）后的一个观察序列的概率，并因此选择最合适的隐马尔科夫模型(HMM)。

总结：第一个问题是求，给定模型的情况下（给定的HMM模型参数已知），求某种观测序列出现的概率

问题2  预测问题（解码）

给定观察序列搜索最可能的隐藏状态序列。

另一个相关问题，也是最感兴趣的一个，就是搜索生成输出序列的隐藏状态序列。在许多情况下我们对于模型中的隐藏状态更感兴趣，因为它们代表了一些更有价值的东西，而这些东西通常不能直接观察到。
　　考虑海藻和天气这个例子，一个盲人隐士只能感觉到海藻的状态，但是他更想知道天气的情况，天气状态在这里就是隐藏状态。
　　我们使用Viterbi 算法（Viterbi algorithm）确定（搜索）已知观察序列及HMM下最可能的隐藏状态序列。

我们知道了观测序列,也知道了HMM的参数，让我们求出造成这个观测序列最有可能对应的状态序列。

问题 3  学习

   根据观察序列生成隐马尔科夫模型。
　　第三个问题，也是与HMM相关的问题中最难的，根据一个观察序列（来自于已知的集合），以及与其有关的一个隐藏状态集，估计一个最合适的隐马尔科夫模型（HMM），也就是求HMM的参数（π, A, B）。

  　当矩阵A和B不能够直接被（估计）测量时，前向-后向算法（forward-backward algorithm）被用来进行学习（参数估计），这也是实际应用中常见的情况。

由一个向量和两个矩阵(pi,A,B)描述的隐马尔科夫模型对于实际系统有着巨大的价值，虽然经常只是一种近似，但它们却是经得起分析的.

三 前向算法

3.1 穷举搜索（暴力法）

给定隐马尔科夫模型，也就是在模型参数（π, A, B)已知的情况下，我们想找到观察序列的概率。还是考虑天气这个例子，我们有一个用来描述天气及与它密切相关的海藻湿度状态的隐马尔科夫模型(HMM)，另外我们还有一个海藻的湿度状态观察序列。假设连续3天海藻湿度的观察结果是（干燥、湿润、湿透）——而这三天每一天都可能是晴天、多云或下雨，对于观察序列以及隐藏的状态，可以将其视为网格：  

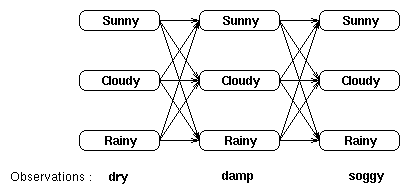
网格中的每一列都显示了可能的的天气状态，并且每一列中的每个状态都与相邻列中的每一个状态相连。而其状态间的转移都由状态转移矩阵提供一个概率。在每一列下面都是某个时间点上的观察状态，给定任一个隐藏状态所得到的观察状态的概率由混淆矩阵提供。

可以看出，一种计算观察序列概率的方法是找到每一个可能的隐藏状态，并且将这些隐藏状态下的观察序列概率相加。对于上面那个（天气）例子，将有3^3 = 27种不同的天气序列可能性，因此，观察序列的概率是：

Pr(dry,damp,soggy | HMM) = Pr(dry,damp,soggy | sunny,sunny,sunny) + Pr(dry,damp,soggy | sunny,sunny ,cloudy) + Pr(dry,damp,soggy | sunny,sunny ,rainy) + . . . . Pr(dry,damp,soggy | rainy,rainy ,rainy)

   看着简单，其实这个算法在现实中是不可行的。上面的例子为了讲解容易，状态值和观察值都很小，但是实际中的问题，隐状态的个数是非常大的。按照状态值是N个，观察值是K个。总共观察长度为T，我们的路径总个数就是N^T,（时间复杂度是是𝑂(𝑇𝑁^𝑇),指数级别的）光这个数据量就难以承受，到达了每个隐含状态的时候，还需要算一遍观察值出现的概率。

所以我们需要寻找在较低的时间复杂度情况下求解这个问题的算法。

3.2  前向算法

  前向算法，是基于动态规划思想求解。也就是说我们要通过找到局部状态递推的公式，这样一步步的从子问题的最优解拓展到整个问题的最优解。

  关于动态规划，可以看这篇入门 《算法图解》-9动态规划 背包问题，行程最优化

通常介绍前向算法会解释前向概率定义及推导过程

定义时刻𝑡t时隐藏状态为𝑞𝑖qi, 观测状态的序列为𝑜1,𝑜2,...𝑜𝑡o1,o2,...ot的概率为前向概率。记为：

 

𝛼𝑡(𝑖)=𝑃(𝑜1,𝑜2,...𝑜𝑡,𝑖𝑡=𝑞𝑖|𝜆)

推导过程我不贴了，我对公式真实看的头大。换个角度来理解。

我们首先定义局部概率（partial probability）,它是到达网格中的某个中间状态时的概率。然后，我们将介绍如何在t=1和t=n(>1)时计算这些局部概率。

　假设一个T-长观察序列是：

还是以天气为例，我们可以将计算到达网格中某个中间状态的概率作为所有到达这个状态的可能路径的概率求和问题。

例如，t=2时位于“多云”状态的局部概率通过如下路径计算得出：

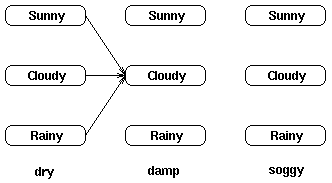
我们定义t时刻位于状态j的局部概率为at(j)——这个局部概率计算如下

对于最后的观察状态，其局部概率包括了通过所有可能的路径到达这些状态的概率——例如，对于上述网格，最终的局部概率通过如下路径计算得出：

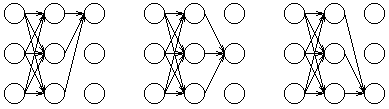
由此可见，对于这些最终局部概率求和等价于对于网格中所有可能的路径概率求和，也就求出了给定隐马尔科夫模型(HMM)后的观察序列概率。

下面是推导过程,熟悉的可以跳过。

计算t=1时的局部概率

特别当t=1时，没有任何指向当前状态的路径，所以t=1时位于当前状态的概率是初始概率，t=1时的局部概率等于当前状态的初始概率乘以相关的观察概率：

2.计算t>1时的局部概率

再看上面的公式，根据递归的思路，乘号左边项“Pr( 观察状态 | 隐藏状态j )”已经有了，现在考虑其右边项“Pr(t时刻所有指向j状态的路径）”。

为了计算到达某个状态的所有路径的概率，我们可以计算到达此状态的每条路径的概率并对它们求和，例如：

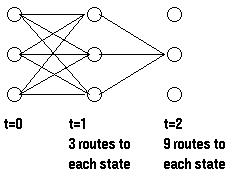
计算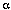所需要的路径数目随着观察序列的增加而指数级递增，但是t-1时刻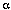给出了所有到达此状态的前一路径概率，因此，我们可以通过t-1时刻的局部概率定义t时刻的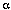，即：

其中N表示隐藏状态的数目。

　故我们所计算的这个概率等于相应的观察概率（亦即，t+1时在状态j所观察到的符号的概率）与该时刻到达此状态的概率总和——这来自于上一步每一个局部概率的计算结果与相应的状态转移概率乘积后再相加——的乘积。

现在我们就可以递归地计算给定隐马尔科夫模型(HMM)后一个观察序列的概率了——即通过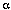(1)计算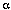(2)，通过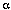(2)计算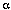(3)等等直到t=T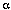(T)。给定隐马尔科夫模型(HMM)的观察序列的概率就等于t=T时刻的局部概率之和

时间复杂度对比

由于每次递推都是在前一次的基础上进行的，所以降低了复杂度（计算只存在于相邻的俩个时间点）。每个时间点都有N种状态，所以相邻两个时间之间的递推消耗N^2次计算。

而每次递推都是在前一次的基础上做的，所以只需累加O(T)次，所以总体复杂度是O(T)个N^2，即0（TN^2）,这比起暴力法的复杂度已经好了太多了(没找到图，大家可以看下指数型增长的曲线)。

注：穷举搜索的时间复杂度是2TN^T，前向算法的时间复杂度是N^2T，其中T指的是观察序列长度，N指的是隐藏状态数目。

总结

　我们的目标是计算给定隐马尔科夫模型HMM下的观察序列的概率。它在计算中利用递归避免对网格所有路径进行穷举计算。

  给定这种算法，可以直接用来确定对于已知的一个观察序列，在一些隐马尔科夫模型（HMMs）中哪一个HMM最好的描述了它——先用前向算法评估每一个（HMM），再选取其中概率最高的一个。

如果你觉得自己明白了，那么可以做个题验证下：

这是一个盒子与球的模型，例子来源于李航的《统计学习方法》。

　　　　假设我们有3个盒子，每个盒子里都有红色和白色两种球，这三个盒子里球的数量分别是：

盒子	1	2	3
红球数	5	4	7
白球数	5	6	3

　　　　按照下面的方法从盒子里抽球，开始的时候，从第一个盒子抽球的概率是0.2，从第二个盒子抽球的概率是0.4，从第三个盒子抽球的概率是0.4。以这个概率抽一次球后，将球放回。然后从当前盒子转移到下一个盒子进行抽球。规则是：如果当前抽球的盒子是第一个盒子，则以0.5的概率仍然留在第一个盒子继续抽球，以0.2的概率去第二个盒子抽球，以0.3的概率去第三个盒子抽球。如果当前抽球的盒子是第二个盒子，则以0.5的概率仍然留在第二个盒子继续抽球，以0.3的概率去第一个盒子抽球，以0.2的概率去第三个盒子抽球。如果当前抽球的盒子是第三个盒子，则以0.5的概率仍然留在第三个盒子继续抽球，以0.2的概率去第一个盒子抽球，以0.3的概率去第二个盒子抽球。如此下去，直到重复三次，得到一个球的颜色的观测序列:

𝑂={红，白，红} ，       求：得到观测序列“红白红”的概率是多少？

　　　　 注意在这个过程中，观察者只能看到球的颜色序列，却不能看到球是从哪个盒子里取出的。

　　　　那么按照我们上面HMM模型的定义，我们的观察集合是:

                 V={红，白}，M=2

　　　　我们的状态集合是：

               Q={盒子1，盒子2，盒子3}，N=3

　　　　而观察序列和状态序列的长度为3.

　　　　初始状态分布为：π 、状态转移概率分布矩阵为：A，　观测状态概率矩阵为：B