高中数学-三角函数之常见题型总结

相关公式

新教材，取消了和差化积与积化和差的三角函数题目

---

例题1

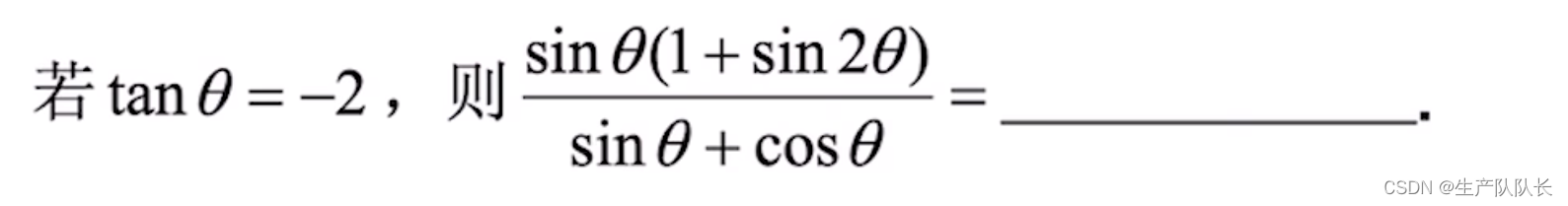
解析
根据条件tanθ = -2，我们应该就要想到，把待求式的角向θ靠拢
所以要想到如何降角，将2θ化成θ，那么，想到的公式就是：正弦函数的2倍角公式
另外
1 ± sin2θ = (sinθ)^2 + (cosθ)^2 ± 2sinθcosθ = (sinθ ± cosθ)^2

---

例题2

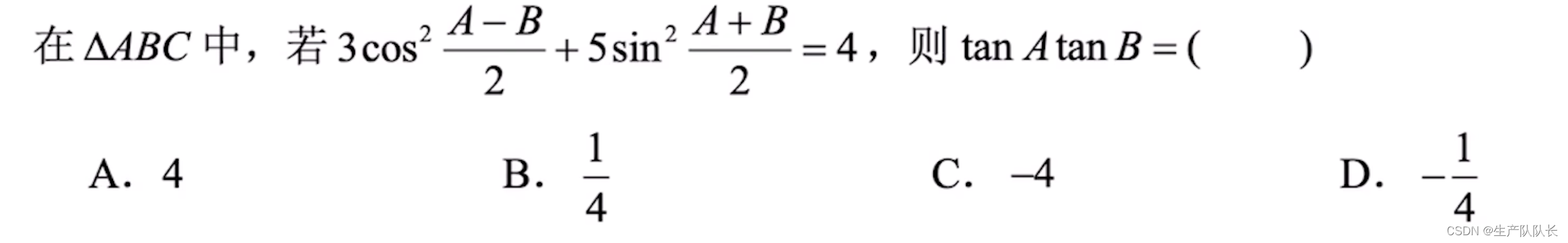
解析
我们看到(A-B)/2、(A+B)/2，但是，待求式的角是A、B。
此时，我们应该想到，如何升角，那么，想到的公式就是：正弦余弦的升角降幂公式

---

例题3

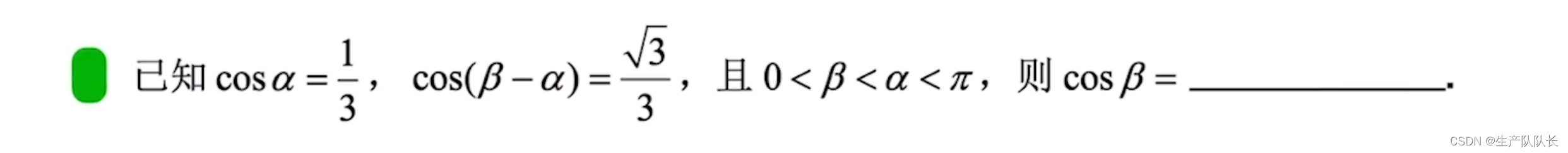
解析
这道题，有三个角，α、β、β-α。
首先，我们要确定三个角的范围
其次，我们要用条件中的两个角α、β-α，去表示出待求是中的角β
显然，α+β-α=β
最后，cosβ=cos(α+β-α)，则可以用余弦函数的两角和差公式展开，秒杀。

---

例题4

解析
这里只有一个θ角的变量，其他，都是常数
然后，对θ进行加减乘除运算得到的新角
这种情况，我们首先想到，整体换元法，来找到两个角的关系，最终，转化为同角三角函数问题
1、求新角的范围
2、利用公式找关系
这里主要用到了正切函数的二倍角公式和正切函数的两角和差公式

---

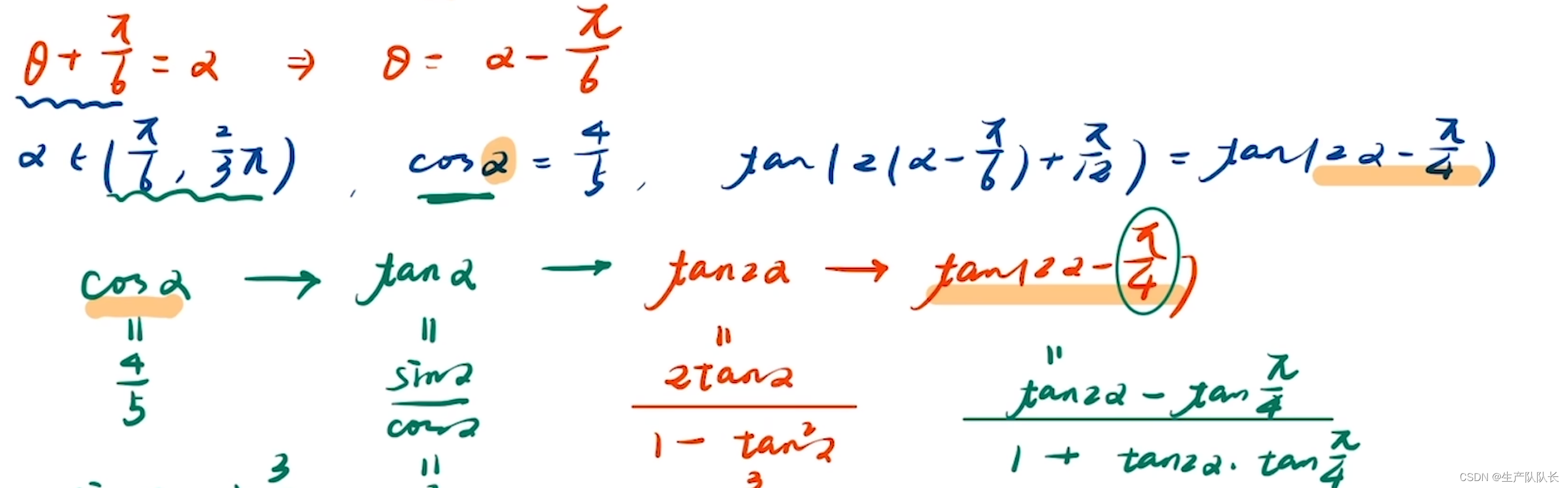
例题5

解析
解法1
把sin2θ向tanθ转化

解法2
将tanθ向sin2θ转化

显然，第二种方法更简便高效。
所以，遇到tanx，去求sinx，cosx型的题目，建议，把tanx化成sinx/cosx后，计算

---

例题6

解析
这一题，将三角函数和均值不等式结合进行考查
从待求式，我们应该要想到，此题用两角和差公式
再由其形式，我们又应该想到，用cos(α±β)
又由于条件给的是α-β，所以，我们最终应该选择cos(α-β)
这样，就转化成均值不等式的问题了