神机百炼2.49-朴素SPFA-CSDN博客

本文链接：https://blog.csdn.net/buptsd/article/details/124912383

朴素SPFA

本篇感想：

食用指南：

对该算法程序编写以及踩坑点很熟悉的同学可以直接跳转到代码模板查看完整代码
只有基础算法的题目会有关于该算法的原理，实现步骤，代码注意点，代码模板，代码误区的讲解
非基础算法的题目侧重题目分析，代码实现，以及必要的代码理解误区

题目描述：

给定一个 n 个点 m 条边的有向图，图中可能存在重边和自环，边权可能为负数。
请你求出 1 号点到 n 号点的最短距离，如果无法从 1 号点走到 n 号点，则输出 impossible。
数据保证不存在负权回路。

输入格式
第一行包含整数 n 和 m。
接下来 m 行每行包含三个整数 x,y,z，表示存在一条从点 x 到点 y 的有向边，边长为 z。

输出格式
输出一个整数，表示 1 号点到 n 号点的最短距离。
如果路径不存在，则输出 impossible。

数据范围
1≤n,m≤10⁵,
图中涉及边长绝对值均不超过 10000。

输入样例：
3 3
1 2 5
2 3 -3
1 3 4
输出样例：
2
题目来源：https://www.acwing.com/problem/content/853/

题目分析：

图：有向稀疏图，不存在负权回路
单源最短路 -> Dijkstra / 堆优化Dijkstra / bellman-ford
边权可能为负 -> bellman-ford
时间复杂度：bellman为O(nm) 达10¹⁰,严重超时
下面我们来讲改良了bellman-ford的SPFA
对bellman-ford不熟悉的同学先去看bellman-ford

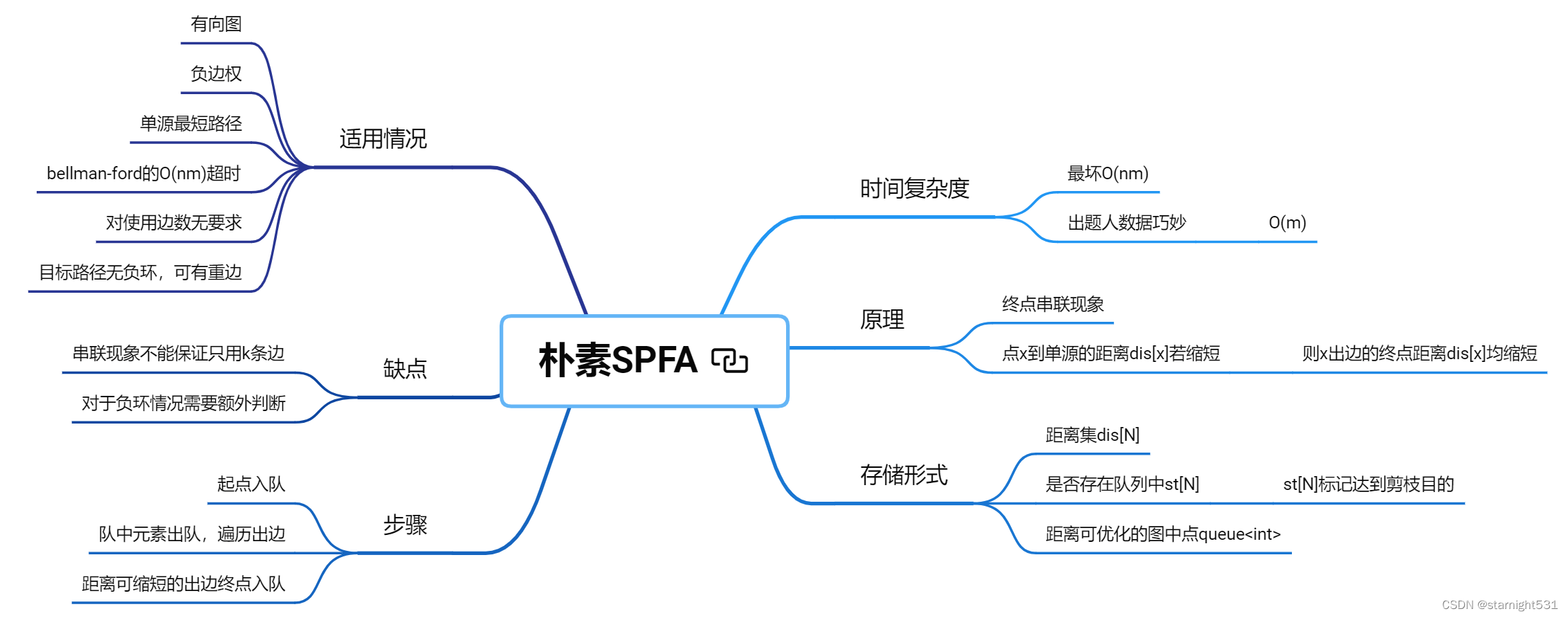
算法原理：

模板算法：

传送门：朴素Dijkstra
传送门：堆优化Dijkstra
传送门：bellman-ford

SPFA：

1. bellman-ford值得优化的点：

回顾bellman-ford的四步：
1. 静态数组/结构体读边
2. n-1次大循环
3. backup[]存储更新前节点距离
4. 遍历边，尝试用边将终点距离dis[]缩短
距离拷贝backup[]就是为了防止出现终点串联的现象
优点是达到最多使用k条边的目的
缺点是降低了速度
SPFA就是利用终点串联提升寻找最短路径的速度

2. SPFA优化方式：

一点到单源的距离若想减少，则需一条边，
满足边长 + 起点到单源距离 < 终点到单源距离
SPFA中，使用队列维护所有距离可能减少的点
1. 入队：
  一旦一点到单源的距离缩短，则入队
2. 出队：
  一点作为起点出队，遍历其所有边，将所有利用起点可缩短距离的终点入队

3. 存储形式：

图的存储：
由于需要分清每个点引出多少条边，所以不能单纯以结构体存储边了
图以邻接表形式进行存储，一方面是题目暗示，另一方面是遍历邻接表便于查找边的终点

邻接表5件套：idx h[起点] val[终点] ne[节点] memset(h, -1, sizeof h)
外加边长：w[]
可优化点的存储：

队列：STL中的queue
不手动静态队列，也就不再需要hh tt了
到单源距离集：

int dis[N];
队列中点标记：

int st[N];

若一点已经存在于优化队列中，则不重复将其加入优化队列，理由在代码误区板块

4. SPFA缺点：

由于利用了串联效应，所以不知道到某点到底经过了多少边，不能解决限定使用边数的问题
若负权环存在在目标路径中，则朴素SPFA队列始终不空，程序运行不停。
负环SPFA可以判断路径中存在负环，而停止运行，这个下一篇讲

5. 时间复杂度：

图中所有连通节点都入队列一次，O(n)
出队遍历出边终点，共计m条边，总计O(m)
时间复杂度：最坏O(nm)，和bellman同

但是出题人一般给SPFA的题目数据设计的很好，时间复杂度都是O(m)

代码实现：

#include <iostream>
#include <algorithm>
#include <queue>
#include <cstring>
using namespace std;
const int N = 100010;
int n, m;
int h[N], val[N], ne[N], w[N], idx;
void insert(int x, int y, int z){
    val[idx] = y;
    w[idx] = z;
    ne[idx] = h[x];
    h[x] = idx++;
}

int dis[N];
bool st[N];
void SPFA(int start){
    memset(dis, 0x3f, sizeof(dis));
    queue<int> que;
    
    dis[start] = 0;
    st[start] = 1;
    que.push(start);
    
    while(que.size()){
		int t = que.front();
        que.pop();
        st[t] = 0;
        for(int i=h[t]; i!=-1; i=ne[i]){
			if(dis[val[i]] > dis[t]+w[i]){
				dis[val[i]] = dis[t]+w[i];
                if(!st[val[i]])
               	que.push(val[i]);
                st[val[i]] = 1;
            }
        }    
    }
}
int main(){
    cin >>n >>m;
    memset(h, -1, sizeof(h));
    while(m--){
        int x, y, z;
        cin >>x >>y >>z;
        insert(x, y, z);
    }
    int start = 1;
    SPFA(start);
    if(dis[n] > 0x3f3f3f3f / 2) cout<<"impossible";
    else cout<<dis[n];
}

代码误区：

1. 入队/出队含义？

凡是dis[]目前还可以缩短的都入队
凡是dis[]目前已经停止缩短的都准备出队，为出边终点做贡献

2. 为什么为节点添加队列中标记st[N]?

其实不添加st[]标记数组也可以，
每次dis[x]一缩短就进入队列中也可以，
但是耗时增加了
下面这种情况：
1号入队列，1号出队列时将dis[2]dis[5]缩短
2 5入队列

2出队列将dis[3] dis[4]缩短，3 4入队列

5出队列将dis[4]缩短，此时发现4已经在队列中了，且在目前所有可优化dis[4]的节点后面

至于dis[4]已经被优化完成，4入节点的目的就是去优化4出边终点dis[]了

所以即使队列中只有一个4号节点，也不影响dis[4]和dis[4出边终点]
4号节点作为起点去优化出边终点的dis[]时候出队，st[4]=0，表示4的距离和4出边终点的距离都结束了

只有当dis[4]被后来队列中的点给优化后，dis[4]再入队