最大连续子序列和

问题描述

给定一个整数序列，$a_0,a_1,a_2,...,a_n$（可正可负），求其中最大的子序列和。如果所有整数都是负数，那么最大子序列和为0；

用数学语言描述， 就是：
求 $max(0,\sum _i^j{a}_i),0\le i\le j\le n$

穷举法

根据上述式子， 我们可以枚举上下界$i$和$j$， 然后在给定$i$和$j$时， 求出此区间的和。
这样可以枚举所有的和， 再找出最大值。
这种算法时间复杂度为$O(n^3)$.

int maxSubSequence1(int arr[], int size) {
    if (size <= 0) {
        return 0;
    }

    int i, j, k;
    int currSum = 0, maxSum = 0;

    for (i = 0; i < size; i++) { // 起点
        for (j = i; j < size; j++) { // 终点
            currSum = 0;
            for (k = i; k <= j; k++) { // 求出给定区间i, j的和
                currSum += arr[k];
            }

            if (currSum > maxSum) {
                maxSum = currSum;
            }
        }
    }

    return maxSum;
}

优化的穷举法

上述代码最内层的for有点多余， 因为它在每次改变“终点”$j$时， 都把currSum重置为0了， 其实我们可以利用之前的结果， 比如：
已知第1个到第5个的和为sum1, 那么第1个到第6个的和就可以用sum1再加上第6个元素。
这样的话， 就剩下两层for循环了， 时间复杂度为$O(n^2)$.
也就是：

int maxSubSequence2(int arr[], int size) {
    if (size <= 0) {
        return 0;
    }

    int i, j, k;
    int currSum = 0, maxSum = 0;

    for (i = 0; i < size; i++) { // 起点
        currSum = 0; // 起点更新时， 重置currSum
        for (j = i; j < size; j++) { // 终点
            currSum += arr[j]; // 终点改变， 在前一次的基础上加

            if (currSum > maxSum) {
                maxSum = currSum;
            }
        }
    }
    return maxSum;
}

看到$O(n^2)$的算法， 我们不免要想，能不能变成$O(n\log n)$呢？ 答案是可以的。
这里可以采用分治的思想， 对一个给定的整数序列， 将其从中间一分为二，

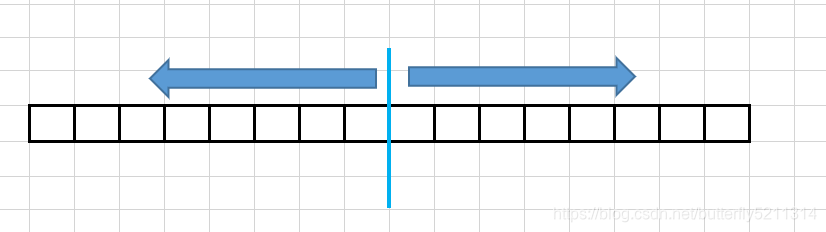
此时最大连续子序列和的存在有有3种情况：

• 在左半序列
• 在右半序列
• 所求序列刚好横跨中点，即左右序列各占一部分。

前两种情况和原问题一样， 不过规模变小了， 可递归解决。
对最后一种， 可以求出以中点为起点向左的最大连续序列和、以中点为起点向右的最大连续序列和，这两个结果的和就是第三种情况的答案。
此时算法的复杂度为$O(n\log n)$.

static int divide(int arr[], int left, int right) {
    if (left == right) { // 只有一个元素时
        return arr[left] > 0 ? arr[left] : 0;
    }

    int mid = (left + right) >> 1;
    int lMaxSum = divide(arr, 0, mid); // 左边部分最大和
    int rMaxSum = divide(arr, mid + 1, right); // 右边部分最大和

    // 中间部分求解
    int currSum = 0, lTmpMax = arr[mid], rTmpMax = arr[mid + 1];
    int i;
    for (i = mid; i >= left; i--) {
        currSum += arr[i];
        if (currSum > lTmpMax) {
            lTmpMax = currSum;
        }
    }

    currSum = 0;
    for (i = mid + 1; i <= right; i++) {
        currSum += arr[i];
        if (currSum > rTmpMax) {
            rTmpMax = currSum;
        }
    }

    // 第三种情况的答案
    int maxSum = lTmpMax + rTmpMax;

    // 三个和 求最大
    if (lMaxSum > maxSum) {
        maxSum = lMaxSum;
    }
    if (rMaxSum > maxSum) {
        maxSum = rMaxSum;
    }

    return maxSum;
}

int maxSubSequence3(int arr[], int size) {
    if (size <= 0) {
        return 0;
    }
    return divide(arr, 0, size - 1);
}

上述的maxSubSequence3， 为了让它和前两种参数形式保持一致， 引入了中间函数divide.

“扫描法”

姑且叫它扫描法吧。
首先说这样一个事实，

• 要求的子序列必然是以正数开头的，因为如果以负数开头，那么去掉开头的负数，会得到一个更优解。
• 如果我们已经对中间一部分序列 求得和为sum<0, 那么这部分不会是最终结果的一部分， 因为去掉它之后， 会得到一个更优解。

int maxSubSequence4(int arr[], int size) {
    if (size <= 0) {
        return 0;
    }
    int i = 0, currSum = 0, maxSum = 0;
    for (; i < size; i++) {
        currSum += arr[i];

        // 如果当前和大于maxSum, 则更新maxSum
        if (currSum > maxSum) {
            maxSum = currSum;
        }

        // 如果currSum<0， 则重置currSum， 即抛弃currSum对应的那些元素
        else if (currSum < 0) {
            currSum = 0;
        }
    }

    return maxSum;
}

测试程序如下：

int main(int argc, char const *argv[])
{
    int arr[] = {1, 2, 3, 4, -4, 5, -5, 6, -20};
    int size = sizeof(arr) / sizeof(int);

    printf("%d\n", maxSubSequence1(arr, size));
    printf("%d\n", maxSubSequence2(arr, size));
    printf("%d\n", maxSubSequence3(arr, size));
    printf("%d\n", maxSubSequence4(arr, size));
    return 0;
}

参考：
http://www.cnblogs.com/conw/p/5896155.html

欢迎补充指正！