3.Reducing Loss（减少误差）

1.machine learning model iteratively（迭代） reduces loss

通过输入特征值，通过模型预测，然后与标签比较，计算出误差，更新相关参数，重新进行预测，直至找到最佳参数（即误差最小）。上图即展示了机器学习算法如何训练模型。

迭代策略在机器学习中十分普遍，对于大量数据集的测量表现良好。

对于以下线性回归模型，输入一个或多个特征值，输出一个预测值y',为了简化，我们只考虑输入一个特征值，返回一个标签的情况。

$$y^{\prime }=b+w_1{x}_1$$

对于线性回归问题，b， w1 的初始值并不重要，可以随机选取。

• $b$ = 0
• $w_1$ = 0

代入得y'=0。

计算误差过程（computing loss）中，我们采用平方差公式，将下面两个参数代入

• y': The model's prediction for features x
• y: The correct label corresponding to features x.                                                                                                      
• 最后进入computing parameter update中，该部分机器学习算法会产生一个新的 b、${\mathrm{w1值\; 。然后不断迭代直至找到最低的误差所对应的参数值\; ，于是我们称最后的模型为收敛的（converge）。}}^{}$

${\mathrm{Key\; Point:}}^{}$

A Machine Learning model is trained by starting with an initial guess for the weights and bias and iteratively adjusting those guesses until learning the weights and bias with the lowest possible loss.

Key Terms

convergence 收敛 聚集	loss 误差
training训练 2.Gradient Descent（梯度下降）

对于这种回归问题，wi与误差的曲线是凹形的（convex）,如下图所示

                            

凸面问题只有一个最小值，就是曲线只有一个地方斜率为0,那就是误差最小的位置。梯度下降（gradient descent）是在机器学习中十分受欢迎的技巧。

第一步是找一个初始值给w1，这个初始值是无关紧要的，所以大多数算法是设置为0或者任意随机数。下图表示一个稍微比0大的初始点。

计算误差的算法会计算出当前位置的误差。梯度是一个偏导后的矢量，就等于曲线上的该点的导数。

既然梯度是一个矢量，所以它应该有两个特点：

• a direction 方向
• a magnitude 数量

梯度的方向总是沿着误差下降最快的方向，为了确定下一个检测的点，将梯度的大小加到起始点，如下图

算法会不断重复这个过程，直至找到斜率为0的点。

Key Terms

gradient descent梯度下降

step 步

3.Learning Rate（学习速率）

  Gradient descent algorithms multiply the gradient by a scalar known as the  learning rate（学习速率）  

(also sometimes called  step size ) to determine the next point. For example, if the gradient magnitude is

2.5 and the learning rate is 0.01, then the gradient descent algorithm will pick the next point 0.025

away from the previous point.

梯度下降度量下一个点时的单位被叫做学习速率，也叫作步长，如果梯度大小为2.5，学习速率为0.01，那么下一个点距离原先点的距离为0.025.

Hyperparameters（超参数） are the knobs that programmers tweak in machine learning algorithms. 超参数是机器学习算法的门把手，程序会花相当一段时间来调整学习速率，如果学习速率过小，则学习时间会很长，过大则会略过最优点。如下两张图所示：

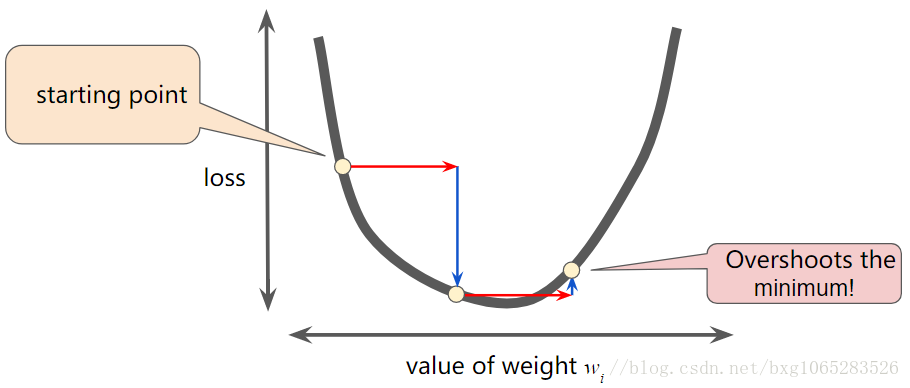
每一个回归问题都有一个理想的学习速率，它取决于误差函数的平滑程度，当知道梯度过小，可以谨慎的增大梯度，不可增加过大。

Key Terms

hyperparameter  超参数	learning rate学习速率
step size步长

4.Stochastic gradient descent（随机梯度下降法）

       在梯度下降法中，批量指的是用于在单次迭代中计算梯度的样本总数。到目前为止，我们一直假定批量是指整个数据集。如果是超大批量，则单次迭代就可能要花费很长时间进行计算。包含随机抽样样本的大型数据集可能包含冗余数据。实际上，批量大小越大，出现冗余的可能性就越高。一些冗余可能有助于消除杂乱的梯度，但超大批量所具备的预测价值往往并不比大型批量高。

通过从我们的数据集中随机选择样本，我们可以通过小得多的数据集估算（尽管过程非常杂乱）出较大的平均值。 随机梯度下降法 (SGD  Stochastic gradient descent) 将这种想法运用到极致，它每次迭代只使用一个样本（批量大小为 1）。如果进行足够的迭代，SGD 也可以发挥作用，但过程会非常杂乱。

小批量随机梯度下降法（mini-batch SGD）是介于全批量迭代与 SGD 之间的折衷方案。小批量通常包含 10-1000 个随机选择的样本。小批量 SGD 可以减少 SGD 中的杂乱样本数量，但仍然比全批量更高效。梯度下降法对于多特征的特征集同样有效。

Key Terms

batch 批量	batch size 批量大小
mini-batch小批量	stochastic gradient descent 随机梯度下降法