理解逻辑回归

最近研究了一下逻辑回归，阅读了相关代码和文章，对这块的知识有了一个比较全面的认识，于是准备边梳理边写下来，作为以后的备忘吧^_^

一、从线性回归开始
其实，逻辑回归本质上也是一种线性回归（所以它是线性的模型），只是线性回归用于回归或者说拟合，而逻辑回归是用来分类。

线性回归是假设

$$y = \theta_{i}x_{i} + \theta_{i-1}x_{i-1} + ... + \theta_{1}x_{1} + \theta_{0}　　(1)$$ 如果把 $\theta$和 $x$看作是(列)向量，那么用矩阵的形式可以简写成 $y = \theta^Tx$，然后根据样本去计算最适合的向量 $\theta$。

逻辑回归跟线性回归的不同点在于，他令

$$y = \frac {1} {1 + e^{-(\theta_{i}x_{i} + \theta_{i-1}x_{i-1} + ... + \theta_{1}x_{1} + \theta_{0})}} 　　即　　y = \frac {1} {1 + e^{-\theta^Tx}}　　(2)$$

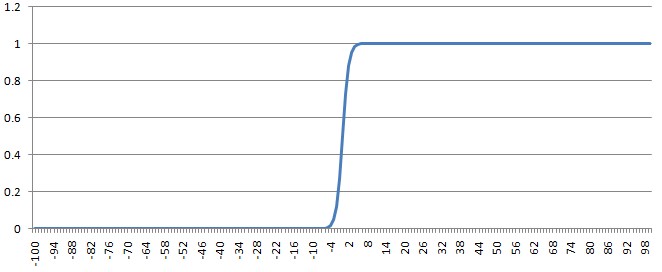
也就是说，使公式(1)又过了一下$\frac {1} {1 + e^{-t}}$函数，就是所谓的逻辑函数，也就是逻辑回归名字的由来。它的形态是这样的

至于为什么使用这个函数，涉及到一些数学方面的推导，等以后再写。现在只需要知道，公式(1)的取值范围是正负无穷大，而公式(2)的把这个取值压缩到了(0, 1)，考虑到逻辑回归所应用的二分类问题，这正好表示了某个样本属于1的概率。可以看到，如果公式(1)算出来的值很大或很小，那么分类就很好确定，而逻辑函数的性质正好解决了公式(1)取值在0附近的分类问题。

二、最小二乘法
那么，公式(1)或者公式(2)怎么求解$\theta$呢，我们从简单入手，看看怎么解决公式(1)，不妨再简化些，我们假设要求解的模型只有一个特征，即$y = \theta_{1}x + \theta_{0}$，然后用经典的最小二乘法（也叫最小误差平方）来求解。

假设样本集合为$(x_0, y_0)(x_1, y_1)...(x_m, y_m)$，那么我们的目的是要选择$\theta_{1}, \theta_{0}$使得下式的值最小

$$\sum (\theta_{1}x_i + \theta_{0} - y_i)^2$$

这个式子就是所谓的损失函数(loss function)，要想得到其最小值时的$\theta_{1}, \theta_{0}$，则需要分别对$\theta_{1}, \theta_{0}$求偏导，并令其导数为0。

$$2\sum (\theta_{1}x_i + \theta_{0} - y_i) = 0$$
$$2\sum (\theta_{1}x_i + \theta_{0} - y_i)x_i = 0$$
解这个方程组，得到
$$\theta_{0} = \frac {\sum x_{i}^2\sum y_{i} - \sum x_{i} \sum x_{i}y_{i}}{m\sum x_{i}^2 - (\sum x_{i})^2}$$
$$\theta_{1} = \frac {m\sum x_{i}y_{i} - \sum x_{i} \sum y_{i}}{m\sum x_{i}^2 - (\sum x_{i})^2}$$

所有的$x_{i}, y_{i}$是我们的训练集合，求解$\theta_{1}, \theta_{0}$的代码如下

def LeastSquare(x_list, y_list):
    m = len(x_list)
    t1 = t2 = t3 = t4 = 0
    for i in range(data_num):
        t1 += x_list[i]
        t2 += y_list[i]
        t3 += x_list[i] ** 2
        t4 += x_list[i] * y_list[i]

    theta0 = (t3*t2 - t1*t4)/(m*t3 - t1*t1)
    theta1 = (m*t4 - t1*t2)/(m*t3 - t1*t1)
    return theta0, theta1

三、梯度下降法
可以看到，在上述简化的不能再简化的线性模型上（只有一个特征，参数只有$\theta_{1}, \theta_{0}$两个），是可以通过数学的方法求得最优解的。但如果问题稍微复杂一些，比如有很多个特征（相应的，参数也随之递增）的时候，损失函数就变成这个样子

$$\sum ( \theta_{i}x_{i} + \theta_{i-1}x_{i-1} + ... + \theta_{1}x_{1} + \theta_{0} - y_i)^2　　(3)$$
如果想要对每个 $\theta$分量求偏导，然后令导数为0并建立方程组的话，不一定有解；就算有，解起来也是非常困难的，并且不具有扩展性（比如引入了新的特征）。

所以，人们引入了梯度下降法解决这类问题。它的基本原理是，损失函数是关于各个$\theta$分量的函数，想要求得使损失函数最小的各个$\theta$分量，就要让每个$\theta$分量沿着其梯度的方向不断的前进，最终达到一个稳定的状态，此时的$\theta$就是使得损失函数最小（严格的说，是局部最小）的$\theta$。

那么，用公式(3)对每个$\theta$分量求偏导得到

$$2\sum ( \theta_{i}x_{i} + \theta_{i-1}x_{i-1} + ... + \theta_{1}x_{1} + \theta_{0} - y_i)x_{i}　　即　　2\sum ( \theta^Tx - y_i)x_{i}$$
这就是每个 $\theta$分量的梯度，每次迭代时需要用当前的 $\theta$减去这个梯度，形成新的 $\theta$。这个梯度可以通俗的描述成： $\sum (当前\theta算出的预测值与实际值的差) × 特征i的值$

四、回到逻辑回归
实际上，线性回归的损失函数为公式(3)，那么逻辑回归的损失函数自然可以写成（为了求导方便在前面乘了个$\frac{1}{2}$）

$$\frac{1}{2}\sum(\frac{1}{1+e^{-\theta^Tx}}-y_{i})^2$$
对 $\theta$求偏导，得到梯度如下
$$\sum ( \frac{1}{1+e^{-\theta^Tx}}-y_{i})(\frac {1}{e^{-\theta^{T}x} + e^{\theta^{T}x} + 2})x_{i}$$

声明：这里说的是一个错误的方向，但却是我在理解逻辑回归过程中的一个自然而然的思考方向，希望我的导数没有求错，其实正确的梯度是这样子滴

$$-\sum (y_{i} - \frac{1}{1+e^{-\theta^Tx}})x_{i}　　(4)$$

究竟孰是孰非呢，so let code win arguments，于是，构造数据集和测试集，实际验证一下逻辑回归的分类方法

build_test.py

#-*- coding:utf-8 -*-
from numpy import *

weights = []

m = 100000      #测试集数量
ms = 10000      #训练集数量
n = 1000        #特征数

for i in range(n+1):    #随机生成权重，注意n+1是因为还有个常数项，即w0
    weights.append(random.uniform(-100,100))

def sigmoid(x):
    return 1 / (1 + exp(-x))

featureDet = []
for i in range(m):
    featureList = []
    for j in range(n):
            featureList.append(random.uniform(-10,10))#随机生成各特征值，都在统一范围，不用归一化
    featureList.append(1.0)#最后加个1，去乘常数项
    label = 0
    if (sigmoid(mat(featureList) * mat(weights).transpose()) > 0.5):
        label = 1
    featureList.insert(0, label)#每行的格式：label feature1 feature2 ...

    del featureList[-1]#输出的时候，把最后的1去掉
    featureDet.append(featureList)

fp = open("test.txt", "w")
for i in range(m):
    for j in range(n+1):
        fp.write(str(featureDet[i][j]) + " ")
    fp.write("\n")
fp.close()

fp = open("sample.txt", "w")
for i in range(ms):
    for j in range(n+1):
        fp.write(str(featureDet[i][j]) + " ")
    fp.write("\n")
fp.close()

train.py

# -*- utf-8 -*-
from numpy import *
import sys
import time

def LoadDataSet(dataFile):
    featureDet = []
    labelDet = []

    fp = open(dataFile, "r")

    for line in fp.readlines():
        lineArr = line.strip().split()
        featureList = []
        for i in range(1, len(lineArr)):
            featureList.append(float(lineArr[i]))
        featureList.append(1.0)

        featureDet.append(featureList)

        labelDet.append(float(lineArr[0]))

    fp.close()

    return featureDet, labelDet

def sigmoid(x):
    return 1 / (1 + exp(-x))

def Train(featureDet, labelDet):#正确的梯度训练
    featureMat = mat(featureDet)
    labelMat = mat(labelDet).transpose()

    m,n = shape(featureMat)
    alpha = 0.001
    maxCycle = 500
    weights = ones((n, 1))

    for i in range(maxCycle):
        h = sigmoid(featureMat * weights)
        error = h - labelMat
        weights = weights - alpha * featureMat.transpose() * error

    return weights

def Test(x):
    return 1 / (exp(-x) + exp(x) + 2)

def TrainTest(featureDet, labelDet):#错误的梯度训练
    featureMat = mat(featureDet)
    labelMat = mat(labelDet).transpose()

    m,n = shape(featureMat)
    alpha = 0.001
    maxCycle = 500
    weights = ones((n, 1))

    for i in range(maxCycle):
        h = sigmoid(featureMat * weights)
        error = h - labelMat
        t = Test(featureMat * weights)#这行的处理是两个梯度的不同之处
        weights = weights - alpha * featureMat.transpose() * multiply(error, t)

    return weights

def LabelMap(x):
    if (x > 0.5):
        return 1
    return 0

def GetErrorRate(featureDet, labelDet, weights):
    predict_label = sigmoid(mat(featureDet) * weights)
    error_count = 0.0
    for i in range(len(labelDet)):
        if LabelMap(predict_label[i][0]) != int(labelDet[i]):
            error_count += 1

    return error_count/len(labelDet)

def main():
    if len(sys.argv) != 3:
        print "Usage: %s <training_set_file> <testing_set_file>" % (sys.argv[0])
        sys.exit(-1)
    print "Load file ..." 
    featureDet, labelDet = LoadDataSet(sys.argv[1])
    featureDetTest, labelDetTest = LoadDataSet(sys.argv[2])
    print "ok"

    print "Training ..."
    time1 = time.time()
    weights = Train(featureDet, labelDet)
    time2 = time.time()
    error_rate = GetErrorRate(featureDetTest, labelDetTest, weights)
    print "ok\nErrorRate: %f\tTime: %d\n" % (error_rate, time2-time1)

    print "TrainingTest ..."
    time1 = time.time()
    weights = TrainTest(featureDet, labelDet)
    time2 = time.time()
    error_rate = GetErrorRate(featureDetTest, labelDetTest, weights)
    print "ok\nErrorRate: %f\tTime: %d\n" % (error_rate, time2-time1)

main()

运行如下

# python build_test.py
# python train.py .sample.txt .test.txt 
Load file ...
ok
Training ...
ok
ErrorRate: 0.046490     Time: 84

TrainingTest ...
ok
ErrorRate: 0.491450     Time: 91

结果已经说明问题，错误梯度的预测结果一团糟，到底是哪里出了问题？

四、逻辑回归的损失函数和梯度
其实问题就出在了：上一节中逻辑回归所使用的损失函数不对，自然其梯度也是错误的。那么为什么线性回归可以使用最小二乘作为损失函数，而与其一脉相承的逻辑回归就不行哩？
我本人是通过一个例子来理解这个问题的（不一定准确，理论推导以后再说），假设有三个样本，类别分别为1,1,0，模型1预测结果为0.6,0.6,0.4，模型2预测结果为0.9,0.9,0.6，由于模型1全部分类正确，而模型2分错了一个，前者优于后者。但是模型1的最小二乘为0.16+0.16+0.16=0.48，模型2的最小二乘为0.01+0.01+0.36=0.38，后者却小于前者，与实际的结论产生矛盾。
还有从另外一个角度来解释就是，$\frac{1}{2}\sum(\frac{1}{1+e^{-\theta^Tx}}-y_{i})^2$这个函数由于包含了sigmoid函数，所以它不是凸函数，没有最优解。

下面从概率的角度推导出逻辑回归损失函数的正确形式，因为逻辑回归每个样本的目标值y只能取0、1两个值，所以每个样本的目标值概率符合两项分布（伯努利分布），即$P(y=1|x) = p^{y}\cdot(1-p)^{1-y}$，而其中的$p$，公式(2)及其后面的说明已经给出$p = \frac {1} {1 + e^{-\theta^Tx}}$

每个样本都是独立的，所以样本集的联合概率分布为：

$$\prod_{i=1}^{m} (\frac {1} {1 + e^{-\theta^Tx}})^{y_i}\cdot(\frac {e^{-\theta^Tx}} {1 + e^{-\theta^Tx}})^{1-y_i}$$
为了计算简便，取自然对数变成加和形式
$$\sum y_{i}ln(\frac {1} {1 + e^{-\theta^Tx}}) + (1-y_{i})ln(\frac {e^{-\theta^Tx}} {1 + e^{-\theta^Tx}})$$
$$\sum y_{i}ln(\frac {1} {1 + e^{-\theta^Tx}}) + (1-y_{i})ln(\frac {1} {1 + e^{\theta^Tx}})$$
$$\sum -y_{i}ln(1 + e^{-\theta^Tx}) -ln(1 + e^{\theta^Tx}) + y_{i}ln(1 + e^{\theta^Tx})$$
$$\sum y_{i}ln(\frac{1 + e^{\theta^Tx}}{1 + e^{-\theta^Tx}}) - ln(1 + e^{\theta^Tx})$$
$$\sum y_{i} (\theta^Tx) - ln(1 + e^{\theta^Tx})$$
对 $\theta$求导得到梯度为
$$\sum (y_{i} - \frac {1} {1 + e^{-\theta^Tx}})x_{i}$$
而因为，这里的损失函数是概率，所以目标是要使其最大化，也就是求最大值，所以需要沿着负梯度的方向迭代，就是所谓的梯度上升了。如果要与梯度下降的说法保持一致（即让 $\theta$每次 减去梯度），则需要在前面加一个负号
$$-\sum (y_{i} - \frac {1} {1 + e^{-\theta^Tx}})x_{i}$$
就是前面所说的公式(4)了