【Codeforces 364E】Empty Rectangle

给一个$n\ast m$的01矩阵，求其中恰含$K$个1的子矩阵的方案数。
$1\le n,m\le 2500,0\le K\le 6$

---

做这个题时完全没有往分治的方向想。
面对这种矩阵的分治，不妨像K-D Tree那样行列交替切割。边界条件很容易确定。
这样一来，恰位于两半边的子矩阵全部处理完毕，考虑处理跨过切割线的子矩阵（以横着切割为例）。

我们枚举子矩阵的左右两端点（分别记作$i,j$），令$f[0][k]$为矩形$[(f[0][k],i),(mid,j)]$满足其1的个数小于k的最小纵坐标，$f[1][k]$为矩形$[(i,mid+1),(f[1][k],j)]$满足其1的个数小于k的最大纵坐标。则该情形下的答案为：
$$\sum _{k=0}^K(f[0][k]-f[0][k+1])\ast (f[1][K-k+1][K-k])$$

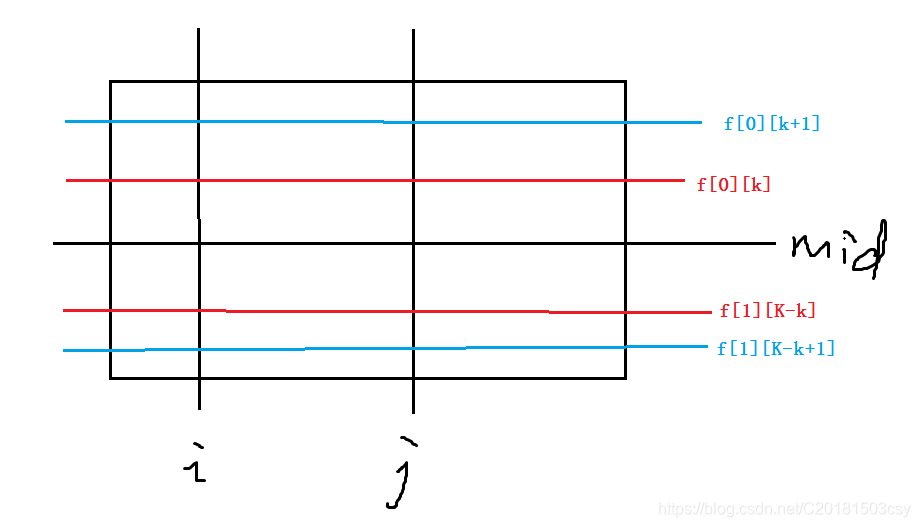
考虑如何求$f$。发现当$i$固定时，$f[0],f[1]$均有单调性。于是，每一次移动$j$时，依次更新$f$中的元素即可。
枚举$i,j$的复杂度为$O(n^2)$或$O(m^2)$，故处理一次切割线上的信息为$O(nmk)$，总的时间复杂度为$O(nmk{\log }_{2}n)$。

---

#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int mn = 2505;
int a[mn][mn], n, m, K;
char s[mn];
ll f[2][10], ans;
inline int num(int x1, int y1, int x2, int y2) {return a[x2][y2] - a[x1][y2] - a[x2][y1] + a[x1][y1];}
void solve(int x1, int y1, int x2, int y2, bool flg)
{
    if(x1 == x2 || y1 == y2) return;
    if(x1 + 1 == x2 && y1 + 1 == y2) {ans += (num(x1, y1, x2, y2) == K); return;}
    if(flg)
    {
        int mid = (x1 + x2) >> 1;
        solve(x1, y1, mid, y2, 0), solve(mid, y1, x2, y2, 0);
        for(int i = y1; i < y2; i++)
        {
            f[0][0] = f[1][0] = mid;
            for(int j = 1; j <= K + 1; j++)
                f[0][j] = x1, f[1][j] = x2;
            for(int j = i + 1; j <= y2; j++)
            {
                for(int k = 1; k <= K + 1; k++)
                {
                    while(num(f[0][k], i, mid, j) >= k) ++f[0][k];
                    while(num(mid, i, f[1][k], j) >= k) --f[1][k];
                }
                for(int k = 0; k <= K; k++)
                    ans += (f[0][k] - f[0][k + 1]) * (f[1][K - k + 1] - f[1][K - k]);
            }
        }
    }
    else
    {
        int mid = (y1 + y2) >> 1;
        solve(x1, y1, x2, mid, 1), solve(x1, mid, x2, y2, 1);
        for(int i = x1; i < x2; i++)
        {
            f[0][0] = f[1][0] = mid;
            for(int j = 1; j <= K + 1; j++)
                f[0][j] = y1, f[1][j] = y2;
            for(int j = i + 1; j <= x2; j++)
            {
                for(int k = 1; k <= K + 1; k++)
                {
                    while(num(i, f[0][k], j, mid) >= k) ++f[0][k];
                    while(num(i, mid, j, f[1][k]) >= k) --f[1][k];
                }
                for(int k = 0; k <= K; k++)
                    ans += (f[0][k] - f[0][k + 1]) * (f[1][K - k + 1] - f[1][K - k]);
            }
        }
    }
}
int main()
{
    scanf("%d%d%d", &n, &m, &K);
    for(int i = 1; i <= n; i++)
    {
        scanf("%s", s + 1);
        for(int j = 1; j <= m; j++)
            a[i][j] = s[j] - '0', a[i][j] += a[i-1][j] + a[i][j-1] - a[i-1][j-1];
    }
    solve(0, 0, n, m, 0);
    printf("%I64d\n", ans);
}