手把手教你写一个生成对抗网络

成对抗网络代码全解析, 详细代码解析(TensorFlow, numpy, matplotlib, scipy)

那么，什么是 GANs？

用 Ian Goodfellow 自己的话来说：

“生成对抗网络是一种生成模型（Generative Model），其背后基本思想是从训练库里获取很多训练样本，从而学习这些训练案例生成的概率分布。

而实现的方法，是让两个网络相互竞争，‘玩一个游戏’。其中一个叫做生成器网络（ Generator Network），它不断捕捉训练库里真实图片的概率分布，将输入的随机噪声（Random Noise）转变成新的样本（也就是假数据）。另一个叫做判别器网络（Discriminator Network），它可以同时观察真实和假造的数据，判断这个数据到底是不是真的。”

对不熟悉 GANs 的读者，这番解释或许有些晦涩。因此，雷锋网特地找来 AI 博主 Adit Deshpande 的解释，更加清楚直白：

“GANs 的基本原理是它有两个模型：一个生成器，一个判别器。判别器的任务是判断给定图像是否看起来‘自然’，换句话说，是否像是人为（机器）生成的。而生成器的任务是，顾名思义，生成看起来‘自然’的图像，要求与原始数据分布尽可能一致。

GANs 的运作方式可被看作是两名玩家之间的零和游戏。原论文的类比是，生成器就像一支造假币的团伙，试图用假币蒙混过关。而判别器就像是警察，目标是检查出假币。生成器想要骗过判别器，判别器想要不上当。当两组模型不断训练，生成器不断生成新的结果进行尝试，它们的能力互相提高，直到生成器生成的人造样本看起来与原始样本没有区别。”

更多“什么是 GANs ？”的详细解说，请参考雷锋网整理的 Ian Goodfellow  NIPS 大会 ppt 演讲，Yan Lecun 演讲，以及香港理工大学博士生李嫣然的 “GANs 最新进展”特约稿。

早期的 GANs 模型有许多问题。Yan Lecun 指出，其中一项主要缺陷是：GANs 不稳定，有时候它永远不会开始学习，或者生成我们认为合格的输出。这需要之后的研究一步步解决。

“生成对抗网络是一种生成模型（Generative Model），其背后基本思想是从训练库里获取很多训练样本，从而学习这些训练案例生成的概率分布。

今天我们接着上一讲“#9 生成对抗网络101 终极入门与通俗解析”， 手把手教你写一个生成对抗网络。参考代码是：https://github.com/AYLIEN/gan-intro

关键python库: TensorFlow, numpy, matplotlib, scipy

我们上次讲过，生成对抗网络同时训练两个模型, 叫做生成器和判断器. 生成器竭尽全力模仿真实分布生成数据; 判断器竭尽全力区分出真实样本和生成器生成的模仿样本. 直到判断器无法区分出真实样本和模仿样本为止.

来自：http://blog.aylien.com/introduction-generative-adversarial-networks-code-tensorflow/

上图是一个生成对抗网络的训练过程，我们所要讲解的代码就是要实现这样的训练过程。
其中， 绿色线的分布是一个高斯分布（真实分布），期望和方差都是固定值，所以分布稳定。红色线的分布是生成器分布，他在训练过程中与判断器对抗，不断改变分布模仿绿色线高斯分布. 整个过程不断模仿绿色线。蓝色线的分布就是判断器，约定为, 概率密度越高, 认为真实数据的可能性越大. 可以看到蓝线在真实数据期望4的地方,蓝色线概率密度越来越小, 即, 判断器难区分出生成器和判断器.

接下来我们来啃一下David 9看过最复杂的TensorFlow源码逻辑:

首先看总体逻辑:

来自: https://ishmaelbelghazi.github.io/ALI

正像之前所说, 有两个神经模型在交替训练. 生成模型输入噪声分布, 把噪声分布映射成很像真实分布的分布, 生成仿造的样本. 判断模型输入生成模型的仿造样本, 区分这个样本是不真实样本. 如果最后区分不出, 恭喜你, 模型训练的很不错.

我们的生成器模型映射作用很像下图:

Z是一个平均分布加了点噪声而已.  X是真实分布. 我们希望这个神经网络输入相同间隔的输入值 , 输出就能告诉我们这个值的概率密度(pdf)多大? 很显然-1这里pdf应该比较大.

Z如何写代码? 很简单:

1. classGeneratorDistribution(object):
2. def __init__(self,range):
3. self.range = range
5. def sample(self,N):
6. return np.linspace(-self.range, self.range,N) + \
7. np.random.random(N) * 0.01

查不多采样值像下图:

只是多了一点点噪声而已.

生成器用一层线性, 加一层非线性, 最后加一层线性的神经网络.

判断器需要强大一些, 用三层线神经网络去做:

1. def discriminator(input, hidden_size):
2. h0 = tf.tanh(linear(input, hidden_size * 2,'d0'))
3. h1 = tf.tanh(linear(h0, hidden_size * 2,'d1'))
4. h2 = tf.tanh(linear(h1, hidden_size * 2,'d2'))
5. h3 = tf.sigmoid(linear(h2,1,'d3'))
6. return h3

然后, 我们构造TensorFlow图, 还有判断器和生成器的损失函数:

1. with tf.variable_scope('G'):
2. z = tf.placeholder(tf.float32, shape=(None,1))
3. G = generator(z, hidden_size)
5. with tf.variable_scope('D')as scope:
6. x = tf.placeholder(tf.float32, shape=(None,1))
7. D1 = discriminator(x, hidden_size)
8. scope.reuse_variables()
9. D2 = discriminator(G, hidden_size)
11. loss_d = tf.reduce_mean(-tf.log(D1) - tf.log(1 - D2))
12. loss_g = tf.reduce_mean(-tf.log(D2))

最神奇的应该是这句:

1. loss_d = tf.reduce_mean(-tf.log(D1) - tf.log(1 - D2))

我们有同样的一个判断模型, D1和D2的区别仅仅是D1的输入是真实数据, D2的输入是生成器的伪造数据. 注意, 代码中判断模型的输出是“认为一个样本在真实分布中的可能性”. 所以优化时目标是, D1的输出要尽量大, D2的输出要尽量小.

此外, 优化生成器的时候, 我们要欺骗判断器, 让D2的输出尽量大:

1. loss_g = tf.reduce_mean(-tf.log(D2))

最难的难点, David 9 给大家已经讲解了. 如何写优化器(optimizer)和训练过程, 请大家参考源代码~

源代码:

1. '''
2. An example of distribution approximation using Generative Adversarial Networks in TensorFlow.
4. Based on the blog post by Eric Jang: http://blog.evjang.com/2016/06/generative-adversarial-nets-in.html,
5. and of course the original GAN paper by Ian Goodfellow et. al.: https://arxiv.org/abs/1406.2661.
7. The minibatch discrimination technique is taken from Tim Salimans et. al.: https://arxiv.org/abs/1606.03498.
8. '''
9. from __future__ import absolute_import
10. from __future__ import print_function
11. from __future__ import unicode_literals
12. from __future__ import division
14. import argparse
15. import numpy as np
16. from scipy.statsimport norm
17. import tensorflow as tf
18. import matplotlib.pyplotas plt
19. from matplotlib import animation
20. import seaborn as sns
22. sns.set(color_codes=True)
24. seed =42
25. np.random.seed(seed)
26. tf.set_random_seed(seed)
29. classDataDistribution(object):
30. def __init__(self):
31. self.mu = 4
32. self.sigma = 0.5
34. def sample(self,N):
35. samples = np.random.normal(self.mu, self.sigma,N)
36. samples.sort()
37. return samples
40. classGeneratorDistribution(object):
41. def __init__(self,range):
42. self.range = range
44. def sample(self,N):
45. return np.linspace(-self.range, self.range,N) + \
46. np.random.random(N) * 0.01
49. def linear(input, output_dim, scope=None, stddev=1.0):
50. norm = tf.random_normal_initializer(stddev=stddev)
51. const = tf.constant_initializer(0.0)
52. with tf.variable_scope(scopeor'linear'):
53. w = tf.get_variable('w',[input.get_shape()[1], output_dim], initializer=norm)
54. b = tf.get_variable('b',[output_dim], initializer=const)
55. return tf.matmul(input, w) + b
58. def generator(input, h_dim):
59. h0 = tf.nn.softplus(linear(input, h_dim, 'g0'))
60. h1 = linear(h0,1,'g1')
61. return h1
64. def discriminator(input, h_dim, minibatch_layer=True):
65. h0 = tf.tanh(linear(input, h_dim * 2,'d0'))
66. h1 = tf.tanh(linear(h0, h_dim * 2,'d1'))
68. # without the minibatch layer, the discriminator needs an additional layer
69. # to have enough capacity to separate the two distributions correctly
70. if minibatch_layer:
71. h2 = minibatch(h1)
72. else:
73. h2 = tf.tanh(linear(h1, h_dim * 2, scope='d2'))
75. h3 = tf.sigmoid(linear(h2,1, scope='d3'))
76. return h3
79. def minibatch(input, num_kernels=5, kernel_dim=3):
80. x = linear(input, num_kernels * kernel_dim, scope='minibatch', stddev=0.02)
81. activation = tf.reshape(x,(-1, num_kernels, kernel_dim))
82. diffs = tf.expand_dims(activation,3) - tf.expand_dims(tf.transpose(activation,[1,2,0]),0)
83. eps = tf.expand_dims(np.eye(int(input.get_shape()[0]), dtype=np.float32),1)
84. abs_diffs = tf.reduce_sum(tf.abs(diffs),2) + eps
85. minibatch_features = tf.reduce_sum(tf.exp(-abs_diffs),2)
86. return tf.concat(1,[input, minibatch_features])
89. def optimizer(loss, var_list):
90. initial_learning_rate =0.005
91. decay =0.95
92. num_decay_steps =150
93. batch = tf.Variable(0)
94. learning_rate = tf.train.exponential_decay(
95. initial_learning_rate,
96. batch,
97. num_decay_steps,
98. decay,
99. staircase=True
100. )
101. optimizer = tf.train.GradientDescentOptimizer(learning_rate).minimize(
102. loss,
103. global_step=batch,
104. var_list=var_list
105. )
106. return optimizer
109. classGAN(object):
110. def __init__(self, data, gen, num_steps, batch_size, minibatch, log_every, anim_path):
111. self.data = data
112. self.gen = gen
113. self.num_steps = num_steps
114. self.batch_size = batch_size
115. self.minibatch = minibatch
116. self.log_every = log_every
117. self.mlp_hidden_size = 4
118. self.anim_path = anim_path
119. self.anim_frames = []
120. self._create_model()
122. def _create_model(self):
123. # In order to make sure that the discriminator is providing useful gradient
124. # information to the generator from the start, we're going to pretrain the
125. # discriminator using a maximum likelihood objective. We define the network
126. # for this pretraining step scoped as D_pre.
127. with tf.variable_scope('D_pre'):
128. self.pre_input = tf.placeholder(tf.float32, shape=(self.batch_size,1))
129. self.pre_labels = tf.placeholder(tf.float32, shape=(self.batch_size,1))
130. D_pre = discriminator(self.pre_input, self.mlp_hidden_size, self.minibatch)
131. self.pre_loss = tf.reduce_mean(tf.square(D_pre - self.pre_labels))
132. self.pre_opt = optimizer(self.pre_loss,None)
134. # This defines the generator network - it takes samples from a noise
135. # distribution as input, and passes them through an MLP.
136. with tf.variable_scope('G'):
137. self.z = tf.placeholder(tf.float32, shape=(self.batch_size,1))
138. self.G = generator(self.z, self.mlp_hidden_size)
140. # The discriminator tries to tell the difference between samples from the
141. # true data distribution (self.x) and the generated samples (self.z).
142. #
143. # Here we create two copies of the discriminator network (that share parameters),
144. # as you cannot use the same network with different inputs in TensorFlow.
145. with tf.variable_scope('D')as scope:
146. self.x = tf.placeholder(tf.float32, shape=(self.batch_size,1))
147. self.D1 = discriminator(self.x, self.mlp_hidden_size, self.minibatch)
148. scope.reuse_variables()
149. self.D2 = discriminator(self.G, self.mlp_hidden_size, self.minibatch)
152. # Define the loss for discriminator and generator networks (see the original
153. # paper for details), and create optimizers for both
154. #self.pre_loss = tf.reduce_mean(tf.square(D_pre - self.pre_labels))
155. self.loss_d = tf.reduce_mean(-tf.log(self.D1) - tf.log(1 - self.D2))
156. self.loss_g = tf.reduce_mean(-tf.log(self.D2))
158. vars = tf.trainable_variables()
159. self.d_pre_params = [vfor v invarsif v.name.startswith('D_pre/')]
160. self.d_params = [vfor v invarsif v.name.startswith('D/')]
161. self.g_params = [vfor v invarsif v.name.startswith('G/')]
163. #self.pre_opt = optimizer(self.pre_loss, self.d_pre_params)
164. self.opt_d = optimizer(self.loss_d, self.d_params)
165. self.opt_g = optimizer(self.loss_g, self.g_params)
167. def train(self):
168. with tf.Session()as session:
169. tf.initialize_all_variables().run()
171. # pretraining discriminator
172. num_pretrain_steps =1000
173. for step inxrange(num_pretrain_steps):
174. d =(np.random.random(self.batch_size) - 0.5) * 10.0
175. labels = norm.pdf(d, loc=self.data.mu, scale=self.data.sigma)
176. pretrain_loss,_ = session.run([self.pre_loss, self.pre_opt],{
177. self.pre_input: np.reshape(d,(self.batch_size,1)),
178. self.pre_labels: np.reshape(labels,(self.batch_size,1))
179. })
180. self.weightsD = session.run(self.d_pre_params)
182. # copy weights from pre-training over to new D network
183. for i, v inenumerate(self.d_params):
184. session.run(v.assign(self.weightsD[i]))
186. for step inxrange(self.num_steps):
187. # update discriminator
188. x = self.data.sample(self.batch_size)
189. z = self.gen.sample(self.batch_size)
190. loss_d,_ = session.run([self.loss_d, self.opt_d],{
191. self.x: np.reshape(x,(self.batch_size,1)),
192. self.z: np.reshape(z,(self.batch_size,1))
193. })
195. # update generator
196. z = self.gen.sample(self.batch_size)
197. loss_g,_ = session.run([self.loss_g, self.opt_g],{
198. self.z: np.reshape(z,(self.batch_size,1))
199. })
201. if step % self.log_every ==0:
202. #pass
203. print('{}: {}\t{}'.format(step, loss_d, loss_g))
205. if self.anim_path:
206. self.anim_frames.append(self._samples(session))
208. if self.anim_path:
209. self._save_animation()
210. else:
211. self._plot_distributions(session)
213. def _samples(self, session, num_points=10000, num_bins=100):
214. '''
215. Return a tuple (db, pd, pg), where db is the current decision
216. boundary, pd is a histogram of samples from the data distribution,
217. and pg is a histogram of generated samples.
218. '''
219. xs = np.linspace(-self.gen.range, self.gen.range, num_points)
220. bins = np.linspace(-self.gen.range, self.gen.range, num_bins)
222. # decision boundary
223. db = np.zeros((num_points,1))
224. for i inrange(num_points// self.batch_size):
225. db[self.batch_size * i:self.batch_size * (i + 1)] = session.run(self.D1,{
226. self.x: np.reshape(
227. xs[self.batch_size * i:self.batch_size * (i + 1)],
228. (self.batch_size,1)
229. )
230. })
232. # data distribution
233. d = self.data.sample(num_points)
234. pd,_ = np.histogram(d, bins=bins, density=True)
236. # generated samples
237. zs = np.linspace(-self.gen.range, self.gen.range, num_points)
238. g = np.zeros((num_points,1))
239. for i inrange(num_points// self.batch_size):
240. g[self.batch_size * i:self.batch_size * (i + 1)] = session.run(self.G,{
241. self.z: np.reshape(
242. zs[self.batch_size * i:self.batch_size * (i + 1)],
243. (self.batch_size,1)
244. )
245. })
246. pg,_ = np.histogram(g, bins=bins, density=True)
248. return db, pd, pg
250. def _plot_distributions(self, session):
251. db, pd, pg = self._samples(session)
252. db_x = np.linspace(-self.gen.range, self.gen.range,len(db))
253. p_x = np.linspace(-self.gen.range, self.gen.range,len(pd))
254. f, ax = plt.subplots(1)
255. ax.plot(db_x, db, label='decision boundary')
256. ax.set_ylim(0,1)
257. plt.plot(p_x, pd, label='real data')
258. plt.plot(p_x, pg, label='generated data')
259. plt.title('1D Generative Adversarial Network')
260. plt.xlabel('Data values')
261. plt.ylabel('Probability density')
262. plt.legend()
263. plt.show()
265. def _save_animation(self):
266. f, ax = plt.subplots(figsize=(6,4))
267. f.suptitle('1D Generative Adversarial Network', fontsize=15)
268. plt.xlabel('Data values')
269. plt.ylabel('Probability density')
270. ax.set_xlim(-6,6)
271. ax.set_ylim(0,1.4)
272. line_db, = ax.plot([],[], label='decision boundary')
273. line_pd, = ax.plot([],[], label='real data')
274. line_pg, = ax.plot([],[], label='generated data')
275. frame_number = ax.text(
276. 0.02,
277. 0.95,
278. '',
279. horizontalalignment='left',
280. verticalalignment='top',
281. transform=ax.transAxes
282. )
283. ax.legend()
285. db, pd,_ = self.anim_frames[0]
286. db_x = np.linspace(-self.gen.range, self.gen.range,len(db))
287. p_x = np.linspace(-self.gen.range, self.gen.range,len(pd))
289. def init():
290. line_db.set_data([],[])
291. line_pd.set_data([],[])
292. line_pg.set_data([],[])
293. frame_number.set_text('')
294. return(line_db, line_pd, line_pg, frame_number)
296. def animate(i):
297. frame_number.set_text(
298. 'Frame: {}/{}'.format(i,len(self.anim_frames))
299. )
300. db, pd, pg = self.anim_frames[i]
301. line_db.set_data(db_x, db)
302. line_pd.set_data(p_x, pd)
303. line_pg.set_data(p_x, pg)
304. return(line_db, line_pd, line_pg, frame_number)
306. anim = animation.FuncAnimation(
307. f,
308. animate,
309. init_func=init,
310. frames=len(self.anim_frames),
311. blit=True
312. )
313. anim.save(self.anim_path, fps=30, extra_args=['-vcodec','libx264'])
316. def main(args):
317. model =GAN(
318. DataDistribution(),
319. GeneratorDistribution(range=8),
320. args.num_steps,
321. args.batch_size,
322. args.minibatch,
323. args.log_every,
324. args.anim
325. )
326. model.train()
329. def parse_args():
330. parser = argparse.ArgumentParser()
331. parser.add_argument('--num-steps',type=int, default=1200,
332. help='the number of training steps to take')
333. parser.add_argument('--batch-size',type=int, default=12,
334. help='the batch size')
335. parser.add_argument('--minibatch',type=bool, default=False,
336. help='use minibatch discrimination')
337. parser.add_argument('--log-every',type=int, default=10,
338. help='print loss after this many steps')
339. parser.add_argument('--anim',type=str, default=None,
340. help='name of the output animation file (default: none)')
341. return parser.parse_args()
344. if __name__ == '__main__':
345. '''
346. data_sample =DataDistribution()
347. d = data_sample.sample(10)
348. print(d)
349. '''
350. main(parse_args())

 

参考文献：

生成对抗网络是14年Goodfellow Ian在论文Generative Adversarial Nets中提出来的。 
记录下自己的理解，日后忘记了也能用于复习。 
原文地址： http://blog.csdn.net/sxf1061926959/article/details/54630462

生成模型和判别模型

理解对抗网络，首先要了解生成模型和判别模型。判别模型比较好理解，就像分类一样，有一个判别界限，通过这个判别界限去区分样本。从概率角度分析就是获得样本x属于类别y的概率，是一个条件概率P（y|x）.而生成模型是需要在整个条件内去产生数据的分布，就像高斯分布一样，他需要去拟合整个分布，从概率角度分析就是样本x在整个分布中的产生的概率，即联合概率P（xy）。具体可以参考博文http://blog.csdn.net/zouxy09/article/details/8195017或者这一篇http://www.cnblogs.com/jerrylead/archive/2011/03/05/1971903.html详细地阐述了具体的数学推理过程。

两个模型的对比详见，原文链接http://blog.csdn.net/wolenski/article/details/7985426

两个模型的对比

对抗网络思想

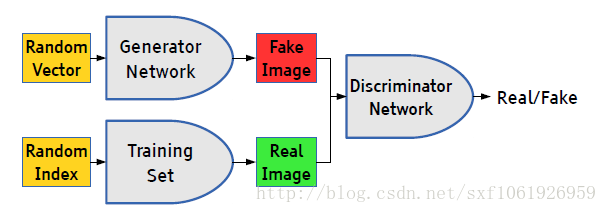
理解了生成模型和判别模型后，再来理解对抗网络就很直接了，对抗网络只是提出了一种网络结构，总体来说，整个框架还是很简单的。GANs简单的想法就是用两个模型，一个生成模型，一个判别模型。判别模型用于判断一个给定的图片是不是真实的图片（判断该图片是从数据集里获取的真实图片还是生成器生成的图片），生成模型的任务是去创造一个看起来像真的图片一样的图片，有点拗口，就是说模型自己去产生一个图片，可以和你想要的图片很像。而在开始的时候这两个模型都是没有经过训练的，这两个模型一起对抗训练，生成模型产生一张图片去欺骗判别模型，然后判别模型去判断这张图片是真是假，最终在这两个模型训练的过程中，两个模型的能力越来越强，最终达到稳态。（这里用图片举例，但是GANs的用途很广，不单单是图片，其他数据，或者就是简单的二维高斯也是可以的，用于拟合生成高斯分布。）

详细实现过程

下面我详细讲讲： 
假设我们现在的数据集是手写体数字的数据集minst。 
变量说明：初始化生成模型G、判别模型D（假设生成模型是一个简单的RBF，判别模型是一个简单的全连接网络，后面连接一层softmax（机器学习中常用的一种回归函数，详见https://www.zhihu.com/question/23765351）），样本为x，类别为y，这些都是假设，对抗网络的生成模型和判别模型没有任何限制。 

前向传播阶段

一、可以有两种输入 
1、我们随机产生一个随机向量作为生成模型的数据，然后经过生成模型后产生一个新的向量，作为Fake Image，记作D(z)。 
2、从数据集中随机选择一张图片，将图片转化成向量，作为Real Image,记作x。 
二、将由1或者2产生的输出，作为判别网络的输入，经过判别网络后输入值为一个0到1之间的数，用于表示输入图片为Real Image的概率，real为1，fake为0。 
使用得到的概率值计算损失函数，解释损失函数之前，我们先解释下判别模型的输入。根据输入的图片类型是Fake Image或Real Image将判别模型的输入数据的label标记为0或者1。即判别模型的输入类型为 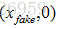或者 。

判别模型的损失函数：

 

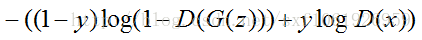
由于y为输入数据的类型，当输入的是从数据集中取出的real image数据时，y=1，上面公式的前半部分为0，只需考虑第二部分（后半部分）。又D(x)为判别模型的输出，表示输入x为real 数据（y=1，代表是real数据）的概率，我们的目的是让判别模型的输出D（x）的输出尽量靠近1。 

由于y为输入数据的类型，当输入的是从数据集中取出的fake image数据时，y=0，上面公式的后半部分为0，只需考虑第一部分（前半部分）。又因G（z）是生成模型的输出，输出的是一张Fake Image（y=0，表示输出的是fake数据）。我们要做的是让D(G(z))的输出尽可能趋向于0。这样才能表示判别模型是有区分力的。 

相对判别模型来说，这个损失函数其实就是交叉熵损失函数。计算loss，进行梯度反传。这里的梯度反传可以使用任何一种梯度修正的方法。 
当更新完判别模型的参数后，我们再去更新生成模型的参数。

给出生成模型的损失函数：

 
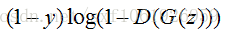
对于生成模型来说，我们要做的是让G（z）产生的数据尽可能的和数据集中的数据（真实的数据）一样。就是所谓的同样的数据分布。那么我们要做的就是最小化生成模型的误差，即只将由G（z）产生的误差传给生成模型。 
但是针对判别模型的预测结果，要对梯度变化的方向进行改变。当判别模型认为G（z）输出为真实数据集的时候和认为输出为噪声数据的时候，梯度更新方向要进行改变。 
即最终的损失函数为： 
 
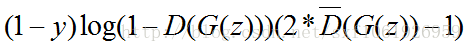
其中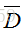表示判别模型的预测类别，对预测概率取整，为0或者1.用于更改梯度方向，阈值可以自己设置，或者正常的话就是0.5。

反向传播

我们已经得到了生成模型和判别模型的损失函数，这样分开看其实就是两个单独的模型，针对不同的模型可以按照自己的需要去实现不同的误差修正，我们也可以选择最常用的BP做为误差修正算法，更新模型参数。

其实说了这么多，生成对抗网络的生成模型和判别模型是没有任何限制，生成对抗网络提出的只是一种网络结构，我们可以使用任何的生成模型和判别模型去实现一个生成对抗网络。当得到损失函数后就按照单个模型的更新方法进行修正即可。

原文给了这么一个优化函数： 
看上去很难理解，我个人的理解是，它做的是要最大化D的区分度，最小化G和real数据集的数据分布。

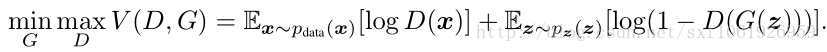
GoodFellow的论文证明了Gans 全局最小点的充分必要条件是:

pg表示generate 生成数据的分布函数 
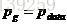
pdata表示真实data的分布函数

在训练过程中，pg不断地接近pdata,是收敛的判断标准。
我们知道，G和D是一个对抗的过程，而这个对抗是，G不断的学习，D也不断的学习，而且需要保证两者学习速率基本一致，也就是都能不断的从对方那里学习到“知识”来提升自己。否则，就是这两者哪一个学习的过快，或过慢，以至于双方的实力不再均衡，就会导致实力差的那一方的“loss”不再能“下降”，也就不在学到“知识”。一般的对抗模型中的G和D的网络框架大小基本上是相似(可能存在较小的差异)，而且，训练的过程就是先训练G一次，再训练D一次，这也是为了稳定训练的一个保证。当然这并不能完全稳定训练，所以，对抗网络的稳定训练，依然是一个研究的热点和方向。 
还有就是对抗网络当然依然很难生成分辨率大的但又不blurry的图片。从理论上来说也是很困难的事情，所以这个也是一个研究的目标。 

算法流程图

下图是原文给的算法流程，noise 就是随机输入生成模型的值。上面的解释加上这个图应该就能理解的差不多了。

noise输入的解释

上面那个noise也很好理解。如下图所示，假设我们现在的数据集是一个二维的高斯混合模型，那么这么noise就是x轴上我们随机输入的点，经过生成模型映射可以将x轴上的点映射到高斯混合模型上的点（将低维的映射为高维的）。当我们的数据集是图片的时候，那么我们输入的随机噪声其实就是相当于低维的数据，经过生成模型G的映射就变成了一张生成的图片G（x）。 
 
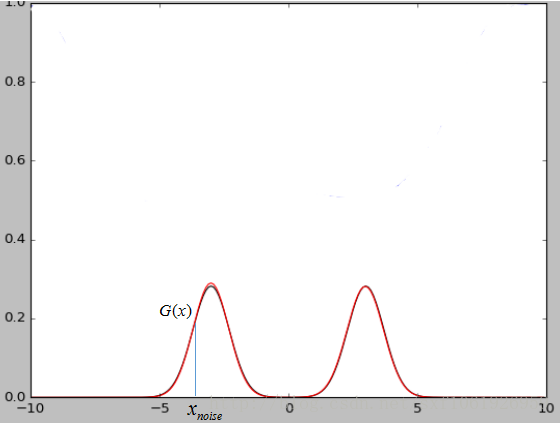
原文中也指出，最终两个模型达到稳态的时候判别模型D的输出接近1/2，也就是说判别器很难判断出图片是真是假，这也说明了网络是会达到收敛的。

GANs review

GANs一些新的应用方向在这篇博文中有所介绍，写的挺好： 
https://adeshpande3.github.io/adeshpande3.github.io/Deep-Learning-Research-Review-Week-1-Generative-Adversarial-Nets

*####################################################