ICLR 2023 | 中科大等提出分层序列模型，大幅提升数学规划求解效率

最新推荐文章于 2025-03-03 21:06:27 发布

PaperWeekly

最新推荐文章于 2025-03-03 21:06:27 发布

阅读量680

点赞数

原文链接：https://mp.weixin.qq.com/s?__biz=MzIwMTc4ODE0Mw==&mid=2247614286&idx=3&sn=f231261be8bd86db85a7eefa4b850b8a&chksm=96ebe0cea19c69d81fbaf1c788f48776d901314dc3f0db0d09ad1888dbb597f64414a11c20f5&scene=126&sessionid=0

版权

©来源 | 新智元

数学规划求解器因其重要性和通用性，被誉为运筹优化领域的「光刻机」。其中，混合整数线性规划 (Mixed-Integer Linear Programming, MILP) 是数学规划求解器的关键组件，可建模大量实际应用，如工业排产，物流调度，芯片设计，路径规划，金融投资等重大领域。

近期，中科大 MIRA Lab 王杰教授团队和华为诺亚方舟实验室联合提出分层序列模型（Hierarchical Sequence Model, HEM），大幅提升混合整数线性规划求解器求解效率，相关成果发表于 ICLR 2023。

目前，算法已整合入华为 MindSpore ModelZoo 模型库，相关技术和能力并将于今年内整合入华为天筹（OptVerse）AI 求解器。该求解器旨在将运筹学和AI相结合，突破业界运筹优化极限，助力企业量化决策和精细化运营，实现降本增效！

作者列表：

王治海*，李希君*，王杰**，匡宇飞，袁明轩，曾嘉，张勇东，吴枫

论文链接：

https://openreview.net/forum?id=Zob4P9bRNcK

开源数据集：

https://drive.google.com/drive/folders/1LXLZ8vq3L7v00XH-Tx3U6hiTJ79sCzxY?usp=sharing

PyTorch版本开源代码：

https://github.com/MIRALab-USTC/L2O-HEM-Torch

MindSpore版本开源代码：

https://gitee.com/mindspore/models/tree/master/research/l2o/hem-learning-to-cut

天筹（OptVerse）AI求解器：

https://www.huaweicloud.com/product/modelarts/optverse.html

▲ 图1. HEM 与求解器默认策略（Default）求解效率对比，HEM 求解效率最高可提升 47.28%

引言

平面（cutting planes, cuts）对于高效求解混合整数线性规划问题至关重要。其中割平面选择（cut selection）旨在选择待选割平面的恰当子集以提高求解 MILP 的效率。割平面选择在很大程度上取决于两个子问题：（P1）应优先选哪些割平面，以及（P2）应选择多少割平面。

尽管许多现代 MILP 求解器通过手动设计的启发式方法来处理 (P1) 和 (P2)，但机器学习方法有潜力学习更有效的启发式方法。然而，许多现有的学习类方法侧重于学习应该优先选择哪些割平面，而忽略了学习应该选择多少割平面。此外，我们从大量的实验结果中观察到又一子问题，即（P3）应该优先选择哪种割平面顺序，对求解 MILP 的效率也有重大影响。

为了应对这些挑战，我们提出了一种新颖的分层序列模型（Hierarchical Sequence Model, HEM），并通过强化学习框架来学习割平面选择策略。

据我们所知，HEM 是首个可同时处理（P1），（P2）和（P3）的学习类方法。实验表明，在人工生成和大规模真实世界 MILP 数据集上，与人工设计和学习类基线相比，HEM 大幅度提高了求解 MILP 的效率。

背景与问题介绍

2.1 割平面（cutting planes, cuts）介绍

混合整数线性规划（Mixed-Integer Linear Programming, MILP）是一种可广泛应用于多种实际应用领域的通用优化模型，例如供应链管理 [1]、排产规划 [2]、规划调度 [3]、工厂选址 [4]、装箱问题 [5] 等。

标准的 MILP 具有以下形式：

给定问题（1），我们丢弃其所有整数约束，可得到线性规划松弛（linear programming relaxation, LPR）问题，它的形式为：

由于问题（2）扩展了问题（1）的可行集，因此我们可有，即 LPR 问题的最优值是原 MILP 问题的下界。

给定（2）中的 LPR 问题，割平面（cutting planes, cuts）是一类合法线性不等式，这些不等式在添加到线性规划松弛问题中后，可收缩 LPR 问题中的可行域空间，且不去除任何原 MILP 问题中的整数可行解。

2.2 割平面选择（cut selection）介绍

MILP 求解器在求解 MILP 问题过程中可生成大量的割平面，且会在连续的回合中不断向原问题中添加割平面。具体而言，每一回合中包括五个步骤：

1. 求解当前的 LPR 问题；

2. 生成一系列待选割平面；

3. 从待选割平面中选择一个合适的子集；

4. 将选择的子集添加到 (1) 中的 LPR 问题，以得到一个新的 LPR 问题；

5. 循环重复，基于新的 LPR 问题，进入下一个回合。

将所有生成的割平面添加到 LPR 问题中可最大程度地收缩该问题的可行域空间，以最大程度提高下界。然而，添加过多的割平面可能会导致问题约束过多，增加问题求解计算开销并出现数值不稳定问题 [6,7]。

因此，研究者们提出了割平面选择（cut selection），割平面选择旨在选择候选割平面的适当子集，以尽可能提升 MILP 问题求解效率。割平面选择对于提高解决混合整数线性规划问题的效率至关重要 [8,9,10]。

2.3 启发实验——割平面添加顺序

我们设计了两种割平面选择启发式算法，分别为 RandomAll 和 RandomNV（详见原论文第 3 章节）。它们都在选择了一批割平面后，以随机顺序将选择的割平面添加到 MILP 问题中。如图 2 结果显示，选定同一批割平面的情况下，以不同的顺序添加这些选定割平面对求解器求解效率有极大的影响（详细结果分析见原论文第 3 章节）。

▲ 图2. 每一个柱子代表在求解器中，选定相同的一批割平面，以10轮不同的顺序添加这些选定割平面，求解器最终的求解效率的均值，柱子中的标准差线代表不同顺序下求解效率的标准差。标准差越大，代表顺序对求解器求解效率影响越大。

方法介绍

在割平面选择任务中，应该选择的最优子集是不可事先获取的。不过，我们可以使用求解器评估所选任意子集的质量，并以此评估作为学习算法的反馈。因此，我们利用强化学习（Reinforcement Learning, RL）范式来试错学习割平面选择策略。

在本节中，我们详细阐述了我们提出的 RL 框架。首先，我们将割平面选择任务建模为马尔科夫决策过程（Markov Decision Process, MDP）；然后，我们详细介绍我们提出的分层序列模型（hierarchical sequence model, HEM）；最后，我们推导可高效训练 HEM 的分层策略梯度。我们整体的 RL 框架图如图3所示。

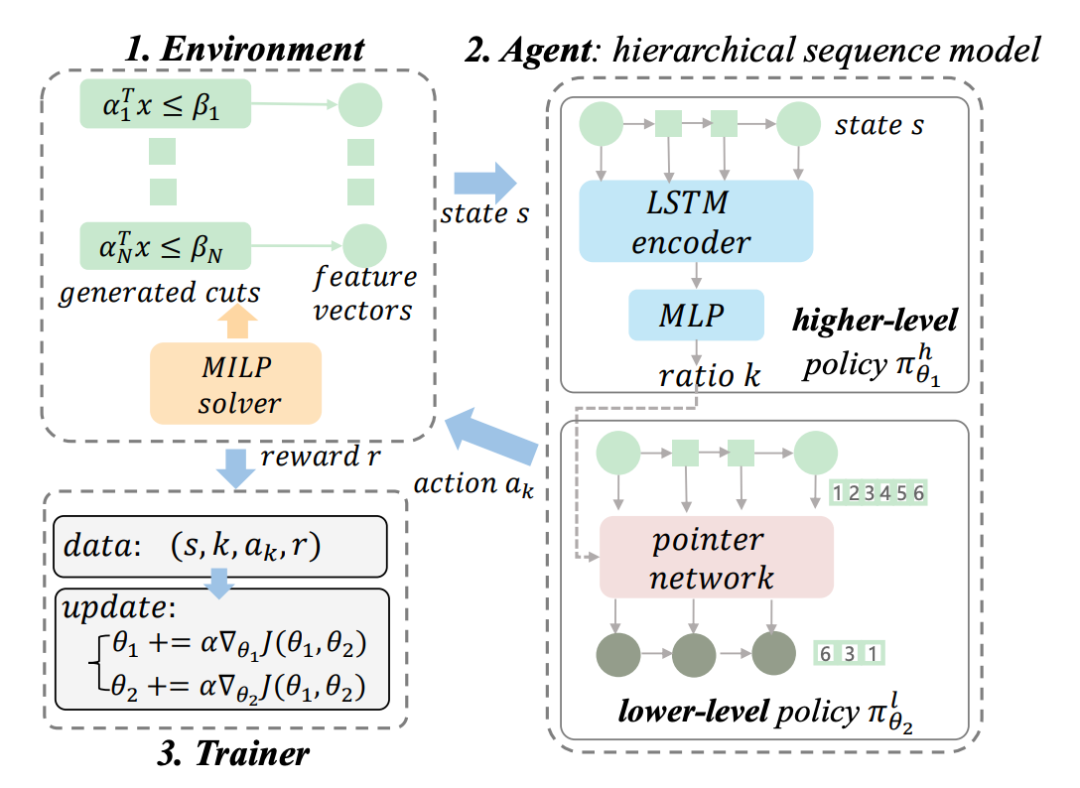
▲ 图3. 我们所提出的整体 RL 框架图。我们将 MILP 求解器建模为环境，将 HEM 模型建模为智能体。我们通过智能体和环境不断交互采集训练数据，并使用分层策略梯度训练 HEM 模型。

3.1 问题建模

状态空间：由于当前的 LP 松弛和生成的待选 cuts 包含割平面选择的核心信息，我们通过定义状态。这里表示当前 LP 松弛的数学模型，表示候选割平面的集合，表示 LP 松弛的最优解。为了编码状态信息，我们根据的信息为每个待选割平面设计 13 个特征。也就是说，我们通过一个 13 维特征向量来表示状态 s。具体细节请见原文第 4 章节。

动作空间：为了同时考虑所选 cut 的比例和顺序，我们以候选割平面集合的所有有序子集定义动作空间。

奖励函数：为了评估添加 cut 对求解 MILP 的影响，我们可通过求解时间，原始对偶间隙积分（primal-dual gap integral），对偶界提升（dual bound improvement）。具体细节请见原文第 4 章节。

转移函数：转移函数给定当前状态和采取的动作，输出下一状态。割平面选择任务中转移函数隐式地由求解器提供。

更多建模细节请见原文第 4 章节。

3.2 策略模型：分层序列模型

如图 3 所示，我们将 MILP 求解器建模为环境，将 HEM 建模为智能体，下面详细介绍所提出的 HEM 模型。为了方便阅读，我们简化方法动机，聚焦于讲清楚方法实现，欢迎感兴趣的读者参见原论文第 4 章节，了解相关细节。

如图 3 中 Agent 模块所示，HEM 由上下层策略模型组成。上下层模型分别学习上层策略（policy）和下层policy 。

首先，上层策略通过预测恰当的比例来学习应该选择的 cuts 的数量。假设状态长度为，预测比率为，那么预测应该选择的 cut 数为，其中表示向下取整函数。我们定义。

其次，下层策略学习选择给定大小的有序子集。下层策略可以定义，其中表示给定状态和比例的动作空间上的概率分布。具体来说，我们将下层策略建模为一个序列到序列模型（sequence to sequence model, sequence model）。

最后，通过全概率定律推导出 cut 选择策略，即：

3.3 训练方法：分层策略梯度

给定优化目标函数：

我们基于策略梯度定理 [11]，针对分层策略，推导出其适配的分层策略梯度，并以随机梯度下降的方式优化分层策略模型。如图 3 显示了分层策略梯度：

▲ 图4. 分层策略梯度。我们以此随机梯度下降的方式优化 HEM 模型

实验介绍

我们的实验有五个主要部分：

实验 1：在 3 个人工生成的 MILP 问题和来自不同应用领域的 6 个具有挑战性的 MILP 问题基准上评估我们的方法。

实验 2：进行精心设计的消融实验，以提供对 HEM 的深入洞察。

实验 3：测试 HEM 针对问题规模的泛化性能。

实验 4：可视化我们的方法与基线所选择的割平面特点。

实验 5：将我们的方法部署到华为实际的排产规划问题中，验证 HEM 的优越性。

我们在此文章中只介绍实验 1，更多实验结果，请参见原论文第 5 章节。请注意，我们论文中汇报的所有实验结果都是基于 PyTorch 版本代码训练得到的结果。

实验 1 结果如表 1 所示，我们在 9 个开源数据集上对比了 HEM 和 6 个基线的对比结果。实验结果显示，HEM 可平均提升约 20% 求解效率。

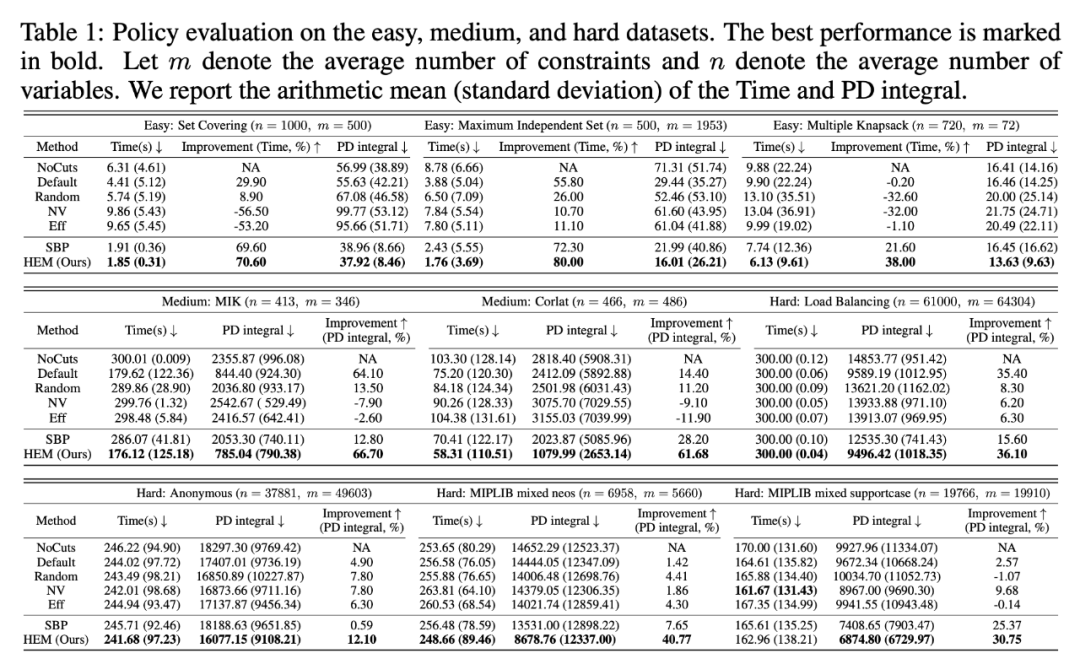
▲ 图5. 对easy、medium 和 hard 数据集的策略评估。最优性能我们用粗体字标出。以m表示约束条件的平均数量，n表示变量的平均数量。我们展示了求解时间和primal-dual gap 积分的算术平均值（标准偏差）。

参考文献

[1] Paschos, Vangelis Th, ed. Applications of combinatorial optimization. Vol. 3. John Wiley & Sons, 2014.

[2] Jünger, Michael, et al., eds. 50 Years of integer programming 1958-2008: From the early years to the state-of-the-art. Springer Science & Business Media, 2009.

[3] Chen, Zhi-Long. "Integrated production and outbound distribution scheduling: review and extensions." Operations research 58.1 (2010): 130-148.

[4] Farahani, Reza Zanjirani, and Masoud Hekmatfar, eds. Facility location: concepts, models, algorithms and case studies. Springer Science & Business Media, 2009.

[5] Nair, Vinod, et al. "Solving mixed integer programs using neural networks." arXiv preprint arXiv:2012.13349 (2020).

[6] Wesselmann, Franz, and U. Stuhl. "Implementing cutting plane management and selection techniques." Technical Report. University of Paderborn, 2012.

[7] Dey, Santanu S., and Marco Molinaro. "Theoretical challenges towards cutting-plane selection." Mathematical Programming 170 (2018): 237-266.

[8] Tang, Yunhao, Shipra Agrawal, and Yuri Faenza. "Reinforcement learning for integer programming: Learning to cut." International conference on machine learning. PMLR, 2020.

[9] Paulus, Max B., et al. "Learning to cut by looking ahead: Cutting plane selection via imitation learning." International conference on machine learning. PMLR, 2022.

[10] Huang, Zeren, et al. "Learning to select cuts for efficient mixed-integer programming." Pattern Recognition 123 (2022): 108353.

[11] Sutton, Richard S., and Andrew G. Barto. Reinforcement learning: An introduction. MIT press, 2018.

更多阅读