ICLR 2024 | 微软提出全新LLM剪枝方法：参数减少25%，大幅提升计算效率

最新推荐文章于 2025-03-17 17:58:34 发布

PaperWeekly

最新推荐文章于 2025-03-17 17:58:34 发布

阅读量1k

点赞数 1

文章标签：剪枝算法机器学习人工智能数据挖掘

原文链接：https://mp.weixin.qq.com/s?__biz=MzIwMTc4ODE0Mw==&mid=2247654180&idx=3&sn=14abc862869599074cf6db417a420b60&chksm=97960e0bfee3ceebe60b5fe0663b440495c4e8df30aae3460fc61a39964090abf46df05b19a3&scene=126&sessionid=0

版权

©作者 | 张倩、佳琪

来源 | 机器之心

删除权重矩阵的一些行和列，让 LLAMA-2 70B 的参数量减少 25%，模型还能保持 99% 的零样本任务性能，同时计算效率大大提升。这就是微软 SliceGPT 的威力。

大型语言模型（LLM）通常拥有数十亿的参数，用了数万亿 token 的数据进行训练，这样的模型训练、部署成本都非常高。因此，人们经常用各种模型压缩技术来减少它们的计算需求。

一般来讲，这些模型压缩技术可以分为四类：蒸馏、张量分解（包括低秩因式分解）、剪枝和量化。其中，剪枝方法已经存在了一段时间，但许多方法需要在剪枝后进行恢复微调（RFT）以保持性能，这使得整个过程成本高昂且难以扩展。

为了解决这一问题，来自苏黎世联邦理工学院、微软的研究者提出了一个名为 SliceGPT 的方法。SliceGPT 的核心思想是删除权重矩阵中的行和列来降低网络的嵌入维数，同时保持模型性能。

研究人员表示，有了 SliceGPT，他们只需几个小时就能使用单个 GPU 压缩大型模型，即使没有 RFT，也能在生成和下游任务中保持有竞争力的性能。目前，该论文已经被 ICLR 2024 接收。

论文标题：

SliceGPT: Compress Large Language Models by Deleting Rows and Columns

论文地址：

https://arxiv.org/pdf/2401.15024.pdf

剪枝方法的工作原理是将 LLM 中权重矩阵的某些元素设置为零，并（选择性地）更新矩阵的周围元素以进行补偿。其结果是形成了一种稀疏模式，这意味着在神经网络前向传递所需的矩阵乘法中，可以跳过一些浮点运算。

运算速度的相对提升取决于稀疏程度和稀疏模式：结构更合理的稀疏模式会带来更多的计算增益。与其他剪枝方法不同，SliceGPT 会剪掉（切掉！）权重矩阵的整行或整列。在切之前，他们会对网络进行一次转换，使预测结果保持不变，但允许剪切过程带来轻微的影响。

结果是权重矩阵变小了，神经网络块之间传递的信号也变小了：他们降低了神经网络的嵌入维度。

下图 1 将 SliceGPT 方法与现有的稀疏性方法进行了比较。

通过大量实验，作者发现 SliceGPT 可以为 LLAMA-2 70B、OPT 66B 和 Phi-2 模型去除多达 25% 的模型参数（包括嵌入），同时分别保持密集模型 99%、99% 和 90% 的零样本任务性能。

经过 SliceGPT 处理的模型可以在更少的 GPU 上运行，而且无需任何额外的代码优化即可更快地运行：在 24GB 的消费级 GPU 上，作者将 LLAMA-2 70B 的推理总计算量减少到了密集模型的 64%；在 40GB 的 A100 GPU 上，他们将其减少到了 66%。

此外，他们还提出了一种新的概念，即 Transformer 网络中的计算不变性（computational invariance），它使 SliceGPT 成为可能。

SliceGPT 详解

SliceGPT 方法依赖于 Transformer 架构中固有的计算不变性。这意味着，你可以对一个组件的输出应用一个正交变换，只要在下一个组件中撤销即可。作者观察到，在网络区块之间执行的 RMSNorm 运算不会影响变换：这些运算是可交换的。

在论文中，作者首先介绍了在 RMSNorm 连接的 Transformer 网络中如何实现不变性，然后说明如何将使用 LayerNorm 连接训练的网络转换为 RMSNorm。接下来，他们介绍了使用主成分分析法（PCA）计算各层变换的方法，从而将区块间的信号投射到其主成分上。最后，他们介绍了删除次要主成分如何对应于切掉网络的行或列。

Transformer网络的计算不变性

用 Q 表示正交矩阵：

注意，向量 x 乘以 Q 不会改变向量的 norm，因为在这项工作中，Q 的维度总是与 transformer D 的嵌入维度相匹配。

假设 X_ℓ 是 transformer 一个区块的输出，经过 RMSNorm 处理后，以 RMSNorm (X_ℓ) 的形式输入到下一个区块。如果在 RMSNorm 之前插入具有正交矩阵 Q 的线性层，并在 RMSNorm 之后插入 Q^⊤，那么网络将保持不变，因为信号矩阵的每一行都要乘以 Q、归一化并乘以 Q^⊤。此处有：

现在，由于网络中的每个注意力或 FFN 块都对输入和输出进行了线性运算，可以将额外的运算 Q 吸收到模块的线性层中。由于网络包含残差连接，还必须将 Q 应用于所有之前的层（一直到嵌入）和所有后续层（一直到 LM Head）的输出。

不变函数是指输入变换不会导致输出改变的函数。在本文的例子中，可以对 transformer 的权重应用任何正交变换 Q 而不改变结果，因此计算可以在任何变换状态下进行。作者将此称为计算不变性，并在下面的定理中加以定义。

定理 1：设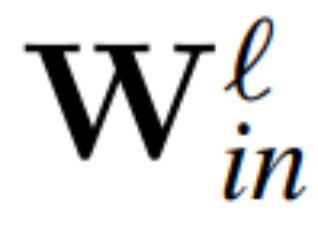和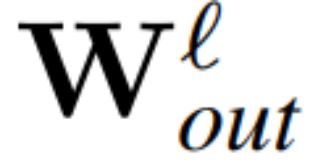为 RMSNorm 连接的 transformer 网络第 ℓ 块线性层的权重矩阵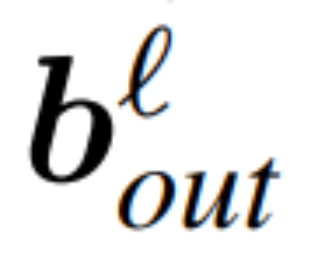，、为相应的偏置（如果有），W_embd 和 W_head 为嵌入矩阵和头矩阵。设 Q 是维数为 D 的正交矩阵，那么下面的网络就等同于原来的 transformer 网络：

复制输入偏置和头偏置：

可以通过算法 1 来证明，转换后的网络计算出的结果与原始网络相同。

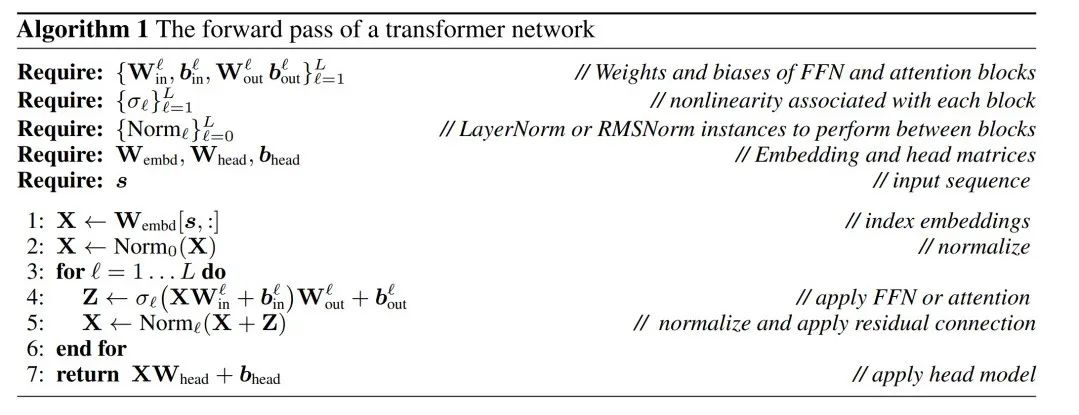
LayerNorm Transformer可以转换为RMSNorm

Transformer 网络的计算不变性仅适用于 RMSNorm 连接的网络。在处理使用 LayerNorm 的网络之前，作者先将 LayerNorm 的线性块吸收到相邻块中，从而将网络转换为 RMSNorm。

图 3 显示了 Transformer 网络（见图 2）的这种转换。在每个区块中，作者将输出矩阵 W_out 与均值减法矩阵 M 相乘，后者考虑了后续 LayerNorm 中的均值减法。输入矩阵 W_in 被前面 LayerNorm 块的比例预乘。嵌入矩阵 W_embd 必须进行均值减法，而 W_head 必须按照最后一个 LayerNorm 的比例重新缩放。这只是运算顺序的简单改变，不会影响网络输出。

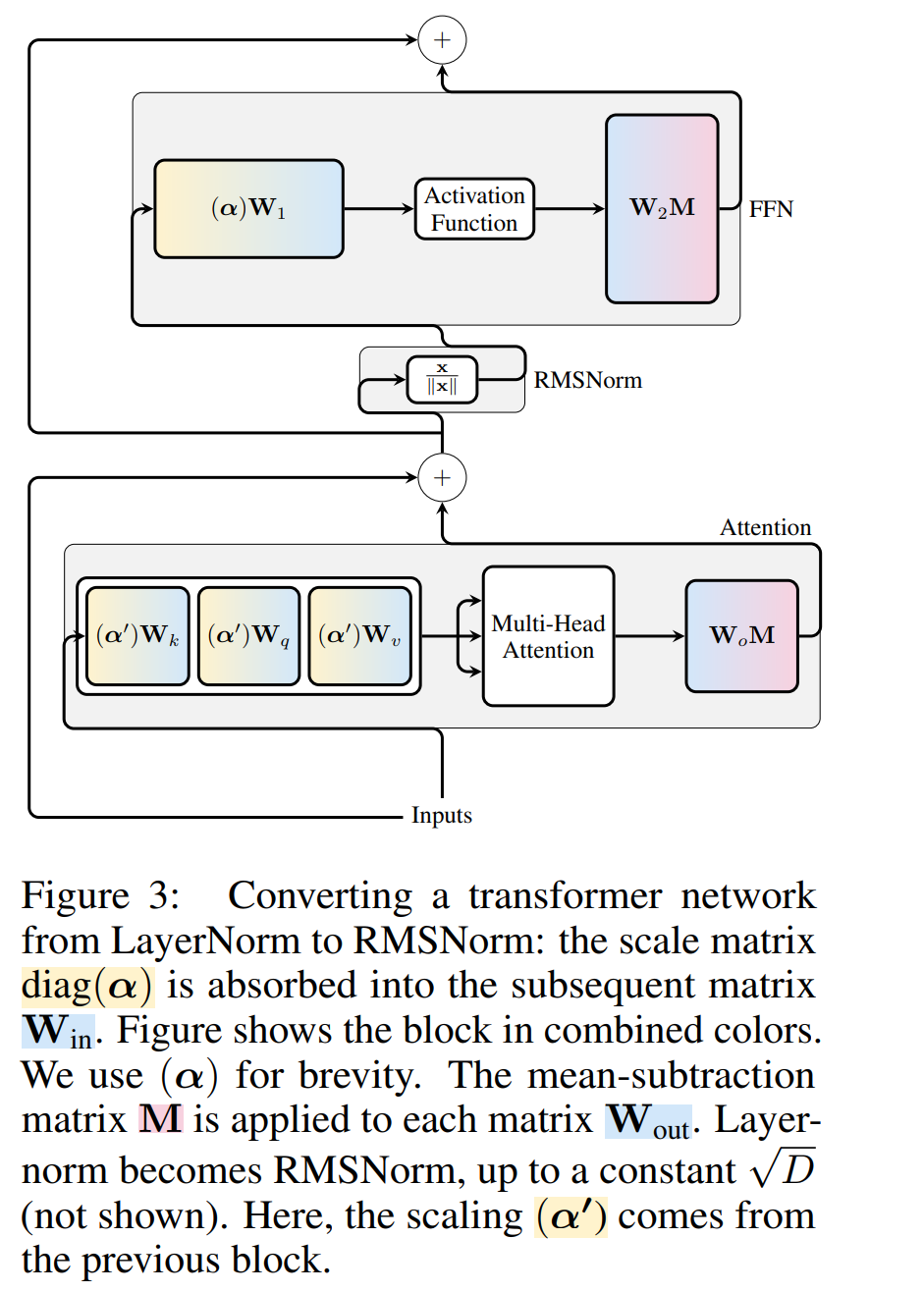
每个块的转换

现在 transformer 中的每个 LayerNorm 都已转换为 RMSNorm，可以选择任意 Q 来修改模型。作者最初的计划是从模型中收集信号，利用这些信号构建一个正交矩阵，然后删除部分网络。他们很快发现，网络中不同区块的信号并没有对齐，因此他们需要在每个区块应用不同的正交矩阵，即 Q_ℓ。

如果每个区块使用的正交矩阵不同，则模型不会改变，证明方法与定理 1 相同，但算法 1 第 5 行除外。在这里可以看到，残差连接和块的输出必须具有相同的旋转。为了解决这个问题，作者通过对残差进行线性变换来修改残差连接。

图 4 显示了如何通过对残差连接进行额外的线性运算，对不同的区块进行不同的旋转。与权重矩阵的修改不同，这些附加运算无法预先计算，并且会给模型增加少量（D × D）开销。尽管如此，还是需要通过这些操作来对模型进行切除操作，而且可以看到整体速度确实加快了。

为了计算矩阵 Q_ℓ，作者使用了 PCA。他们从训练集中选择一个校准数据集，在模型中运行（在将 LayerNorm 运算转换为 RMSNorm 之后），并提取该层的正交矩阵。更确切地说，如果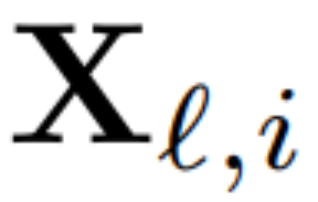他们使用转换后网络的输出来计算下一层的正交矩阵。更确切地说，如果是校准数据集中第 i 个序列的第 ℓ 个 RMSNorm 模块的输出，计算：

并将 Q_ℓ设为 C_ℓ 的特征向量，按特征值递减排序。

切除

主成分分析的目标通常是获取数据矩阵 X 并计算低维表示 Z 和近似重构：

其中 Q 是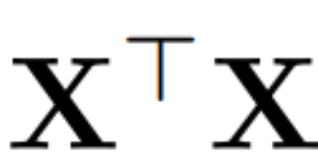的特征向量，D 是一个 D × D 小删除矩阵（包含 D × D 同位矩阵的 D 小列），用于删除矩阵左边的一些列。从 QD 是最小化的线性映射的意义上来说，重建是 L_2 最佳（L_2 optimal）的。

当对区块间的信号矩阵 X 应用 PCA 时，作者从未将 N × D 信号矩阵具体化，而是将删除矩阵 D 应用于构建该矩阵前后的运算。在上述运算中，该矩阵已乘以 Q。作者删除了 W_in 的行以及 W_out 和 W_embd 的列。他们还删除了插入到残差连接中的矩阵的行和列（见图 4）。

实验结果

生成任务

作者对经过 SliceGPT 和 SparseGPT 剪裁后大小不同的 OPT 和 LLAMA-2 模型系列在 WikiText-2 数据集中进行了性能评估。表 1 展示了模型经过不同级别的剪裁后保留的复杂度。相比 LLAMA-2 模型，SliceGPT 在应用于 OPT 模型时表现出了更优越的性能，这与作者根据模型频谱的分析得出的推测相符。

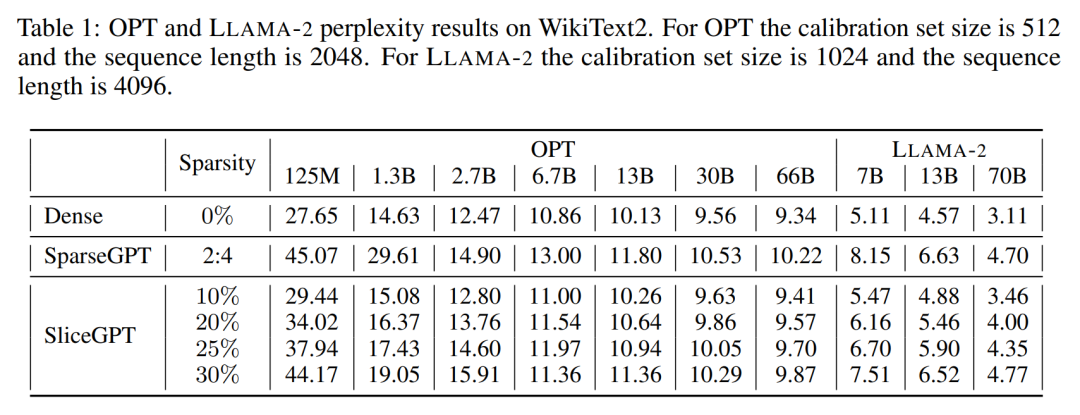
SliceGPT 的性能将随着模型规模的增大而提升。在对所有 LLAMA-2 系列模型剪裁 25% 情况下，SparseGPT 2:4 模式的表现都逊于 SliceGPT。对于 OPT，可以发现在除 2.7B 模型之外的所有模型中，30% 切除比例的模型的稀疏性都优于 2:4 的稀疏性。

零样本任务

作者采用了 PIQA、WinoGrande、HellaSwag、ARC-e 和 ARCc 五个任务来评估 SliceGPT 在零样本任务上的表现，他们在评估中使用了 LM Evaluation Harness 作为默认参数。

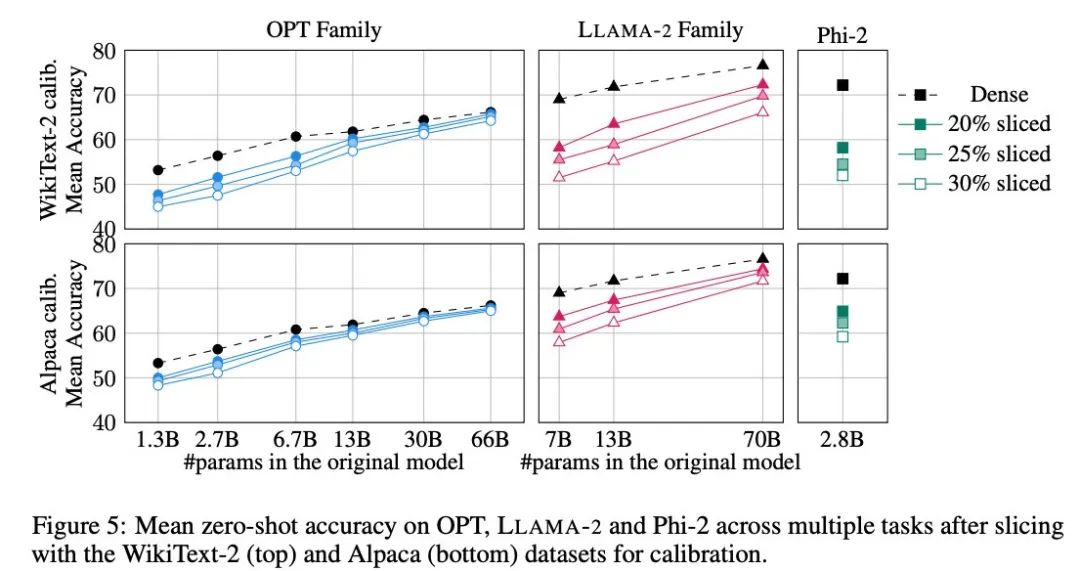
图 5 展示了经过剪裁的模型在以上任务中取得的平均分数。图中上行显示的是 SliceGPT 在 WikiText-2 中的平均准确率，下行显示的是 SliceGPT 在 Alpaca 的平均准确率。从结果中可以观察到与生成任务中类似的结论：OPT 模型比 LLAMA-2 模型更适应压缩，越大的模型经过剪裁后精度的下降越不明显。

作者在 Phi-2 这样的小模型中测试了 SliceGPT 的效果。经过剪裁的 Phi-2 模型与经过剪裁的 LLAMA-2 7B 模型表现相当。最大型的 OPT 和 LLAMA-2 模型可以被有效压缩，当从 66B 的 OPT 模型中删除 30% 时，SliceGPT 可以做到仅损失了几个百分点。

作者还进行了恢复微调（RFT）实验。使用 LoRA 对剪裁过的 LLAMA-2 和 Phi-2 模型进行了少量 RFT。

实验结果如图 6 所示。可以发现，RFT 的结果在 WikiText-2 和 Alpaca 数据集存在显著差异，模型在 Alpaca 数据集中展现了更好的性能。作者认为出现差异的原因在于 Alpaca 数据集中的任务和基准任务更接近。

对于规模最大的 LLAMA-2 70B 模型，剪裁 30% 再进行 RFT 后，最终在 Alpaca 数据集中的平均准确率为 74.3%，原稠密模型的准确率为 76.6%。经过剪裁的模型 LLAMA-2 70B 保留了约 51.6B 个参数，其吞吐量得到了显著提高。

作者还发现 Phi-2 无法在 WikiText-2 数据集中，从被剪裁过的模型中恢复原有准确率，但在 Alpaca 数据集中能恢复几个百分点的准确率。被剪裁过 25% 并经过 RFT 的 Phi-2 在 Alpaca 数据集中，平均准确率为 65.2%，原稠密模型的准确率为 72.2%。剪裁过的模型保留了 2.2B 个参数，保留了 2.8B 模型准确率的 90.3%。这表明即使是小型语言模型也可以有效剪枝。

基准吞吐量

和传统剪枝方法不同，SliceGPT 在矩阵 X 中引入了（结构化）稀疏性：整列 X 被切掉，降低了嵌入维度。这种方法既增强了 SliceGPT 压缩模型的计算复杂性（浮点运算次数），又提高了数据传输效率。

在 80GB 的 H100 GPU 上，将序列长度设置为 128，并将序列长度批量翻倍找到最大吞吐量，直到 GPU 内存耗尽或吞吐量下降。作者比较了剪裁过 25% 和 50% 的模型的吞吐量与原稠密模型 80GB 的 H100 GPU 上的吞吐量。剪裁过 25% 的模型最多实现了 1.55 倍的吞吐量提升。

在剪裁掉 50% 的情况下，最大的模型在使用一个 GPU 时，吞吐量实现了 3.13 倍和 1.87 倍的大幅增加。这表明在 GPU 数量固定的情况下，被剪裁过的模型的吞吐量将分别达到原稠密模型的 6.26 倍和 3.75 倍。

经过 50% 的剪裁后，虽然 SliceGPT 在 WikiText2 中的保留的复杂度比 SparseGPT 2:4 差，但吞吐量却远超 SparseGPT 的方法。对于大小为 13B 的模型，在内存较少的消费级 GPU 上，小模型的吞吐量可能也会有所提高。

推理时间

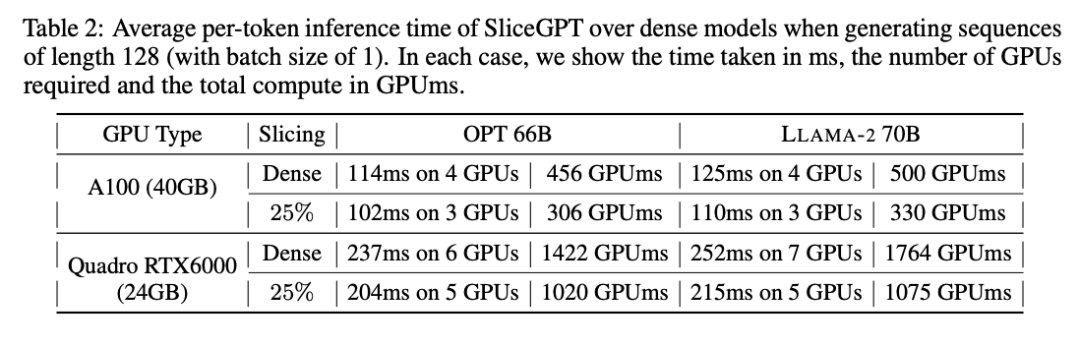
作者还研究了使用 SliceGPT 压缩的模型从端到端的运行时间。表 2 比较了在 Quadro RTX6000 和 A100 GPU 上，OPT 66B 和 LLAMA-2 70B 模型生成单个 token 所需的时间。

可以发现，在 RTX6000 GPU 上，对模型剪裁过 25% 后，推理速度提高了 16-17%；在 A100 GPU 上，速度提高了 11-13%。相比原稠密模型，对于 LLAMA-2 70B，使用 RTX6000 GPU 所需的计算量减少了 64%。作者将这种提升归功于 SliceGPT 采用了用较小的权重矩阵替换原权重矩阵，并使用了 dense kernels ，这是其他剪枝方案无法实现的。

作者表示，在撰写本文时，他们的基线 SparseGPT 2:4 无法实现端到端的性能提升。相反，他们通过比较 transformer 层中每个运算的相对时间，将 SliceGPT 与 SparseGPT 2:4 进行比较。他们发现，对于大型模型，SliceGPT (25%) 与 SparseGPT (2:4) 在速度提升和困惑度方面具有竞争力。

计算成本

所有 LLAMA-2、OPT 和 Phi-2 模型都可以在单个 GPU 上花费 1 到 3 小时的时间进行切分。如表 3 所示，通过恢复微调，可以在 1 到 5 个小时内压缩所有 LM。