特殊矩阵——三对角矩阵(Tridiagonal Matrix)

特殊矩阵——三对角矩阵(Tridiagonal Matrix)

注：压缩存储的矩阵可以分为特殊矩阵和稀疏矩阵。对于那些具有相同元素或零元素在矩阵中分布具有一定规律的矩阵，被称之为特殊矩阵。对于那些零元素数据远远多于非零元素数目，并且非零元素的分布没有规律的矩阵称之为稀疏矩阵。

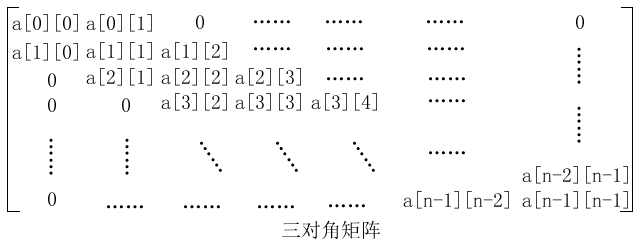
1. 三对角矩阵的概念

• 三对角矩阵就是对角线、邻近对角线的上下次对角线上有元素，其他位置均为0的矩阵。
• 三对角矩阵是一种特殊的上Hessenberg矩阵(这个就是上三角矩阵加上下三角部分的第一条次对角线有元素，其他都为0元素)。

2. 三对角矩阵的特性

• 设一个n*n的方阵A，对于矩阵A中的任一元素$a_{ij}$，当|i-j|>1时，有$a_{ij}=0(0≤i≤n-1，0≤j≤n-1)$时，矩阵A为三对角矩阵。
• 三对角矩阵中除主对角线及在主对角线上下最邻近的两条对角线上的元素外，所有其他元素均为0。

3. 三对角矩阵的压缩存储

• 可以利用三对角矩阵的上述特性，只存储主对角线及其上、下两侧次对角线上的元素，其他的零元素一律不存储。对一个n*n的三对角方阵A，元素总数有$n^2$个，而其中非零的元素共有3*n-2个。因此，存储三对角矩阵时最多只需存储3*n-2个元素。
  
• 可以仿照对称矩阵的压缩存储，可用一维数组B存储三对角矩阵A(这要区分两种存储方式：行优先方式和列优先方式)。
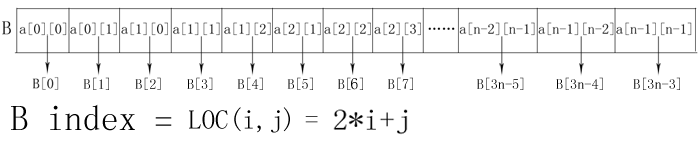
  (1)行优先方式存储
  
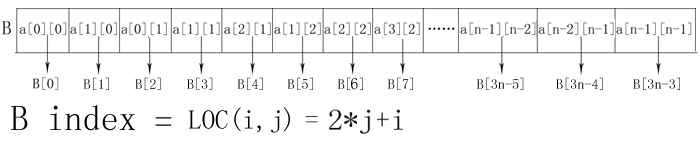
  (2)列优先方式存储
  

4. 三对角矩阵的实现

• 文件：TridiagonalMatrix.h

  
  #include <iostream>
  
  
  using namespace std;
  
  //压缩存储后，存储对称方阵时最多只需存储n*(n+1)/2个元素
  
  #define GetTotalLen(n) 3 * n - 2                
  
  
  //按行优先方式存放三对角矩阵，矩阵元素下标对应的一维数组的下标
  
  #define GetIndexRow(i, j) 2 * i + j 
  
  
  //按列优先方式存放三对角矩阵，矩阵元素下标对应的一维数组的下标
  
  #define GetIndexCol(i, j) 2 * j + i
  
  
  
  class TridiagonalMatrix
  {
  public:
      TridiagonalMatrix(int order);
  
      ~TridiagonalMatrix();
  
  public:
      void create();                      //创建矩阵
  
      void destroy();                     //销毁矩阵
  
      void transpos();                    //矩阵转置
  
      int get_order();                    //获取矩阵阶数
  
      int* compressed_storage_row();      //压缩存储特殊矩阵——三对角矩阵，按行优先方式存放
  
      int* compressed_storage_col();      //压缩存储特殊矩阵——三对角矩阵，按列优先方式存放
  
      bool is_tridiagonal();              //判断矩阵是否为三对角矩阵
  
  public:
      friend ostream& operator<<(ostream& os, TridiagonalMatrix& m);    //输出矩阵
  
  private:
      int _order;
      int **_matrix;
  };

• 文件：TridiagonalMatrix.cpp

  
  #include "TridiagonalMatrix.h"
  
  
  #include <math.h>
  
  
  TridiagonalMatrix::TridiagonalMatrix(int order)
  : _order(order), _matrix(new int*[order])
  {
      create();
  }
  
  TridiagonalMatrix::~TridiagonalMatrix()
  {
      destroy();
  }
  
  void TridiagonalMatrix::create()
  {
      for (int i = 0; i < _order; i++)
      {
          _matrix[i] = new int[_order];
          for (int j = 0; j < _order; j++)
          {
              if (abs(i-j) > 1)
              {
                  _matrix[i][j] = 0;
              }
              else
              {
                  _matrix[i][j] = 1;
              }
          }
      }
  }
  
  void TridiagonalMatrix::destroy()
  {
      for (int i = 0; i < _order; i++)
      {
          delete[] _matrix[i];
      }
      delete[] _matrix;
      _matrix = NULL;
  }
  
  void TridiagonalMatrix::transpos()
  {
      int temp = 0;
      for (int i = 0; i < _order; i++)
      {
          for (int j = 0; j < _order; j++)
          {
              temp = _matrix[i][j];
              _matrix[i][j] = _matrix[j][i];
              _matrix[j][i] = temp;
          }
      }
  }
  
  
  int TridiagonalMatrix::get_order()
  {
      return _order;
  }
  
  int* TridiagonalMatrix::compressed_storage_row()
  {
      int index = 0;
      int total_count = GetTotalLen(_order);
      int *a = new int[total_count];
      for (int i = 0; i < _order; i++)
      {
          for (int j = 0; j < _order; j++)
          {
              if (abs(i-j) <= 1)
              {
                  index = GetIndexRow(i, j);
                  a[index] = _matrix[i][j];
              }
          }   
      }
      return a;
  }
  
  int* TridiagonalMatrix::compressed_storage_col()
  {
      int index = 0;
      int total_count = GetTotalLen(_order);
      int *a = new int[total_count];
      for (int j = 0; j < _order; j++)
      {
          for (int i = 0; i < _order; i++)
          {
              if (abs(i - j) <= 1)
              {
                  index = GetIndexCol(i, j);
                  a[index] = _matrix[i][j];
              }
          }
      }
      return a;
  }
  
  bool TridiagonalMatrix::is_tridiagonal()
  {
      for (int i = 0; i < _order; i++)
      {
          for (int j = 0; j < _order; j++)
          {
              if ((abs(i-j) > 1) && (_matrix[i][j] != 0))
              {
                  return false;
              }
          }
      }
      return true;
  }
  
  ostream& operator<<(ostream& os, TridiagonalMatrix& m)
  {
      os << "三对角矩阵：" << endl;
      for (int i = 0; i < m._order; i++)
      {
          for (int j = 0; j < m._order; j++)
          {
              os << m._matrix[i][j] << " ";
          }
          os << endl;
      }
      return os;
  }

• 文件：main.cpp

  
  #include "TridiagonalMatrix.h"
  
  
  int main()
  {
      int n = 0;
      cout << "请输入三对角矩阵的阶数，n = ";
      cin >> n;
  
      TridiagonalMatrix matrix(n);
      if (true == matrix.is_tridiagonal())
      {
          cout << "$ 输出三对角矩阵：" << endl;
          cout << matrix;//或operator<<(cout, matrix);
      }
  
      matrix.transpos();
      if (true == matrix.is_tridiagonal())
      {
          cout << "$ 输出转置后的三对角矩阵：" << endl;
          cout << matrix;//或operator<<(cout, matrix);
      }
  
      cout << "\n$ 输出压缩存储后的一维数组(按行优先方式存放)：" << endl;
      int *arrayr = matrix.compressed_storage_row();
      for (int i = 0; i < GetTotalLen(matrix.get_order()); i++)
      {
          cout << arrayr[i] << " ";
      }
      cout << endl;
      delete[] arrayr;
  
      cout << "\n$ 输出压缩存储后的一维数组(按列优先方式存放)：" << endl;
      int *arrayc = matrix.compressed_storage_col();
      for (int i = 0; i < GetTotalLen(matrix.get_order()); i++)
      {
          cout << arrayc[i] << " ";
      }
      cout << endl;
      delete[] arrayc;
  
      system("pause");
      return 0;
  }

---

参考文献：
[1]《数据结构(用面向对象方法与C++语言描述)(第2版)》殷人昆——第四章
[2] 百度搜索关键字：三对角线矩阵、多对角线矩阵