（二）大数据处理：基于MapReduce的大图划分算法综述

【声明：鄙人菜鸟一枚，写的都是初级博客，如遇大神路过鄙地，请多赐教；内容有误，请批评指教，如有雷同，属我偷懒转运的，能给你带来收获就是我的博客价值所在。】
   今天一位同事跟我谈起Hadoop，刚好这期博客我也正准备写点这方面相关的综述，就跟他聊了聊。谈起Hadoop不得不谈及MapReduce，它是基于Hadoop分布式大数据处理平台的一个非常重要的计算框架，通俗些讲：MapReduce就像是一种套路，按着这种套路来解决普通计算模式难以接受的量级数据运算，分步分解、各个击破。我不知道这样说算不算通俗精准，但就是这个意思。这里我也不打算就Hadoop和MapReduce做全面且详细的概述，毕竟不是一两句话就能讲清楚的，所以默认观众姥爷们有这些基础知识，没有的话也没关系，这次谈的是基于MapReduce的大图划分的一些常用算法，讲的很基础，中间会有一段专门解释MapReduce。下面移步正文（可能在格式上有些正式了，希望别反感）：

1 背景及意义

  在今天这个信息化社会中，随着互联网用户的急剧增加，越来越多的网络数据问题摆在了我们面前。而在大数据时代下，大规模图数据处理问题便是一大热点。类似于网状图，如果将每个网络用户看作图中的节点，而将用户与用户之间的关系看作图中的边，那么整个网络就可看作一张网络图，大量的网络图组成的集合便是图数据。随着网络用户规模的不断扩大，与之对应的网络图结构愈加复杂，甚至有数十亿个节点和上万亿条边，普通的单台计算机由于运算内存的限制，无法承载这种巨大的处理任务，这给数据处理中常见的图计算（如获取连通分量和PageRank）带来了巨大的挑战。
  解决单机能力的局限性问题，最好的方法就是利用分布式计算，即将大规模图数据划分成多个子图装载到分区中，利用大型的分布式系统进行处理。为了提高不同分区间的并行处理速度，需要保持这些子图的规模均衡，同时减少通信开销，所以连接不同分区的边数应当足够小。所以，基于MapReduce的大规模图数据划分算法研究对解决图论计算问题具有极大的意义。
  本文将综合前人的研究，介绍图划分算法的研究现状，分析、比较它们的性能特点，以及详细阐述基于MapReduce的分布式图划分算法，从而使读者能系统而全面地了解图划分与分布式图划分算法。

2 图数据划分的研究现状

  图数据划分问题是经典的NP（Non-deterministic Polynomial）完全问题，通常很难在有限的时间内找到图划分的最优解[1]。尽管其是难解问题，从20 世纪90 年代初期至今，国内外研究者不断对图划分及其相关问题进行深入研究，提出了许多性能较好的图划分算法。现主要有谱方法、几何方法、启发式方法、智能优化算法、多层划分算法等。[2]

2.1 谱方法

  1990 年，R. Leland 和B. Hendrickson 提出了谱方法。谱方法主要是针对图的二划分而言的。它的基本思想是用图矩阵的第二大特征值和特征向量来实现图的划分。谱方法能为许多不同类的问题提供较好的划分，但是谱方法的计算量非常大。H. Simon 和S. Barnard 于1993 年对谱方法进行了改进，具体是用多层的谱二分(MSB) 有效地减少了算法求解特征向量的执行时间。

2.2 几何方法

  几何方法根据给定图的几何信息来寻找较好的划分。几何方法主要包括坐标嵌套二分法、递归惯性二分法、空间填充曲线方法。1987 年，S. Bokari 和M. Berger 提出了坐标嵌套二分法。其思想是：先选择网格在平面坐标上具有最长长度的一维，接着沿着选中那一维的方向对网格进行划分。该方法是一种递归二分法，其算法有很快的执行速度，但其缺点是划分质量非常低，而且还会产生不连通的子区域。为解决上述缺点，M. Heath 和P. Raghavan 于1995 年对其进行了改进，然而只能沿着两坐标轴垂直或者平行方向划分。递归惯性二分法是在坐标嵌套二分法的基础上提出来的，其不再用平面坐标轴，而是用惯性主轴，从而降低了不连通子区域的数量；但是递归惯性二分法在划分时还是仅能按照坐标轴的某一维进行。1994 年，S. Ranka 和C. Ou 提出了空间填充曲线方法，该方法是一种基于多维的划分方法。其首先对多维曲线上的数据单元进行排序，这主要是依据网格的质心来实现排序。然后根据排序的结果进行图的划分。

2.3 启发式方法

  W. Kernighan 和S. Lin 提出了KL 算法，它是一种比较典型的基于启发式规则的求解策略。它的主要思想是先将图随机化成两等分，然后对交换任意两个顶点能导致的收益值进行估价，再高效地从中选择收益最高的点进行交换。该算法通常处理一万个顶点以内的图。 M. Fiduccia 和M. Mattheyses 提出的FM 算法对KL 算法进行了改进。FM 算法采用单点移动，并引入了桶列表数据结构，减少了时间复杂度。该类方法不需要知道节点的坐标信息，而是需要根据节点之间的连接信息进行划分。2000 年，S. Dutt 和W. Deng 从顶点的移动次数对FM 算法进行改进。2002 年，S. Dutt 和W. Deng 又从收益的计算方式进行改进。

2.4 智能优化算法

  因智能优化算法模拟自然界已知的进化方法而具有一定的优越性，一直备受来自各个领域研究者的关注。近年来智能优化算法被广泛用来解决图划分问题。2007年，P. Chardaire 等人[3]提出了一种基于种群的元启发式算法PROBE (population reinforced optimization based exploration)。PROBE 算法有些类似于遗传算法，但该算法没有选择、突变和置换的概念，因而比遗传算法方法要简单。

2.5 多层划分算法

  为了处理规模较大的图，文献[4]提出了多层的图划分框架METIS。多层划分算法包括3 个阶段：粗糙化 (coarsening) 阶段、初始划分、反粗糙化阶段(uncoarsening)。第一阶段通过粗糙化 (coarsening) 技术将大图约化为可接受的小图；第二阶段将第一阶段获得的小图进行随机划分，并进行优化；第三阶段通过反粗糙化 (uncoarsening) 技术以及优化技术将小图的划分还原为原图的划分。该算法广泛地应用在各类大图的划分，对于百万规模以内的图，通常具有较好的实际效果。

2.6 小结

  图划分问题普遍存在较高的计算复杂度，但图数据在现实中具有重要的价值，这也是人们不断追求更简易的图划分算法的原因。上文提到的五种图划分算法在处理方法与结构上各具特色，也各有优劣，但就所能处理的图数据规模上来讲，分成集中式图划分算法与分布式图划分算法。
集中式图划分算法 可以处理节点数和边数较少的图，包括局部改进图划分算法和全局图划分算法，其中局部改进图划分算法中比较经典的是KL算法[5]和FM算法[6]，全局图划分算法中比较经典的是Laplace图特征值谱二分法[7]和多层图划分算法[8]。这些算法具有较高的时问复杂度，无法处理节点数为百万级以上的图，因此这些算法不适用于大数据时代中大规模的图处理。
分布式图划分算法  是针对近些年出现的大规模网络图而研究出来的，分为静态图划分算法和动态图划分算法，其中静态图划分算法的工作比较多，主要包括BHP算法[9]、静态Mizan算法[10]、BLP算法[11]等；动态图划算法经典的主要包括动态Mizan算法[12]和xDGP算法[13]等。
  相比集中式图划分算法，分布式的图算法在大数据时代具有无法比拟的优势，所以本文接下来详细介绍基于MapReduce的分布式图划分算法。

3 基于MapReduce的分布式图划分算法

3.1 MapReduce模型

  MapReduce 是一种编程模型，用于大规模数据集（大于1TB）的并行运算。在大规模数据集的处理与计算方面有着极大的优势，且作为开源应用平台，MapReduce已被广泛应用于Hadoop、Phoenix、Mars、Cell MapReduce、FPMR、Ussop。[14] MapReduce 适合具有大量相同的基本计算的信息处理场合（例如，web 图中的节点），MapReduce 思想来源于高阶函数式编程，提供了一个抽象定义的Mapper（映射函数，指定每个record的计算）和Reducer（归约函数，指定map输出结果的整合），Mapper把一组键值对映射成一组新的键值对（作为处理基元），指定并发的Reducer对生成的键值对进行并行操作。这两个阶段的处理结构如图 1 所示。
  根据 MapReduce 编程模型，开发人员只需提供对应的Mapper和Reducer实现代码。在分布式文件系统（DFS）上，执行状态（runtime）负责创建分布式集群上程序运行的环境。除此外，它可以实现调度（数据移动代码）、处理故障和大型分布式排序和洗牌操作之间的映射问题。
作为一种优化，MapReduce 支持combiner（组合器）的使用，与Reducer机制类似，只是他们可以直接作用于Mapper的输出，故而可以将它看作mini-Reducer。Combiner运行在集群中每个节点之间，但不能使用其他节点的分立结果。鉴于中间键值对最终必须通过网络Shuffle与Sort匹配到合适的Reducer，combiner允许程序员归约部分结果，从而减少了网络流量。

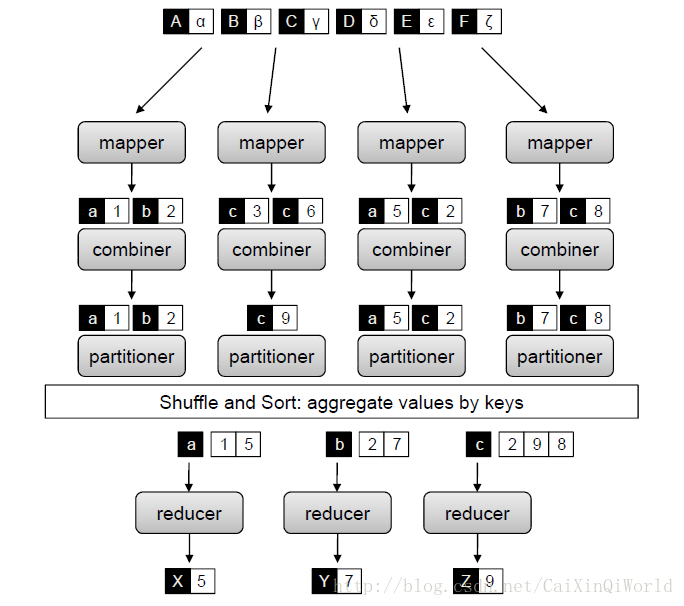
        图 1︰ MapReduce模型的map与reduce阶段的处理结构示意图。

  MapReduce的一个重要部分便是partitioner（划分），它负责划分中间键域和为Reducer分配中间键值对。默认的partitioner会计算Reducer数目模数的哈希值。Partitioner在合适的哈希函数的帮助下可大致将中间键域划分均匀，但这不能保证良好的负载平衡，因为可能出现高度偏态分布也具有相同的关联键值。

3.2 MapReduce图划分算法

  定义一个标准的矢量图 $G = (V, E)$，其中组成的节点 $V$和矢量边 $E$，且 $N^+ (v_i )={v_j│(v_i,v_j )∈E}$ 和 $N^- (v_i )={v_j│(v_j,v_i )∈E}$ 是所有相邻节点vi组成的集合，图划分就是给定合适的矢量图G，将节点集V划分为互不相交的k个子集 $V_1, V_2, …, V_k$。标量图还默认支持用两个交互矢量边替换每个标量边，节点和边上可能附加有额外的元数据。举个简单的例子，社会网络（其中节点代表人）可能有附加到边和节点上的属性信息（如指示属性的朋友或配偶关系）及统计信息（如年龄、性别、住址）。图划分方法需要满足两个主要原则：一是子图与子图之间相连的边尽量少，即交互边数小；二是子图与子图的规模应当差不多，即负载均衡。
  基于以上的图划分定义及划分算法满足的原则，这里介绍一大类作用在稀疏矢量图上的迭代图算法，其中每次迭代过程如下︰
1. 计算每个节点（作为函数）的内部状态和局部图结构；
2. 将各部分结果（以任意消息形式存在）通过矢量边传递给每个节点的相邻节点；
3. 基于传入的部分结果，计算每个节点并同时改变节点的内部状态。
  通常情况下，这种算法需迭代一定次数，且每一次迭代过程均要使用迭代图上一次的历史状态作为下 一次迭代的输入，直到满足迭代终止条件。运用以上图算法的一个经典例子就是 PageRank，它是基于拓扑结构的知名算法，用来计算节点（Page ID）在图中的重要性。对于图中每个节点，PageRank 计算 P(vi) （即：图中节点vi的概率），一个节点的概率主要取决于图的拓扑结构，但计算上还会考虑阻尼因子d。
  PageRank 最初被用于网页（具有超链接结构）的Rank（排序处理），但利用图中的拓扑结构关系，PageRank也可应用于节点的Rank。而且它也为很多重要的图分析算法奠定了基础[15]。

4 结语

  对于大数据时代下各种复杂的大规模图数据处理问题，研究图划分算法（尤其是基于MapReduce的分布式图划分算法）已展现出巨大的优势与价值，也具有重大的现实意义，但同时也面临着众多的问题与挑战。借助分布式计算技术及新兴的高速算法，未来对大规模图划分问题的研究必将有重大突破与发展。

参考文献

[1] Benlic U, Hao J K. Hybrid Metaheuristics for the Graph Partitioning Problem[M]// Hybrid Metaheuristics. 2013:157-185.
[2] 郑丽丽. 图划分算法综述[J]. 科技信息, 2014(4):145-145.
[3] Lipponen,L. Exploring foundations for computer-supported collaborative learning[A]. In Gerry Stahl (Ed.). Computer Support Collaborative Learning: Foundations for a CSCL Community. Proceedings of CSCL 2002.HillsdaIe, New Jersey: Lawrence Erlbaum Associatesjnc.,2002:72-81.
[4] 项国雄, 张小辉. 学习支持服务思想溯源[J]. 中国远程教育,2005,9.
[5] Dutt S. New faster Kernighan-Lin-type graph-partitioning algorithms[C]// Ieee/acm International Conference on Computer-Aided Design, 1993. Iccad-93. Digest of Technical Papers. 1993:370-377.
[6] Fiduccia C M, Mattheyses R M. A linear-time heuristic for improving network partitions[M]. 1988.
[7] Pothen A, Simon H D, Liou K P. Partitioning sparse matrices with eigenvectors of graphs[J]. Siam Journal on Matrix Analysis & Applications, 1990, 11(3):430-452.
[8] Karypis G, Kumar V. A Fast and High Quality Multilevel Scheme for Partitioning Irregular Graphs[J]. Siam Journal on Scientific Computing, 2006, 20(1):359–392.
[9] 周爽, 鲍玉斌, 王志刚等. BHP:面向BSP模型的负载均衡Hash图数据划分, 2013年7月23日[J]. 计算机科学与探索, 2013.
[10] Khayyat Z, Awara K, Jamjoom H, et al. Mizan: Optimizing Graph Mining in Large Parallel Systems[J]. King Abdullah University of Science & Technology, 2012.
[11] Ugander J, Backstrom L. Balanced label propagation for partitioning massive graphs[C]// ACM International Conference on Web Search and Data Mining. 2013:507-516.
[12] Khayyat Z, Awara K, Alonazi A, et al. Mizan: a system for dynamic load balancing in large-scale graph processing[C]// ACM European Conference on Computer Systems. ACM, 2013:169-182.
[13] Vaquero L, Cuadrado F, Logothetis D, et al. xDGP: A Dynamic Graph Processing System with Adaptive Partitioning[J]. Eprint Arxiv, 2013.
[14] Li Jian-Jiang, Jian Cui, Wang Dan, Yan Lin, Huang Yi-Shuang, “Survey of MapReduce Parallel Programming Model”, ACTA ELECTRONICA SINICA, Vol.39, No.11, (2011), pp.2635-2642.
[15] Kleinberg J M. Authoritative Sources in a Hyperlinked Environment[C]// 1999:604–632.