最优查找树

     以下内容主要参考了严蔚敏版的数据结构教材。
     对于一个已经有序的序列 { k 0 , k 1 , k 2 , . . . , k n − 1 } \{k_0,k_1,k_2,...,k_{n-1}\} {k0​,k1​,k2​,...,kn−1​}，各关键字对应的权值分别为 { w 0 , w 1 , w 2 , . . . , w n − 1 } \{w_0,w_1,w_2,...,w_{n-1}\} {w0​,w1​,w2​,...,wn−1​}，需要构建一颗二叉树使得其带权路径长度$\sum _{i=0}^{n-1}{w}_i\times h_i$最小，其中$h_i$为关键字$k_i$对应的节点在二叉树中所在的层数。该二叉树称为最优查找树。图1给出了一个最优查找树的例子。下面直接上代码（源码来自于这里），图2给出了递归构建最优查找树的递归调用过程。

　 图1.

　 图2.

class BinaryNode
{
public:
	BinaryNode(int value=0,BinaryNode*left = nullptr, BinaryNode* right=nullptr)
	{
		key=value;
		leftChild=left;
		rightChild=right;
	}
	int getKey()
	{
		return key;
	}
	BinaryNode* getLeft()
	{
		return leftChild;
	}
	BinaryNode* getRight()
	{
		return rightChild;
	}
private:
	int key;
	BinaryNode* leftChild;
	BinaryNode* rightChild;
};

void traverseBinaryTree(BinaryNode* root)
{
	if (root!=nullptr)
	{
		cout << "Node key is:" << root->getKey() << endl;
		traverseBinaryTree(root->getLeft());
		traverseBinaryTree(root->getRight());
	}
	else
	{
		cout << "root is nullptr!!!!" << endl;
		return;
	}
	return;
}

// A utility function to get sum of  
// array elements freq[i] to freq[j]  
int sum(int freq[], int i, int j);

// A recursive function to calculate  
// cost of optimal binary search tree  
int optCost(BinaryNode * &root, int keys[],int freq[], int i, int j)
{
	BinaryNode* leftSubTree = nullptr;
	BinaryNode* rightSubTree = nullptr;
	// Base cases  
	if (j < i)  // no elements in this subarray  
	{
		return 0;
	}

	if (j == i) // one element in this subarray  
	{
		root = new BinaryNode(keys[i], leftSubTree, rightSubTree);
		return freq[i];
	}
	BinaryNode* leftTempSubTree = nullptr;
	BinaryNode* rightTempSubTree = nullptr;
	int cost = 0;
	int leftCost = 0;
	int rightCost = 0;
	int minIndex = 0;

	// Get sum of freq[i], freq[i+1], ... freq[j]  
	int fsum = sum(freq, i, j);

	// Initialize minimum value  
	int min = INT_MAX;

	// One by one consider all elements  
	// as root and recursively find cost  
	// of the BST, compare the cost with 
	// min and update min if needed  
	for (int r = i; r <= j; ++r)
	{
		BinaryNode* leftTempSubTree = nullptr;
		BinaryNode* rightTempSubTree = nullptr;
		leftCost = optCost(leftTempSubTree, keys,freq, i, r - 1);
		rightCost=optCost(rightTempSubTree, keys,freq, r + 1, j);
		cost = leftCost + rightCost;
		if (cost < min)
		{
			minIndex = r;
			min = cost;
			leftSubTree = leftTempSubTree;
			rightSubTree = rightTempSubTree;
		}
	}
	root = new BinaryNode(keys[minIndex], leftSubTree, rightSubTree);
	// Return minimum value  
	return min + fsum;
}

// The main function that calculates  
// minimum cost of a Binary Search Tree.  
// It mainly uses optCost() to find  
// the optimal cost.  
int optimalSearchTree(BinaryNode * &root, int keys[],
	int freq[], int n)
{
	// Here array keys[] is assumed to be  
	// sorted in increasing order. If keys[]  
	// is not sorted, then add code to sort  
	// keys, and rearrange freq[] accordingly.  
	return optCost(root, keys,freq, 0, n - 1);
}

// A utility function to get sum of  
// array elements freq[i] to freq[j]  
int sum(int freq[], int i, int j)
{
	int s = 0;
	for (int k = i; k <= j; k++)
		s += freq[k];
	return s;
}

//测试程序
int main()
{
	int keys[] = { 10, 12, 20 };
	int freq[] = { 34, 8, 50 };
	int n = sizeof(keys) / sizeof(keys[0]);
	BinaryNode* root = nullptr;
	cout << "Cost of Optimal BST is "
		<< optimalSearchTree(root,keys, freq, n)<<endl;
	traverseBinaryTree(root);
	return 0;
}

     从以上源码和图示可以看出以上算法的时间复杂度接近于指数级，且有些范围的数据被重复调用，因此效率很差。因此在严蔚敏的数据结构教材中引进了一种近似最优查找树的算法（次优查找树），其性能与最优查找树接近但是复杂度却大大降低。现在叙述如下。
     对于一个已经有序的序列 { k l , k l + 1 , k l + 2 , . . . , k h } \{k_l,k_{l+1},k_{l+2},...,k_{h}\} {kl​,kl+1​,kl+2​,...,kh​}，各关键字对应的权值分别为 { w l , w l + 1 , w l + 2 , . . . , w h } \{w_l,w_{l+1},w_{l+2},...,w_h\} {wl​,wl+1​,wl+2​,...,wh​}。现在取第i$(l<=i<=h)$个记录作为构建的次优二叉查找树的根节点，使得$\Delta P=|{\sum }_{j=i+1}^h{w}_j-{\sum }_{j=l}^{i-1}{w}_j|$最小，然后分别对子序列 { k l , k l + 1 , k l + 2 , . . . , k i − 1 } \{k_l,k_{l+1},k_{l+2},...,k_{i-1}\} {kl​,kl+1​,kl+2​,...,ki−1​}和 { k i + 1 , k i + 2 , k i + 3 , . . . , k h } \{k_{i+1},k_{i+2},k_{i+3},...,k_{h}\} {ki+1​,ki+2​,ki+3​,...,kh​}构造两颗次优查找树并作为根节点的左右子树，递归以上操作就可以得到一颗次优查找树。
     为了便于计算$\Delta P$,引入累计权值和$s{w}_i={\sum }_{j=l}^i{w}_j$并假设$w_{l-1}=0$且$s{w}_{l-1}=0$（其实$w$和$sw$的索引范围是$[l,h]$，加入这额外的两项是为了以下定义的完整性）则有：
$$\{\begin{array}{r}s{w}_{i-1}-s{w}_{l-1}=\sum _{j=l}^i{w}_j\\ s{w}_h-s{w}_i=\sum _{j=i+1}^h{w}_j\end{array}$$
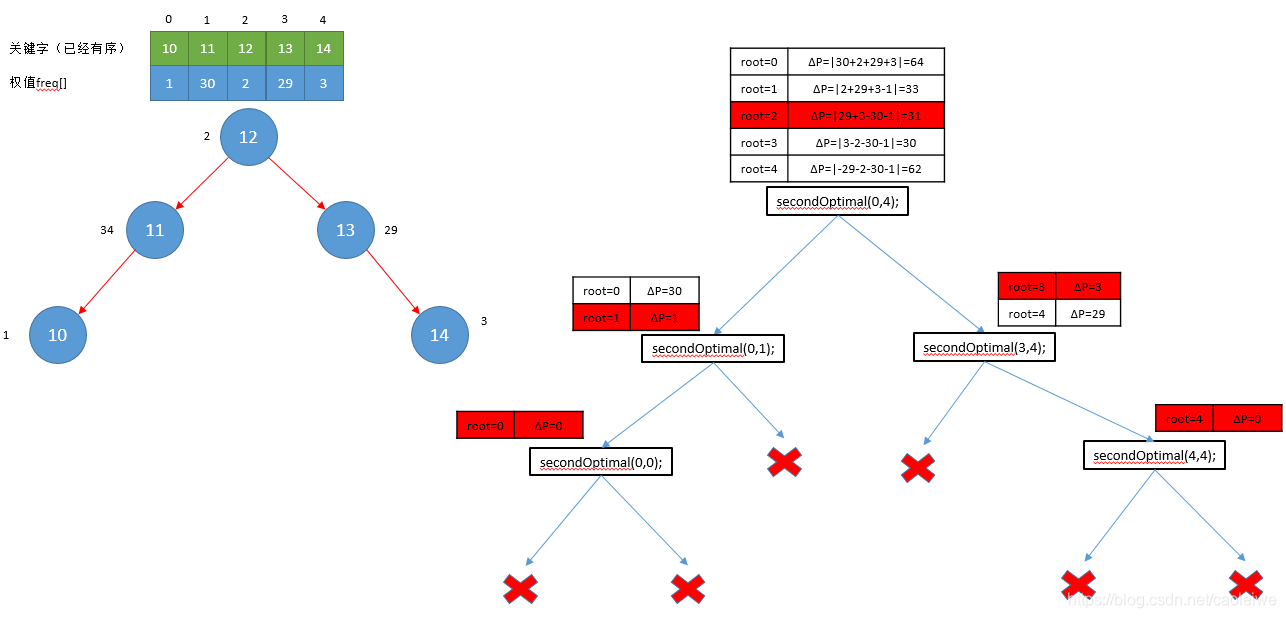
因此$\Delta P=|(s{w}_h-s{w}_i)-(s{w}_{i-1}-s{w}_{l-1})|=|(s{w}_h+s{w}_{l-1})-s{w}_i-s{w}_{i-1})|$，即可得如下的源码。一个简单的例子如图3所示。

class BinaryNode
{
public:
	BinaryNode(int value = 0, BinaryNode* left = nullptr, BinaryNode* right = nullptr)
	{
		key = value;
		leftChild = left;
		rightChild = right;
	}
	int getKey()
	{
		return key;
	}
	BinaryNode* getLeft()
	{
		return leftChild;
	}
	BinaryNode* getRight()
	{
		return rightChild;
	}
private:
	int key;
	BinaryNode* leftChild;
	BinaryNode* rightChild;
};

void traverseBinaryTree(BinaryNode* root)
{
	if (root != nullptr)
	{
		cout << "Node key is:" << root->getKey() << endl;
		traverseBinaryTree(root->getLeft());
		traverseBinaryTree(root->getRight());
	}
	else
	{
		cout << "root is nullptr!!!!" << endl;
		return;
	}
	return;
}

// A utility function to get sum of  
// array elements freq[i] to freq[j] 
int sum(int freq[], int i, int j)
{
	int s = 0;
	for (int k = i; k <= j; k++)
		s += freq[k];
	return s;
}


void secondOptimal(BinaryNode* &root,int keys[], int sw[],int low,int high)
{
	BinaryNode* leftTempSubTree = nullptr;
	BinaryNode* rightTempSubTree = nullptr;
	int i = low;
	int min = abs(sw[high]-sw[low]);
	int dw = 0;
	if (low == 0)
	{
		dw = sw[high];
	}
	else
	{
		dw = sw[high] + sw[low - 1];
	}

	for (int j=low+1;j<=high;j++)
	{
		if(abs(dw - sw[j] - sw[j - 1])<min)
		{
			i = j;
			min = abs(dw - sw[j] - sw[j - 1]);
		}

	}
	if (i==low)
	{
		leftTempSubTree = nullptr;
	}
	else
	{
		secondOptimal(leftTempSubTree, keys, sw, low, i-1);
	}
	if (i == high)
	{
		rightTempSubTree= nullptr;
	}
	else
	{
		secondOptimal(rightTempSubTree, keys, sw, i+1, high);
	}

	root = new BinaryNode(keys[i], leftTempSubTree, rightTempSubTree);
}

void createSOSTree(BinaryNode*& root,int keys[], int fre[],int n )
{
	if (n==0)
	{
		root = nullptr;
	}
	else
	{
		int* sw = new int[n];
		for (int i=0;i<n;i++)
		{
			sw[i] = sum(fre,0, i);
		}
		for (int j = 0; j < n; j++)
		{
			cout<<"sw[i]="<<sw[j] <<endl;
		}
		
		secondOptimal(root, keys, sw, 0, n-1);
	}
}

//测试程序
int main()
{
	int keys[] = { 10, 11,12, 13,14 };
	int freq[] = { 1,30,2, 29, 3 };
	int n = sizeof(keys) / sizeof(keys[0]);
	BinaryNode* root = nullptr;
    createSOSTree(root,keys, freq, n);
	traverseBinaryTree(root);
	return 0;
}

　 图3.

     解决以上构建最优二叉查找树的算法中遇见的问题的另一种解决办法是动态规划。对于一个已经有序的序列 { k 0 , k 1 , k 2 , . . . , k n − 1 } \{k_0,k_1,k_2,...,k_{n-1}\} {k0​,k1​,k2​,...,kn−1​}，各关键字对应的权值分别为 { w 0 , w 1 , w 2 , . . . , w n − 1 } \{w_0,w_1,w_2,...,w_{n-1}\} {w0​,w1​,w2​,...,wn−1​}，我们可以先计算只包含一个记录的序列的最优二叉查找树，然后在此基础上计算包含两个记录的序列的最优二叉查找树，然后以此类推计算包含多个记录的序列的最优二叉查找树。以这种方法来得到n个记录的最优二叉查找树。
     在算法实现上我们引入了两个二维数组$cost[n][n]$和$optimalRoot[n][n]$。$cost$数组的元素$cost[i][j]$，$0<=i<=j<=n-1$，存储在范围$[i,j]$内的记录构成的最优二叉查找树的带权路径长度，因此只需要计算包含主对角线以上的数组元素的值即可。$cost$数组主对角线上的元素$cost[i][i]$首先初始化为权值$freq[i]$。
     $optimalRoot$数组的元素$optimalRoot[i][j]$，$0<=i<=j<=n-1$，存储在范围$[i,j]$内的记录构成的最优二叉查找树的根节点对应的记录在原有序数组中的索引，因此只需要计算包含主对角线以上的数组元素的值即可。$optimalRoot$数组主对角线上的元素$optimalRoot[i][i]$首先初始化为i，因为这时的有序序列只有一个元素。一个简单的例子如图4所示。
     源代码参考于这里

　 图4.

class BinaryNode
{
public:
    BinaryNode(int value = 0, BinaryNode* left = nullptr, BinaryNode* right = nullptr)
    {
        key = value;
        leftChild = left;
        rightChild = right;
    }
    int getKey()
    {
        return key;
    }
    BinaryNode* getLeft()
    {
        return leftChild;
    }
    BinaryNode* getRight()
    {
        return rightChild;
    }
private:
    int key;
    BinaryNode* leftChild;
    BinaryNode* rightChild;
};

void traverseBinaryTree(BinaryNode* root)
{
    if (root != nullptr)
    {
        cout << "Node key is:" << root->getKey() << endl;
        traverseBinaryTree(root->getLeft());
        traverseBinaryTree(root->getRight());
    }
    else
    {
        cout << "root is nullptr!!!!" << endl;
        return;
    }
    return;
}

// A utility function to get sum of array elements  
// freq[i] to freq[j]  
int sum(int freq[], int i, int j);

/* A Dynamic Programming based function that calculates
minimum cost of a Binary Search Tree. */
int optimalSearchTree(int keys[], int freq[], int** optimalRoot,int n)
{
    /* Create an auxiliary 2D matrix to store results
    of subproblems */
    int** cost = new int*[n];
    for (int index=0;index<n;index++)
    {
        cost[index]= new int [n];
    }

    /* cost[i][j] = Optimal cost of binary search tree
    that can be formed from keys[i] to keys[j].
    cost[0][n-1] will store the resultant cost */

    // For a single key, cost is equal to frequency of the key  
    for (int i = 0; i < n; i++)
    {
        cost[i][i] = freq[i];
    }
    // Now we need to consider chains of length 2, 3, ... .  
    // L is chain length.  
    for (int L = 2; L <= n; L++)
    {
        // i is row number in cost[][]  
        for (int i = 0; i < n - L + 1; i++)
        {
            // Get column number j from row number i and  
            // chain length L  
            int j = i + L - 1;
            cost[i][j] = INT_MAX;

            // Try making all keys in interval keys[i..j] as root  
            for (int r = i; r <= j; r++)
            {
                // c = cost when keys[r] becomes root of this subtree  
                int c = ((r > i) ? cost[i][r - 1] : 0) +
                    ((r < j) ? cost[r + 1][j] : 0) +
                    sum(freq, i, j);
                if (c < cost[i][j])
                {
                    cost[i][j] = c;
                    optimalRoot[i][j] = r;
                }
            }
        }
    }
    return cost[0][n - 1];
}

// A utility function to get sum of array elements  
// freq[i] to freq[j]  
int sum(int freq[], int i, int j)
{
    int s = 0;
    for (int k = i; k <= j; k++)
        s += freq[k];
    return s;
}

void createOBST(BinaryNode* &root, int keys[],int** optimalRoot,int i,int j)
{
    BinaryNode* leftSubTree = nullptr;
    BinaryNode* rightSubTree = nullptr;
    // Base cases  
    if (j < i)  // no elements in this subarray  
    {
        return ;
    }

    if (j == i) // one element in this subarray  
    {
        root = new BinaryNode(keys[i], leftSubTree, rightSubTree);
        return ;
    }
    int rootIndex = optimalRoot[i][j];
    createOBST(leftSubTree, keys, optimalRoot, i, rootIndex-1);
    createOBST(rightSubTree, keys, optimalRoot, rootIndex + 1, j);
    
    root = new BinaryNode(keys[rootIndex], leftSubTree, rightSubTree);
    return ;
}

//测试程序
int main()
{
    int keys[] = { 10, 12, 20 };
    int freq[] = { 34, 8, 50 };
    int n = sizeof(keys) / sizeof(keys[0]);
    BinaryNode* root = nullptr;
    int** optimalRoot = new int* [n];
    for (int index = 0; index < n; index++)
    {
        optimalRoot[index] = new int[n];
    }
    for (int i = 0; i < n; i++)
    {
        optimalRoot[i][i] = i;
    }
    cout << "Cost of Optimal BST is:" << optimalSearchTree(keys, freq, optimalRoot,n)<<endl;


    for (int ki = 0; ki < n; ki++)
    {
        for (int kj = 0; kj < n; kj++)
        {
            cout << optimalRoot[ki][kj] << "            ";
        }
        cout << endl;
    }
    createOBST(root, keys, optimalRoot, 0, n-1);
    traverseBinaryTree(root);
    return 0;
}