在R语言中利用mice包进行缺失值的线性回归填补

在数据分析中，我们会经常遇到缺失值问题。一般的缺失值的处理方法有删除法和填补法。通过删除法，我们可以删除缺失数据的样本或者变量。而缺失值填补法又可分为单变量填补法和多变量填补法，其中单变量填补法又可分为随机填补法、中位数/中值填补法、回归填补法等。本文简单介绍一下如何在R语言中利用mice包对缺失值进行回归填补。

假设原始数据只有两列P（压力）和T（温度），具体数据如下：

orig_data <- data.frame(
  T = c(0.47, 0.45, 0.48, 0.47, 0.41, 0.56, 0.54, 0.51, 
        0.44, 0.56, NA, 0.62, 0.5, 0.43, NA, NA, 0.69, 
        0.73, 0.45, 0.43, 0.38, 0.35, 0.5, 0.46, 0.41, 
        0.43, 0.41, NA, 0.8, 0.51, NA, 0.44, NA, 0.43, 
        0.45, 0.77, 0.41, 0.77, 0.47, 0.63, 0.43, NA, NA, 
        0.47, NA, 0.25, 0.48, 0.49, 0.46, 0.72, NA, 0.36, NA, 
        0.45, 0.41, 0.36, 0.48, 0.4, 0.44, 0.73, 0.8, 0.45, 
        0.47, 0.54, 0.5, 0.5, 0.48, 0.44, NA, 0.42, 0.34, 
        0.45, NA, 0.42, 0.42, 0.42, 0.42, 0.52, 0.44, 0.56, 
        NA, 0.52, 0.44, 0.5, NA, 0.46, 0.42, 0.42, 0.35, 
        0.3, NA, 0.49, 0.53, 0.62, 0.48, 0.44, 0.48, 0.48, 
        0.45, 0.43, 0.43, 0.47, NA, 0.48, 0.69, 0.62, 0.45, 
        0.4, NA, 0.9, 0.7, 0.37, 0.66, 0.36, 0.76, 0.83, 0.44, 
        0.33, 0.46, 0.46, 0.43, 0.45, NA, 0.46, 0.43, 0.44, 
        0.52, 0.48, 0.44, 0.37, 0.47, 0.47),
  P = c(4650, 3720, 2050, 5600, 1420, 5299.6, 6714, 3858, 3731,
        3331, NA, 3800, 2190, 2800, NA, NA, 7135, 6817, 2264, 
        4490, 2359, 889, 3572, 4978, 3800, 1735, 2092, 4200, 
        6840, 2381, 250, 6637, NA, 1434, 3122, 11542, 1075, 
        12075, 5027, 3640, 2026, 4551, NA, 4551, NA, 927, 
        2727, 4400, 925, 10800, NA, 1894, 1514, 1987, 2741, 
        2788, 4490, 2375, 4772, 5490, 3190, 4177, 3490, 5660, 
        5750, 6220, 4345, 3983, 850, 4300, 2459, 2074, 2450, 
        3350, 3002, 3350, 3002, 1263, 2969, 827, NA, 5613, 3272,
        3360, 2600, 3599, 288, 653, 2062, 1300, NA, 4439, 4218, 
        4057, 1242, 4722, 2731, 3100, 2245, 2340, 3387, 2367, NA,
        6301, 3565, 9500, 9137, 2282, 2521, 11600, 7134, 2684, 
        4254, 1628, 5400, 6550, 3692, 2200, 980, 980, 1162, 3145, 
        NA, 2117, 3390, 4365, 800, 2250, 2915, 2929, 4229, 5830))

调用mice包的md函数可以看到原始数据中的缺失值模式。下表中1和0是缺失值模式：0表示变量中的列有缺失值，1表示没有缺失值。在原始数据中，P列缺失11个数据，T列缺失19个数据，两列数据都缺失的数据点有11个，两列数据都没有缺失的数据点有113个。我们还可以利用VIM包中的scattMiss()函数或者aggr()函数绘制缺失数据的散点图。

library(mice)
md.pattern(orig_data)
     	P  	T   
113  	1  	1  	0
  8 	 1  	0  	1
 11 	 0  	0  	2
    	11 	19 	30

library("VIM")  
aggr(orig_data, prop = T, numbers = T)

上述代码显示的缺失值分布图如下。从图中可以看出T数据列的缺失比例大约为14%（0.14），P列的缺失比例大约为8.3%，两列都缺失的数据占整个数据量的8.3%。

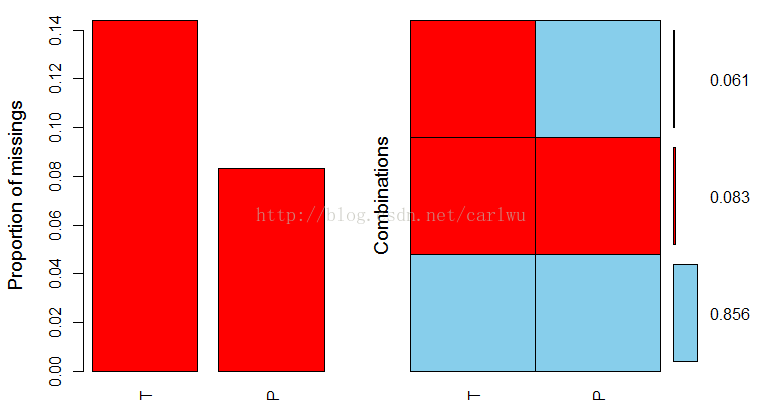
对于两个数据都缺失的 11个数据点，我们无法利用回归的方法对它们进行填补。但是对于有一个值缺失的数据点，我们可以利用回归填补法进行缺失值充填。因为P和T这个两个变量存在某种程度的线性相关。我们可以对这两个变量进行线性回归，以观察它们之间的线性关系。具体R代码如下。

plot(orig_data)
linear_model <- lm(P ~ T, data = orig_data)
abline(linear_model,col="red")
summary(linear_model)
上面代码输出结果如下。
Call:
lm(formula = P ~ T, data = orig_data)
Residuals:
    Min      1Q  Median      3Q     Max 
-4616.3 -1244.2    -2.6   766.6  5905.8 
Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)  -2651.1      712.2  -3.722 0.000312 ***
T            13071.9     1411.4   9.262 1.79e-15 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 1762 on 111 degrees of freedom
  (19 observations deleted due to missingness)
Multiple R-squared:  0.4359,	Adjusted R-squared:  0.4308 
F-statistic: 85.78 on 1 and 111 DF,  p-value: 1.79e-15

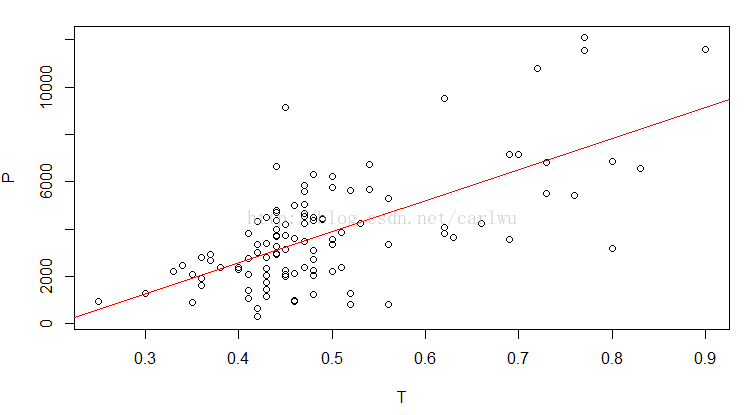
P和T进行线性回归后的R2为0.43。因此我们可以运行下面代码，利用线性回归方程对缺失的T值进行填补。

#首先加载sqldf包，将数据全部缺失的样本给排除掉
library(sqldf)
temp_data <-sqldf("select T, P from orig_data 
              where T is not null
              or P is not null",row.names=TRUE)

#利用mice包填补在T列的缺失值
imp <- mice(temp_data,seed=3231)
fit_new <- with(imp,linear_model )
pooled <- pool(fit_new)
#获得新生成的数据
new_data <- complete(imp,action=3)
#将原始数据和新数据进行并排比较
total_data <- cbind(temp_data,new_data)
colnames(total_data) <- c("original_T","original_P","new_T","new_P")
total_data

新产生的数据和原始的数据的比较结果如下：

    original_T original_P  new_T   new_P
1    0.47  4650.0       0.47     4650.0
2    0.45  3720.0       0.45     3720.0
3    0.48  2050.0       0.48     2050.0
4    0.47  5600.0       0.47     5600.0
5    0.41  1420.0       0.41     1420.0
6    0.56  5299.6       0.56     5299.6
7    0.54  6714.0       0.54     6714.0
8    0.51  3858.0       0.51     3858.0
9    0.44  3731.0       0.44     3731.0
10   0.56  3331.0       0.56     3331.0
11   0.62  3800.0       0.62     3800.0
12   0.50  2190.0       0.50     2190.0
13   0.43  2800.0       0.43     2800.0
14   0.69  7135.0       0.69     7135.0
15   0.73  6817.0       0.73     6817.0
16   0.45  2264.0       0.45     2264.0
17   0.43  4490.0       0.43     4490.0
18   0.38  2359.0       0.38     2359.0
19   0.35   889.0       0.35      889.0
20   0.50  3572.0       0.50     3572.0
21   0.46  4978.0       0.46     4978.0
22   0.41  3800.0       0.41     3800.0
23   0.43  1735.0       0.43     1735.0
24   0.41  2092.0       0.41     2092.0
25     NA  4200.0       0.47     4200.0
26   0.80  6840.0       0.80     6840.0
27   0.51  2381.0       0.51     2381.0
28     NA   250.0       0.35      250.0
29   0.44  6637.0       0.44     6637.0
30   0.43  1434.0       0.43     1434.0
31   0.45  3122.0       0.45     3122.0
32   0.77 11542.0       0.77    11542.0
33   0.41  1075.0       0.41     1075.0
34   0.77 12075.0       0.77    12075.0
35   0.47  5027.0       0.47     5027.0
36   0.63  3640.0       0.63     3640.0
37   0.43  2026.0       0.43     2026.0
38     NA  4551.0       0.44     4551.0
39   0.47  4551.0       0.47     4551.0
40   0.25   927.0       0.25      927.0
41   0.48  2727.0       0.48     2727.0
42   0.49  4400.0       0.49     4400.0
43   0.46   925.0       0.46      925.0
44   0.72 10800.0       0.72    10800.0
45   0.36  1894.0       0.36     1894.0
46     NA  1514.0       0.43     1514.0
47   0.45  1987.0       0.45     1987.0
48   0.41  2741.0       0.41     2741.0
49   0.36  2788.0       0.36     2788.0
50   0.48  4490.0       0.48     4490.0
51   0.40  2375.0       0.40     2375.0
52   0.44  4772.0       0.44     4772.0
53   0.73  5490.0       0.73     5490.0
54   0.80  3190.0       0.80     3190.0
55   0.45  4177.0       0.45     4177.0
56   0.47  3490.0       0.47     3490.0
57   0.54  5660.0       0.54     5660.0
58   0.50  5750.0       0.50     5750.0
59   0.50  6220.0       0.50     6220.0
60   0.48  4345.0       0.48     4345.0
61   0.44  3983.0       0.44     3983.0
62     NA   850.0       0.25      850.0
63   0.42  4300.0       0.42     4300.0
64   0.34  2459.0       0.34     2459.0
65   0.45  2074.0       0.45     2074.0
66     NA  2450.0       0.48     2450.0
67   0.42  3350.0       0.42     3350.0
68   0.42  3002.0       0.42     3002.0
69   0.42  3350.0       0.42     3350.0
70   0.42  3002.0       0.42     3002.0
71   0.52  1263.0       0.52     1263.0
72   0.44  2969.0       0.44     2969.0
73   0.56   827.0       0.56      827.0
74   0.52  5613.0       0.52     5613.0
75   0.44  3272.0       0.44     3272.0
76   0.50  3360.0       0.50     3360.0
77     NA  2600.0       0.43     2600.0
78   0.46  3599.0       0.46     3599.0
79   0.42   288.0       0.42      288.0
80   0.42   653.0       0.42      653.0
81   0.35  2062.0       0.35     2062.0
82   0.30  1300.0       0.30     1300.0
83   0.49  4439.0       0.49     4439.0
84   0.53  4218.0       0.53     4218.0
85   0.62  4057.0       0.62     4057.0
86   0.48  1242.0       0.48     1242.0
87   0.44  4722.0       0.44     4722.0
88   0.48  2731.0       0.48     2731.0
89   0.48  3100.0       0.48     3100.0
90   0.45  2245.0       0.45     2245.0
91   0.43  2340.0       0.43     2340.0
92   0.43  3387.0       0.43     3387.0
93   0.47  2367.0       0.47     2367.0
94   0.48  6301.0       0.48     6301.0
95   0.69  3565.0       0.69     3565.0
96   0.62  9500.0       0.62     9500.0
97   0.45  9137.0       0.45     9137.0
98   0.40  2282.0       0.40     2282.0
99     NA  2521.0       0.36     2521.0
100  0.90 11600.0       0.90    11600.0
101  0.70  7134.0       0.70     7134.0
102  0.37  2684.0       0.37     2684.0
103  0.66  4254.0       0.66     4254.0
104  0.36  1628.0       0.36     1628.0
105  0.76  5400.0       0.76     5400.0
106  0.83  6550.0       0.83     6550.0
107  0.44  3692.0       0.44     3692.0
108  0.33  2200.0       0.33     2200.0
109  0.46   980.0       0.46      980.0
110  0.46   980.0       0.46      980.0
111  0.43  1162.0       0.43     1162.0
112  0.45  3145.0       0.45     3145.0
113  0.46  2117.0       0.46     2117.0
114  0.43  3390.0       0.43     3390.0
115  0.44  4365.0       0.44     4365.0
116  0.52   800.0       0.52      800.0
117  0.48  2250.0       0.48     2250.0
118  0.44  2915.0       0.44     2915.0
119  0.37  2929.0       0.37     2929.0
120  0.47  4229.0       0.47     4229.0
121  0.47  5830.0       0.47     5830.0