PRML Chapter 03 Linear Models for Regression

最新推荐文章于 2022-03-02 01:14:21 发布

zhoudinglive

最新推荐文章于 2022-03-02 01:14:21 发布

阅读量475

点赞数 1

分类专栏： PRML读书笔记

本文链接：https://blog.csdn.net/carpentercc/article/details/82632209

版权

PRML读书笔记专栏收录该内容

9 篇文章 2 订阅

订阅专栏

PRML Chapter 03 Linear Models for Regression

本章主要介绍了监督学习中的基本模型——线性回归模型，即对给定的 $D$ 维输入，输出一个或者多个连续的目标变量 $t$ ，如第一章介绍的多项式拟合模型即是一种简单的线性回归模型。

Linear Basis Function Models

线性回归的最基本的模式定义如下，

y (x, ω) = ω 0 + ω 1 x 1 + . . . + ω D x D (3.1)

$y(\textit{x}, \mathbf{\omega})=\omega_0+\omega_1 x_1+...+\omega_D x_D \tag{3.1}$

如式(3.1)所示， $y(\textit{x}, \mathbf{\omega})$ 被定义为输入 $\textit{x}$ 的线性函数，这在很多时候都无法满足应用的需求，因为非线性显然是更常见的状态。因此，如果我们将式(3.1)中的输入 $\textit{x}$ 替换为输入的函数形式 $\phi(\textit{x})$ ，那么我们则可以得到以下扩展形式，

y (x, ω) = ω 0 + ω 1 ϕ 1 (x 1) + . . . + ω D ϕ D (x D) = ω 0 + \sum j = 1 D ω j ϕ j (x) (3.2)

$\begin{aligned} y(\textit{x}, \mathbf{\omega}) &=\omega_0+\omega_1 \phi_1(x_1)+...+\omega_D \phi_D(x_D) \\ & = \omega_0 + \sum_{j=1}^D \omega_j \phi_j(x) \end{aligned}\tag{3.2}$

式(3.2)中的函数 $\phi (\textit{x})$ 称为基函数，可以看到，通过使用非线性基函数， $y(\textit{x}, \mathbf{\omega})$ 能够表示为输入 $\textit{x}$ 的非线性函数。然而，我们之所以称式(3.2)为线性模型，是因为 $y(\textit{x}, \mathbf{\omega})$ 是参数 $\mathbf{\omega}$ 的线性函数。尽管式(3.2)具有较强的数据拟合能力，但其应用场景也极大的收到了其自身特性的约束，其主要局限性为，

容易造成维数灾难：因为我们假设式(3.2)中的基函数 $\phi (\textit{x})$ 在观测到任意数据前即确定，因此，当输入空间的维度 $D$ 较快增长时，基函数的数量通常随之成指数级增长；

一般地，我们常用的基函数形式有，

高斯基函数：其中 $\mu_j$ 控制了基函数在输入空间中的文职，参数 $s$ 控制了基函数的空间大小，

$\begin{matrix} (3.3) & ϕ_{j} (x) = e x p {- \frac{(x - μ_{j})^{2}}{2 s^{2}}} \end{matrix}$ $\phi_j(x) = exp \bigg{\{} -\frac{(x-\mu_j)^2}{2s^2} \bigg{\}} \tag{3.3}$
Sigmoid基函数：

$ϕ j (x) = σ {x - μ j s} (3.4)$ $\phi_j(x) = \sigma \bigg{\{} \frac{x-\mu_j}{s} \bigg{\}} \tag{3.4}$

其中 $\sigma(a)$ 是logistic sigmoid函数，定义为，

$σ (a) = 1 1 + e x p ( - a ) (3.5)$ $\sigma(a) = \frac{1}{1+exp(-a)} \tag{3.5}$

a. Maximum Likelihood and Least Squares

本节主要讨论了最大似然函数和最小化平方误差(最小二乘法)，首先进行概率建模，假设目标值 $t$ 由确定的函数 $y(\textit{x}, \mathbf{\omega})$ 给出，其定义如式(3.6)所示，

t = y (x, ω) + ϵ (3.6)

$t = y(\textit{x}, \mathbf{\omega}) + \epsilon \tag{3.6}$

其中，我们定义噪声 $\epsilon$ 是一个零均值的高斯随机变量，精度(方差的倒数)为 $\beta$ ，我们可以使用模型式(3.6)中的右侧预测值 $y(\textit{x}, \mathbf{\omega}) + \epsilon$ 的分布来描述左侧目标值 $t$ ，因此我们有，

\begin{matrix} (3.7) & p (t | x, ω, β) = N (t | y (x, ω), β^{- 1}) \end{matrix}

$p(t|\textit{x}, \mathbf{\omega}, \beta) = \mathcal{N}(t|y(\textit{x}, \mathbf{\omega}), \beta^{-1} \tag{3.7})$

考虑式(3.7)的最大似然形式，定义输入数据集 $\textbf{X}=\{x_1, x_2, ..., x_N\}$ ，对应的目标值为 $t_1, t_2, ... t_N$ ，我们把目标向量 $\{t_n\}$ 记作 $\textbf{t}$ ，则有，

p (t | X, ω, β) = \prod n = 1 N  (t n | ω T ϕ (x n), β - 1) (3.8)

$p(\textbf{t}|\textbf{X}, \mathbf{\omega}, \beta) = \prod_{n=1}^N \mathcal{N}(t_n | \mathbf{\omega}^T\phi(x_n), \beta^{-1}) \tag{3.8}$

对式(3.8)取对数，可以得到，

l n p (t | ω, β) = \sum n = 1 N  (t n | ω T ϕ (x n), β - 1) = N 2 l n β - N 2 l n (2 π) - β E D (ω) (3.9)

$\begin{aligned} ln p(\textbf{t}|\mathbf{\omega}, \beta) &= \sum_{n=1}^N \mathcal{N}(t_n|\mathbf{\omega}^T\phi(x_n),\beta^{-1}) \\ & = \frac{N}{2}ln \beta -\frac{N}{2}ln(2\pi)-\beta E_D(\omega) \end{aligned}\tag{3.9}$

其中 $E_D$ 为平方和误差函数，我们也可以从式(3.8)和(3.9)中看出，线性回归模型在噪声均值为零的情况下，其最大似然等于最小平方误差，

E D (ω) = 1 2 \sum n = 1 N {t n - ω T ϕ (x)} 2 (3.10)

$E_D(\omega) = \frac{1}{2}\sum_{n=1}^N\big{\{} t_n - \omega^T\phi(x) \big{\}}^2 \tag{3.10}$

得到最大对数似然的公式(3.8)后，我们则可以通过对参数进行求偏导得到参数的解有，

ω M L = (Φ T Φ) - 1 Φ T t 1 β M L = 1 N \sum n = 1 N {t n - ω T M L ϕ (x n)} 2 (3.11) (3.12)

$\begin{gather} \omega_{ML} = (\mathbf{\Phi}^T\mathbf{\Phi})^{-1}\mathbf{\Phi}^T\textbf{t} \tag{3.11} \\ \frac{1}{\beta_{ML}} = \frac{1}{N}\sum_{n=1}^N \big{\{} t_n -\omega_{ML}^T\phi(x_n) \big{\}}^2 \tag{3.12} \end{gather}$

其中 $\mathbf{\Phi}$ 定义为一个 $N * M$ 的矩阵，称为设计矩阵(design matrix)，

⎡ ⎣ ⎢ ⎢ ⎢ ϕ 0 (x 1) ⋮ ϕ 0 (x N) \dots ⋱ \dots ϕ M - 1 (x 1) ⋮ ϕ M - 1 (x N) ⎤ ⎦ ⎥ ⎥ ⎥ (3.13)

$\begin{bmatrix} \phi_0(x_1) & \cdots & \phi_{M-1}(x_1) \\ \vdots & \ddots & \vdots \\ \phi_0(x_N) & \cdots & \phi_{M-1}(x_N) \end{bmatrix} \tag{3.13}$

若式(3.6)对偏置 $\omega_0$ 求偏导，我们可以将式(3.10)演化为式(3.14)，

E D (ω) = 1 2 \sum n = 1 N {t n - ω 0 - \sum j = 1 M - 1 ω j ϕ j (x n)} 2 (3.14)

$E_D(\omega) = \frac{1}{2}\sum_{n=1}^N \{t_n-\omega_0-\sum_{j=1}^{M-1}\omega_j \phi_j(x_n)\}^2 \tag{3.14}$

并对偏置 $\omega_0$ 求偏导，得到，

ω 0 = t ¯ - \sum j = 1 M - 1 ω j ϕ ¯ j t ¯ = 1 N \sum n = 1 N t n ϕ ¯ j = 1 N \sum n = 1 N ϕ j (x n) (3.15) (3.16) (3.17)

$\begin{gather} \omega_0 = \bar{t} - \sum_{j=1}^{M-1}\omega_j\bar{\phi}_j \tag{3.15}\\ \bar{t}=\frac{1}{N}\sum_{n=1}^Nt_n \tag{3.16} \\ \bar{\phi}_j=\frac{1}{N}\sum_{n=1}^N\phi_j(x_n) \tag{3.17} \end{gather}$

从式(3.15)至(3.17)可以看出，偏置的主要作用是补偿训练集上目标值的均值和基函数均值的加权平均之间的差值。

b. Geometry of least squares

从几何角度看最小平方和误差(最小二乘法)，可以考虑一个 $N$ 维空间，它的坐标轴由 $t_n$ 给出，即 $\textbf{t}=\{t_1...t_N\}^T$ 是这个空间中的一个向量。对于每一个具有 $M$ 个基函数 $\phi(x)$ 的线性回归模型 $y(\textit{x}, \mathbf{\omega})$ ，其可以看作是一个在 $N$ 维空间中的 $M$ 维子空间 $S$ ，因此，函数 $y(\textit{x}, \mathbf{\omega})$ 表示子空间 $S$ 中的任意位置。如果把子空间 $S$ 看作回归函数的预测值空间，而将 $N$ 维 $t$ 坐标空间视为目标值空间，则最小平方和误差的目标则是寻找与目标值空间中的目标向量 $\textbf{t}$ 最近的预测值空间中的预测向量 $y$ 。

如下图所示，我们要在子空间 $S$ 中寻找使得距离 $t$ 最近的参数 $\mathbf{\omega}$ ，一般地，我们认为 $t$ 在子空间 $S$ 上的正交投影为 $\mathbf{\omega}$ 的解。

![这里写图片描述](https://img-blog.csdn.net/20180912170230743?watermark/2/text/aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L2NhcnBlbnRlcmNj/font/5a6L5L2T/fontsize/400/fill/I0JBQkFCMA==/dissolve/70)

c. Sequential learning

与第二章介绍的一样，顺序学习的主要目的还是解决实时应用与一次计算量过大的问题，这里我们可以选择一个数据点或者一小部分数据点，运用随机梯度下降(stochastic gradient descent)的技术，实现参数的迭代更新。如果误差函数由数据点的和 $E=\sum_n E_n$ 组成，那么使用随机梯度下降实现的参数顺序学习如下所示，

ω (τ + 1) = ω (τ) - η \nabla E n (3.18)

$\omega^{(\tau + 1)} = \omega^{(\tau)} - \eta \nabla E_n \tag{3.18}$

对于如式(3.10)所示的最小平方和误差函数，我们可以获得如下形式的推导，

ω (τ + 1) = ω (τ) + η (t n - ω (τ) T ϕ n) ϕ n (3.19)

$\omega^{(\tau + 1)} = \omega^{(\tau)} + \eta (t_n - \omega^{(\tau)T}\phi_n)\phi_n \tag{3.19}$

d. Regularized least squares

最大似然估计在数据量较小的情况下容易造成过拟合的问题在线性回归模型上仍然存在，因此为了降低这种情况，我们使用正则化项，也就是第一章中的惩罚项。即我们可以将误差函数的形式定义为，

E D (ω) + λ E W (ω) (3.20)

$E_D (\omega) + \lambda E_W (\omega) \tag{3.20}$

考虑平方和误差则有如下形式，

1 2 \sum n = 1 N {t n - ω T ϕ (x n)} 2 + λ 2 ω T ω (3.21)

$\frac{1}{2} \sum_{n=1}^N \{t_n - \omega^T\phi(x_n)\}^2 + \frac{\lambda}{2}\omega^T \omega \tag{3.21}$

对式(3.21)对参数 $\omega$ 求偏导，可以得到参数的解，

ω = (λ I + Φ T Φ) - 1 Φ T t (3.22)

$\omega = (\lambda I + \Phi^T\Phi)^{-1}\Phi^T \textbf{t} \tag{3.22}$

与式(3.11)进行相应的比较，会发现式(3.22)多了一个 $\lambda$ ，即同样是最小化误差函数，加入了正则项后，由于权值 $\lambda$ 的作用，会导致基函数 $\phi$ 的复杂性大大降低，进而实现对过拟合的降低。

e. Multiple outputs

对于多元目标值，一般会有两种想法，假设对于 $K$ 元目标值( $K > 0$ )，

方案一：对于 $K$ 元目标向量中的每一个分量，引入一个不同的基函数集合，即 $y_i(\textit{x}, \mathbf{\omega}), i \in 1, ..., K$ ，这样就变成了多个独立的线性回归问题；
方案二：与方案一不同，方案二中对于所有的分量使用相同的基函数集合，而使用不同的参数，具体的定义 $y$ 是一个 $K$ 维的列向量，定义参数 $\textbf{W}$ 式一个 $M * K$ 的向量(对于目标向量的每一个维度，有不同的 $M$ 个参数)，而基函数 $\phi(x)$ 是一个 $M$ 维的列向量，每个元素为 $\phi_j(x)$ ，其中 $\phi_0(x) = 1$ ，则我们可以有如下的线性回归函数形式，

$y (x, ω) = W T ϕ (x) (3.23)$ $y(x, \omega) = \textbf{W}^T\phi(x) \tag{3.23}$

The Bias-Variance Decomposition

Linear Basis Function Models部分讲到的线性回归模型，在现实的应用中往往具有很高的局限性，其主要表现在以下几个方面，

最大似然函数的通病，即在有限规模的数据集上训练复杂模型时，容易造成过拟合的现象；
在线性回归函数训练前，通常都指定了基函数的形式和数量，这很大程度上限制了线性回归模型描述数据中有趣的规律的灵活性；
使用正则化项来控制过拟合的主要问题时如何选择正确的正则化系数 $\lambda$ ，从而pick出函数空间中中等复杂程度的模型。

a. Background

因此，为了进一步解决以上线性回归模型的以上三个问题，频率学派和贝叶斯学派分别提出了自己的方法，本节介绍的偏置-方差折中法(bias-variance trade-off)即是一种频率学派的解决办法。

在第二章决策论部分，我们定义了损失函数(loss function)为 $L(t, y(\textbf{x}))$ ，并且采用损失函数的期望式(3.24)来选择最优的模型，

E [L] = \iint L (t, y (x)) p (x, t) d x d t (3.24)

$E[L]= \iint L(t, y(\textbf{x}))p(\textbf{x}, t)d\textbf{x}dt \tag{3.24}$

以使用平方损失函数为例，即 $L(t, y(\textbf{x}))=\{y(\textbf{x})-t\}^2$ ，对误差函数的期望求偏导，可以得到最优的函数模型 $h(x)$ ，具体推导如下，

E [L] = \iint {y (x) - t} 2 p (x, t) d x d t \Rightarrow δ E [ L ] δ y ( x ) = 2 \int {y (x) - t} p (x, t) d t = 0 \Rightarrow h (x) = \int t p ( x , t ) d t p ( x ) = \int t p (t | x) d t = E t [t | x] (3.25) (3.26) (3.27)

$\begin{gather} E[L] = \iint{\{y(\textbf{x})-t\}^2}p(\textbf{x},t)d\textbf{x}dt \tag{3.25}\\ \Rightarrow \frac{\delta E[L]}{\delta y(\textbf{x})} = 2\int \{y(\textbf{x})-t\}p(\textbf{x}, t)dt=0 \tag{3.26}\\ \Rightarrow h(\textbf{x}) = \frac{\int tp(\textbf{x},t)dt}{p(\textbf{x})}=\int tp(t|\textbf{x})dt=E_t[t|\textbf{x}] \tag{3.27} \end{gather}$

因此，当我们知道了条件概率分布 $p(t|\textbf{x})$ 后，损失函数即能给出最优的预测结果，如式(3.27)所示。我们可以对式(3.25)的平方项做一些处理，进而得到偏置-方差折中法，

{y (x) - t} 2 = {y (x) - E [t | x] + E [t | x] - t} 2 = {y (x) - E [t | x]} 2 + 2 {y (x) - E [t | x]} {E [t | x] - t} + {E [t | x] - t} 2 (3.28)

$\begin{aligned} \{y(\textbf{x}) - t\}^2 &= \{y(\textbf{x}) - E[t|\textbf{x}] + E[t|\textbf{x}]- t\}^2 \\ &= \{y(\textbf{x}) - E[t|\textbf{x}]\}^2 + 2\{y(\textbf{x}) - E[t|\textbf{x}] \}\{E[t|\textbf{x}]-t\}+\{E[t|\textbf{x}]-t\}^2 \end{aligned}\tag{3.28}$

式(3.28)是对式(3.25)中平方项的一个简单的扩展，将式(3.28)代入式(3.25)可以得到式(3.29)，交叉项在积分的过程中被消掉，

E [{y (x) - t} 2] = \int {y (x) - h (x)} 2 p (x) d x + \iint (h (x) - t) 2 p (x, t) d x d t (3.29)

$E[\{y(\textbf{x})-t\}^2] = \int \{ y(\textbf{x}) - h(\textbf{x})\}^2p(\textbf{x})d\textbf{x}+\iint(h(\textbf{x})-t)^2p(\textbf{x},t)d\textbf{x}dt \tag{3.29}$

上式可以看作是预测函数 $y(\textbf{x})$ 与最优函数 $h(\textbf{x})$ 之间的偏差(即两者之间的相似程度)，加上最优函数与目标值之间的方差(即最优函数在目标值附近的波动)。

b. Bias-variance trade-off

对于偏置-方差折中法，一般考虑使用参数 $\omega$ 控制的函数 $y(x,\omega)$ 对 $h(x)$ 建模，

贝叶斯学派：从贝叶斯的观点来看，模型 $y(x,\omega)$ 的不确定性由 $\omega$ 的后验概率分布来确定，因此会对利用到整个 $\omega$ 的分布；
频率学派：从频率学家的角度看，主要是利用数据集 $\mathcal{D}$ 对参数 $\omega$ 进行点估计，在具有多个数据集 $\mathcal{D}$ 的情况下，对每一个数据集训练出一个函数和其相应的平方损失值，对所有的数据集上得到的函数进行平均来评估模型。

从以上两派人马的观点可以看出，其核心思想都是通过平均来降低过拟合的程度，贝叶斯利用的是参数 $\omega$ 的平均，而频率观点采用数据集上的平均。因此，与式(3.29)类似，对应于每一个数据集 $\mathcal{D}$ 有，

E D [{y (x; ) - h (x)} 2] = {E D [y (x; )] - h (x)} 2              (b a i s) 2 + E D [{y (x; ) - E D [y (x, )]} 2]                    v a r i a n c e (3.30)

$\begin{aligned} E_D[\{y(x;\mathcal{D})-h(x)\}^2] &= \begin{matrix} \underbrace{\{ E_D[y(x;\mathcal{D})]-h(x) \}^2} \\ (bais)^2\end{matrix} + \begin{matrix} \underbrace{ E_D[\{y(x;\mathcal{D}) - E_D[y(x,\mathcal{D})]\}^2]} \\ variance \end{matrix} \end{aligned} \tag{3.30}$

对比式(3.29)和(3.30)，(3.30)无非就是对多个数据集进行了一下平均。式(3.30)的第一项表示所有数据集得出的平均预测与最优模型 $h(x)$ 之间的差异即平方偏置(bias)；第二项则度量了对于单个数据集，单个模型给出的解在平均值附近的波动，这被称为方差(variance)。

现在我们可以看一下式(3.30)用以降低过拟合的原理，对于数据集上的损失均值(3.30)，很显然，我们的目标是要使其最小化，

情况一：当偏差趋近于零时，意味着各数据集上训练得到的模型平均后与最优模型基本吻合，这时往往就是过拟合了，方差部分因为过拟合的模型无法拟合每一个数据集，因此便会产生较大的损失，造成式(3.30)无法达到最小值；
情况二：当方差趋近于零时，意味着每一个数据集上训练得到的模型都差别不大，这显然是发生了欠拟合，因此偏差就会成倍增加。

综合以上两种极端情况，可以看出偏置-方差折中的原理，即通过最小化约束来互相惩罚。然而这一方法也具有很大的局限性，主要表现在其依赖于所有数据集的平均，而实际应用中，往往不存在多个数据集，即使存在也会对其合并，使用更大规模的数据训练复杂模型效果会更好。

Bayesian Regression Model

基于以上传统的最大似然的局限性，贝叶斯方法通常是引入参数的先验分布，并利用贝叶斯定理计算后验分布在先验分布上的平均，从而解决，

问题一：使用最大似然的线性回归模型，往往需要根据特定的应用确定合适的模型复杂度的问题；
问题二：最大似然函数的过拟合问题；
问题三：降低因引入正则项而增加的计算量。

a. Parameter distribution

在偏置-方差折中的方法里，主要考虑的是预测函数 $y(\textbf{x},\omega)$ 中参数 $\omega$ 的点估计，而贝叶斯方法考虑参数 $\omega$ 的全分布，因此，我们可以定义参数 $\omega$ 服从均值为 $m_0$ 、协方差 $\textbf{S}_0$ 的高斯分布，

p (ω) =  (ω | m 0, S 0) (3.31)

$p(\omega)=\mathcal{N}(\omega|m_0, \textbf{S}_0) \tag{3.31}$

给定数据集的目标值 $\textbf{t}$ ，我们在式(3.7)定义了似然函数 $p(\textbf{t}|\omega)$ ，进而可以得到相应的后验分布，

p (ω | t) =  (ω | m N, S N) m N = S N (S - 1 0 m 0 + β Φ T t) S - 1 N = S - 1 0 + β Φ T Φ (3.32) (3.33) (3.34)

$\begin{gather} p(\omega|\textbf{t})=\mathcal{N}(\omega|m_N,\textbf{S}_N) \tag{3.32} \\ m_N = \textbf{S}_N(\textbf{S}_0^{-1}m_0+\beta \mathbf{\Phi}^T\textbf{t}) \tag{3.33} \\ \textbf{S}_N^{-1}=\textbf{S}_0^{-1}+\beta \mathbf{\Phi}^T\mathbf{\Phi} \tag{3.34} \end{gather}$

以上即为基于贝叶斯方法的线性回归函数参数分布的基本形式，在PRML中，为了简化讨论，考虑参数分布为均值为零的高斯分布，并且分布由精度参数 $\alpha$ 控制，

p (ω | α) =  (ω | 0, α - 1 I) (3.35)

$p(\omega|\alpha)=\mathcal{N}(\omega| 0, \alpha^{-1}I) \tag{3.35}$

这样后验分布中 $m_N、\textbf{S}_N^{-1}$ 也会发生相应的变化。考虑后验分布(3.32)的最大似然，我们称之为最大后验分布(Maximum A Posteriori)，对其取对数的结果如下，

l n p (ω | t) = - β 2 \sum n = 1 N {t n - ω T ϕ (x n)} 2 - α 2 ω T ω + c o n s t (3.34)

$ln p(\omega|\textbf{t})=-\frac{\beta}{2}\sum_{n=1}^N\{t_n-\omega^T\phi(x_n)\}^2-\frac{\alpha}{2}\omega^T\omega+const \tag{3.34}$

将式(3.34)与基于最大似然估计的式(3.14)相比，会发现最大后验比最大似然多了一个参数 $\omega$ 的二次项，这显然与加入正则项的最大似然一致。

b. Predictive distribution

在实际应用中，更常用到的是预测分布，即给定新的输入值 $\boldsymbol{x}$ 预测出新的 $t$ ，其具体形式如下，

\begin{matrix} (3.35) & p (t | t, α, β) = \int p (t | ω, β) p (ω | t, α, β) d ω \end{matrix}

$p(t|\textbf{t},\alpha,\beta) = \int p(t|\omega, \beta)p(\omega|\textbf{t},\alpha,\beta)d\omega \tag{3.35}$

参数	含义
$\textbf{t}$	训练数据集中的目标值集合
$\alpha$	参数 $\omega$ 的控制参数，来自先验(3.35)
$\beta$	似然函数(3.7)的控制参数，定义为高斯分布的精度

$\\$

因为式(3.57)中的两项均为高斯分布，因此我们可以把预测分布表示为，

p (t | x, t, α, β) =  (t | m T N ϕ (x), σ 2 N (x)) δ 2 N (x) = 1 β + ϕ (x) T S N ϕ (x) (3.36) (3.37)

$\begin{gather} p(t|\boldsymbol{x},\textbf{t},\alpha,\beta)=\mathcal{N}(t|m_N^T\phi(\boldsymbol{x}),\sigma_N^2(\boldsymbol{x})) \tag{3.36} \\ \delta_N^2(\boldsymbol{x})=\frac{1}{\beta}+\phi(\boldsymbol{x})^T\textbf{S}_N\phi(\boldsymbol{x}) \tag{3.37} \end{gather}$

式(3.37)中的第一项取自似然函数(3.7)，被定义为精度，可以看作是数据中的噪声；第二项与先验(3.35)有关，其反映了预测分布与参数 $\omega$ 关联的不确定性。很显然的，当我们观测到足够多的数据时，预测分布的结果与最大似然类似，这样，我们的先验起的作用将很小，即式(3.37)仅仅只由数据中的噪声 $\beta$ 控制。

c. Equivalent kernel

等价核可以看作一种非参数的训练方法。考虑式(3.33)，如果采用零均值先验的参数分布即 $m_0=0$ ，则式(3.33)变为，

m N = β S N Φ t (3.38)

$m_N = \beta \textbf{S}_N\mathbf{\Phi}\textbf{t} \tag{3.38}$

将式(3.38)代入式(3.2)，则有，

y (x, m N) = m T N ϕ (x) = \sum n = 1 N β ϕ (x) T S N ϕ (x n) t n (3.39)

$\begin{aligned} y(\boldsymbol{x},\boldsymbol{m}_N) &= \boldsymbol{m}_N^T\boldsymbol{\phi}(\boldsymbol{x}) \\ &= \sum_{n=1}^N \beta \boldsymbol{\phi}(x)^T\textbf{S}_N\boldsymbol{\phi}(\boldsymbol{x}_n)t_n \end{aligned}\tag{3.39}$

其中 $\textbf{S}_N$ 由式(3.34)定义，因此在点 $\boldsymbol{x}$ 处的预测均值由训练机目标变量 $t_n$ 的线性组合给出，

y (x, m N) = \sum n = 1 N k (x, x n) t n k (x, x n) = β ϕ (x) T S N ϕ (x') (3.40) (3.41)

$\begin{gather} y(\boldsymbol{x},\boldsymbol{m}_N) = \sum_{n=1}^N k(\boldsymbol{x}, \boldsymbol{x}_n)t_n \tag{3.40} \\ k(\boldsymbol{x}, \boldsymbol{x}_n) = \beta \boldsymbol{\phi}(\boldsymbol{x})^T\textbf{S}_N \boldsymbol{\phi}(\boldsymbol{x}') \tag{3.41} \end{gather}$

式(3.41)的 $k(\boldsymbol{x}, \boldsymbol{x}_n)$ 函数被称为平滑矩阵(smoother matrix)或者等价核(equivalent kernel)。对于式(3.40)，我们可以认为等价核描述的是新输入值 $\boldsymbol{x}$ 与已有数据集中数据点 $\boldsymbol{x}_n$ 之间的距离，而 $y(\boldsymbol{x},\boldsymbol{m}_N)$ 则是数据点的目标值 $t_n$ 与这一距离的加权平均。比较常见的方法比如 $K$ 最近邻。

Bayesian Model Comparison

贝叶斯模型比较(Bayesian Model Comparison)是贝叶斯学派看待模型复杂度的方法论，即通过概率来表示模型选择的不确定性，对每一个模型，利用其整个参数分布上对数据集的拟合程度反应其优先级。假设我们有 $L$ 个模型 $\{\mathcal{M}_i\}$ ，其中 $i=1,...,L$ 。对于给定数据集 $\mathcal{D}$ 和模型的先验 $p(\mathcal{M}_i)$ ，我们定义其后验分布为，

p ( i | ) \propto p ( i) p ( |  i) (3.42)

$p(\mathcal{M}_i|\mathcal{D}) \propto p(\mathcal{M}_i)p(\mathcal{D}|\mathcal{M}_i) \tag{3.42}$

对于式(3.42)，先验分布 $p(\mathcal{M}_i)$ 用于描述不同模型之间的优先级。模型证据(model evidence) $p(\mathcal{D}|\mathcal{M}_i)$ ，可以看作是模型空间上的似然函数，因此也被称为边缘似然(marginal likelihood)，它表达了考虑数据拟合能力后的模型优先级，描述了从一个模型生成一个数据集 $\mathcal{D}$ 的概率。

模型选择(model selection)：对于模型求平均来选择模型可以简单的近似为使用最有可能的一个模型作为预测。

这里写图片描述

使用以上的模型选择思想，可以对模型证据进行相应的近似选择，考虑使用一个参数 $\omega$ 控制模型证据，

p ( |  i) = \int p ( | ω,  i) p (ω |  i) d ω (3.43)

$p(\mathcal{D}|\mathcal{M}_i) = \int{p(\mathcal{D}|\omega,\mathcal{M}_i)}p(\omega|\mathcal{M}_i) d\omega\tag{3.43}$

通过考虑参数 $\omega$ 的近似，我们可以更清楚的认识到模型证据的性质并选择出更优的模型，

p (ω | ,  i) = p (  | ω ,  i ) p ( ω |  i ) p (  |  i ) (3.45)

$p(\omega|\mathcal{D}, \mathcal{M}_i) = \frac{p({\mathcal{D}|\omega,\mathcal{M}_i)p(\omega|\mathcal{M}_i)}}{p(\mathcal{D|\mathcal{M}_i})} \tag{3.45}$

考虑每一个模型仅有一个参数 $\omega$ ，由式(3.5)可知 $p(\omega|\mathcal{D}, \mathcal{M}_i) \propto p({\mathcal{D}|\omega,\mathcal{M}_i)p(\omega|\mathcal{M}_i)}$ ，对于似然函数 $p({\mathcal{D}|\omega,\mathcal{M}_i)}$ ，我们考虑使用最有可能的 $\omega_{MAP}$ 来近似，

\int p ( | ω,  i) d ω ≃ p ( | ω M A P,  i) * Δ ω p o s t e r i o r i (3.46)

$\int p({\mathcal{D}|\omega,\mathcal{M}_i)}d\omega \simeq p(\mathcal{D}|\omega_{MAP},\mathcal{M}_i) * \Delta \omega_{posteriori} \tag{3.46}$

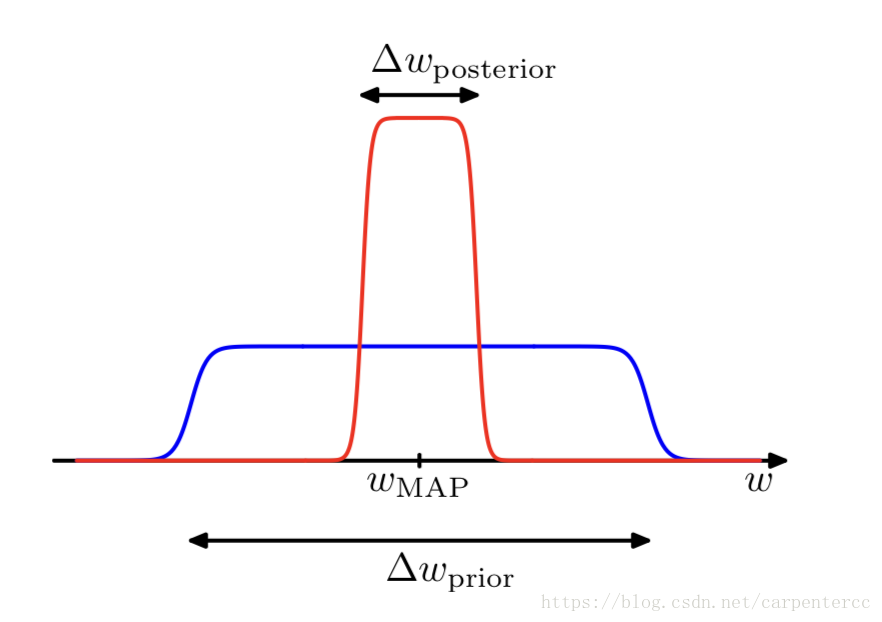
如图所示，式(3.46)对 $\omega$ 的积分近似为对尖峰 $\omega_{MAP}$ 与 $\Delta \omega_{posterior}$ 的乘积。类似地，我们可以对先验分布 $p(\omega|\mathcal{M}_i)$ 进行相同的近似，对于平坦的宽度为 $\Delta \omega_{prior}$ 的先验分布，其 $p(\omega|\mathcal{M}_i)=\frac{1}{\Delta \omega_{prior}}$ ，因此式(3.43)可以表示为，式(3.44)简化了所有的 $\mathcal{M}_i$ ，

p () = \int p ( | ω) p (ω) d ω ≃ 1 Δ ω p r i o r \int p ( | ω) d ω ≃ p ( | ω M A P) * Δ ω p o s t e r i o r Δ ω p r i o r (3.47)

$\begin{aligned} p(\mathcal{D}) &= \int p(\mathcal{D}|\omega)p(\omega)d\omega \simeq \frac{1}{\Delta \omega_{prior}} \int p(\mathcal{D|\omega})d\omega \\ & \simeq p(\mathcal{D}|\omega_{MAP}) * \frac{\Delta \omega_{posterior}}{\Delta \omega_{prior}} \end{aligned} \tag{3.47}$

对式(3.47)求对数可以得到，

l n p () ≃ l n p ( | ω M A P) + l n (Δ ω p o s t e r i o r Δ ω p r i o r) (3.48)

$ln p(\mathcal{D}) \simeq ln p(\mathcal{D}|\omega_{MAP}) + ln\bigg{(} \frac{\Delta \omega_{posterior}}{\Delta \omega_{prior}} \bigg{)} \tag{3.48}$

类似地，对于多个参数( $M > 0$ )，有

l n p () ≃ l n p ( | ω M A P) + M * l n (Δ ω p o s t e r i o r Δ ω p r i o r) (3.49)

$ln p(\mathcal{D}) \simeq ln p(\mathcal{D}|\omega_{MAP}) + M * ln\bigg{(} \frac{\Delta \omega_{posterior}}{\Delta \omega_{prior}} \bigg{)} \tag{3.49}$

对于式(3.48)和式(3.49)中的第一项可以理解为最优参数下模型对于数据的拟合程度，而第二项作为惩罚项，当 $\Delta \omega_{posterior}$ 变小时，即参数更加接近数据时， $ln\bigg{(} \frac{\Delta \omega_{posterior}}{\Delta \omega_{prior}} \bigg{)}$ 会变成一个很小的负数，从而达到惩罚的效果，显然，我们的目标是最大化(3.48)或者(3.49)，即最大化模型对数据的拟合程度。

以上便是从贝叶斯角度，对模型复杂度的理解，以及模型选择中对过拟合的判别。

The Evidence Approximation

a. Evaluation of the evidence function

纯粹的贝叶斯处理方法中，通常会引入超参数 $\alpha$ 和 $\beta$ 的先验分布，然后通过对超参数以及参数 $\omega$ 求积分的方式做预测。但实际情况是，我们可以解析的求出对参数 $\omega$ 的积分，或者解析的求出对参数 $\alpha$ 、 $\beta$ 的积分；却无法对所有的这些参数解析的求得，因此，定义一种近似方法，

证据近似(evidence approximation)：首先获取到超参数的近似形式，再利用该近似对参数 $\omega$ 求积分。证据近似在统计学的文献中也被称为经验贝叶斯(empriccal Bayes)、第二类最大似然(type2 maximum likelihood)、或者推广的最大似然(generalized maximum likelihood)。

如果引入 $\alpha$ 和 $\beta$ 的超参数先验分布，那么预测分布可以通过 $\omega、\alpha、\beta$ 求积分的方式获得，式(3.50)省略了对输入 $x$ 的以来， $\boldsymbol{t}$ 表示多个样本的目标值 $t$ ，而 $\textbf{t}$ 表示一个样本的多元目标值，

p (t | t) = ∭ p (t | ω, β) p (ω | t, α, β) p (α, β | t) d ω d α d β (3.50)

$p(t|\textbf{t}) = \iiint p(t|\boldsymbol{\omega},\beta)p(\omega|\textbf{t},\alpha,\beta)p(\alpha,\beta|\textbf{t})d\boldsymbol{\omega}d\alpha d\beta \tag{3.50}$

由于无法解析的求得所有参数的解，证据近似的方法告诉我们可以找到后验分布 $p(\alpha,\beta|\textbf{t})$ 的近似解 $\hat{\alpha}$ 和 $\hat{\beta}$ ，由此，式(3.50)表示的预测分布就可以近似为，

p (t | t) ≃ p (t | t, α ̂, β ̂) = \int p (t | ω, β ̂) p (ω | t, α ̂, β ̂) d ω (3.51)

$\begin{aligned} p(t|\textbf{t}) &\simeq p(t|\textbf{t},\hat{\alpha},\hat{\beta}) \\ &= \int p(t|\boldsymbol{\omega},\hat{\beta})p(\boldsymbol{\omega}|\textbf{t},\hat{\alpha},\hat{\beta})d\boldsymbol{\omega} \end{aligned} \tag{3.51}$

因此，我们只需要求得 $\alpha$ 、 $\beta$ 的近似 $\hat{\alpha}$ 、 $\hat{\beta}$ 即可，而由贝叶斯定理可知， $p(\alpha,\beta|\textbf{t})$ 服从，

p (α, β | t) \propto p (t | α, β) p (α, β) (3.52)

$p(\alpha, \beta|\textbf{t}) \propto p(\textbf{t}|\alpha,\beta)p(\alpha,\beta) \tag{3.52}$

在证据框架中，我们可以通过最大化边缘似然函数 $p(\textbf{t}|\alpha,\beta)$ 得到 $\hat{\alpha}$ 、 $\hat{\beta}$ 。

对于边缘似然分布 $p(\textbf{t}|\alpha, \beta)$ ，通过全职参数进行积分可以得到，即

p (t | α, β) = \int p (t | ω, β) p (ω | α) d ω (3.53)

$p(\textbf{t}|\alpha, \beta) = \int p(\textbf{t}|\boldsymbol{\omega}, \beta)p(\boldsymbol{\omega}|\alpha)d\omega \tag{3.53}$

对于线性回归模型，由式(3.9)、(3.10)、(3.35)可得，

p (t | α, β) = (β 2 π) N 2 (α 2 π) M 2 π \int e x p {- E (ω)} d ω (3.54)

$p(\textbf{t}|\alpha,\beta)=\bigg{(} \frac{\beta}{2\pi} \bigg{)}^{\frac{N}{2}} \big{(} \frac{\alpha}{2\pi} \big{)}^{\frac{M}{2\pi}}\int exp\{ -E(\boldsymbol{\omega})\} d\boldsymbol{\omega} \tag{3.54}$

其中 $E(\boldsymbol{\omega})$ 可以看作是正则化的平方和误差函数，如果不考虑一些比例常数的话。通过对参数 $\omega$ 配平方，可以得到，

E (ω) = E (m N) + 1 2 (ω - m N) T A (ω - m N) (3.55)

$E(\boldsymbol{\omega}) = E(\boldsymbol{m}_N) + \frac{1}{2}(\boldsymbol{\omega}-\boldsymbol{m}_N)^T\textbf{A}(\boldsymbol{\omega}-\boldsymbol{m}_N) \tag{3.55}$

其中，

A = α I + β Φ T Φ E (m N) = β 2 | | t - Φ m N | | 2 + β 2 m T N m N m N = β A - 1 Φ T t (3.56) (3.57) (3.58)

$\begin{gather} \textbf{A} = \alpha \boldsymbol{I} + \beta \mathbf{\Phi}^T\mathbf{\Phi} \tag{3.56} \\ E(\boldsymbol{m}_N)=\frac{\beta}{2}||\textbf{t}-\mathbf{\Phi}\boldsymbol{m}_N||^2+\frac{\beta}{2}\boldsymbol{m}_N^T\boldsymbol{m}_N \tag{3.57} \\ \boldsymbol{m}_N = \beta \textbf{A}^{-1}\mathbf{\Phi}^T\textbf{t} \tag{3.58} \end{gather}$

对于式(3.54)的边缘似然函数，其对数形式定义为，

l n p (t | α, β) = M 2 l n α + N 2 l n β - E (m N) - 1 2 l n | A | - N 2 l n (2 π) (3.59)

$ln p(\textbf{t}|\alpha, \beta)=\frac{\boldsymbol{M}}{2}ln\alpha+\frac{\boldsymbol{N}}{2}ln\beta-E(\boldsymbol{m}_N)-\frac{1}{2}ln|\boldsymbol{A}|-\frac{N}{2}ln(2\pi) \tag{3.59}$

式(3.59)即为证据函数的表达式。

b. Maximizing the evidence function

最大化证据函数的主要目的式根据式(3.59)求出超参数 $\alpha$ 、 $\beta$ 的最佳近似 $\hat{\alpha}$ 、 $\hat{\beta}$ 。首先定义式(3.60)的特征向量方程，

(β Φ T Φ) μ i = λ i μ i (3.60)

$(\beta \mathbf{\Phi}^T\mathbf{\Phi})\boldsymbol{\mu}_i=\lambda_i \boldsymbol{\mu}_i \tag{3.60}$

由式(3.56)可知 $\textbf{A}$ 的特征值为 $\alpha+\lambda_i$ ，则对于式(3.59)中的 $ln|\mathbf{A}|$ 对于 $\alpha$ 求导，

d d α l n | A | = d d α l n \prod i (λ i + α) = d d α \sum i l n (λ i + α) = \sum i 1 λ i + α (3.61)

$\begin{aligned} \frac{d}{d\alpha}ln|\textbf{A}| &= \frac{d}{d\alpha} ln\prod_i (\lambda_i + \alpha) \\ &= \frac{d}{d\alpha} \sum_i ln(\lambda_i + \alpha) \\ &= \sum_i \frac{1}{\lambda_i+\alpha} \end{aligned} \tag{3.61}$

因此式(3.59)对 $\alpha$ 求偏导可得，

α = γ m T N m N γ = \sum i λ i α + λ i (3.62) (3.63)

$\begin{gather} \alpha = \frac{\gamma}{\boldsymbol{m}_N^T\boldsymbol{m}_N} \tag{3.62} \\ \gamma = \sum_i \frac{\lambda_i}{\alpha + \lambda_i} \tag{3.63} \end{gather}$

类似地，我们可以使式(3.59)对 $\beta$ 求偏导，进而得到，

1 β = 1 N - γ \sum n = 1 N {t n - m T N ϕ (x n)} 2 (3.64)

$\frac{1}{\beta} = \frac{1}{N-\gamma}\sum_{n=1}^N\{ t_n - \boldsymbol{m}_N^T\boldsymbol{\phi}(\boldsymbol{x}_n) \}^2 \tag{3.64}$

c. Effective number of parameters

式(3.62)定义了超参数 $\alpha$ 的值，这一值通过式(3.53)中的先验分布 $p(\boldsymbol{\omega}|\alpha)$ 控制着参数 $\boldsymbol{\omega}$ 的分布，考虑式(3.63)，显然有 $\frac{\lambda_i}{\lambda_i+\alpha}$ 位于0到1之间，因此式(3.63)中 $0 \leq \gamma \leq M$ 。对 $\alpha$ 的值的影响则主要分为两种情况，

情况一： $\lambda_i \gg \alpha$ ，此时 $\gamma$ 接近于1，因此对应的参数 $\omega_i$ 将会与最大似然值接近。
情况二： $\lambda_i \ll \alpha$ ，此时 $\gamma$ 接近于0，相对应的参数 $\omega_i$ 也会接近于0。

由于以上两种情况，我们可以利用 $\gamma$ 很好的度量先验分布 $p(\boldsymbol{\omega}|\alpha)$ 中的参数数量。

Code

https://github.com/zhoudinglive/PRML_exercise

zhoudinglive

关注

1
点赞
踩
1

收藏

觉得还不错? 一键收藏
0
评论
PRML Chapter 03 Linear Models for Regression

PRML Chapter 03 Linear Models for Regression本章主要介绍了监督学习中的基本模型——线性回归模型，即对给定的DDD维输入，输出一个或者多个连续的目标变量ttt，如第一章介绍的多项式拟合模型即是一种简单的线性回归模型。PRML Chapter 03 Linear Models for RegressionLinear Basis Funct...
复制链接

扫一扫