树形数据在关系数据库中的存储同对象一样,都会遇到一个"阻抗不匹配"的问题。如何设计一个表结构,才能较好的满足需求呢?
事实上,有很多解决方案,但是没有哪一种是放之四海而皆准的。我个人认为解决方案的选择,必须依赖于需求背景。抛弃需求背景而就技术泛泛而谈,就如同孔乙己对回字不同写法的孜孜追求,满身酸腐之气。
凡事有得就有失,十全十美的方案是不存的,合适的就是最好的。
下面就集中常见的方案做一下比对,然后详细分析一下第四种方案。
方案一:parent_id
Pros:
- 非常容易实现
- 很方便的将子树移动到另外一个节点
- 添加节点非常简单
Cons:
- 检索整棵树需要使用递归,非常耗费时间
- 查找指定节点的所有父(子)节点同样要使用递归,非常耗费时间
方案二: Path栏位
表添加Path栏位,每个节点记录从根节点到自身的一个路径。
Pros:
- 很容易查找所有父子节点
- 很容易检索整棵树
- 添加节点很简单
Cons:
- 移动子树比较麻烦,会导致大量数据更新
- 取决于path的存储方式,可能需要对path进行解析
方案三:Path表
建立一个表,记录节点和其所有父节点的关联关系。
Pros:
- 很容易查找所有父子节点
- 很容易检索整棵树
Cons:
- 添加节点很麻烦,需要同时产生很多关联关系
- 移动子树导致大量数据操作
- 数据量可能很庞大
方案四: 预排序遍历树算法(modified preorder tree traversal algorithm)
Pros:
- 很容易查找所有父子节点
- 很容易检索整棵树
- 直接使用SQL就可以得到相关的数据
- 存储方式决定了子节点都是有序存储的
Cons:
- 新增,更新,移动都很复杂,每次都会变更非常多的数据
第四种方案的算法的图例如下,这个图例比较难以理解,我另外做了个图例,以矩形嵌套来描述它。如下面的图一图二:

(图一)
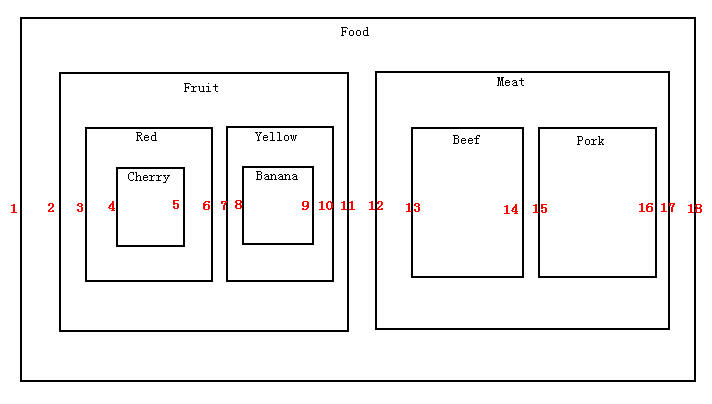
(图二)
图二中的节点以矩形嵌套矩形的方式来描述父子关系,每个框代表一个节点,左右边框各记录一个值。值的维护从左到右依次递增。
这个图例很容易看出如何使用一个节点的左右边界值来查找其子节点。
我们转成二维表,看看数据库的存储形式:
| Parent | Title | lft | rgt |
| Food | 1 | 18 | |
| Food | Fruit | 2 | 11 |
| Fruit | Red | 3 | 6 |
| Red | Cherry | 4 | 5 |
| Fruit | Yellow | 7 | 10 |
| Yellow | Banana | 8 | 9 |
| Food | Meat | 12 | 17 |
| Meat | Beef | 13 | 14 |
| Meat | Pork | 15 | 16 |
下面我们来看看树上的典型操作如何实现:
1. 检索树
给定一个节点,查找该节点及其子节点的sql:
SELECT * FROM tree WHERE lft BETWEEN 2 AND 11 ORDER BY lft ASC;2. 查找所有父节点
所有父节点的特征是左边值小于当前节点的左值,右边值大于当前节点的右值
SELECT title FROM tree WHERE lft < 4 AND rgt > 5 ORDER BY lft ASC;
3. 查找路径 Food > Cherry
select * from tree where lft between 1 and 4 and rgt between 5 and 18 order by lft
改变lft的排序方式,即可实现从父节点>子节点,或者子节点到父节点
每个子节点占2个数据,计算公式如下。判断当前节点是否叶子节点,或者有多少个子节点,可以根据下面的公式
descendants = (right - left - 1) / 2
5. 新增子节点
以在
Food>Fruit>Yellow 右边再增加一个新的兄弟节点Black为例子
1) 父节点的右边值为11. 新节点的左右值应该为 11, 12
2) 变更所有的受影响的节点,给新节点腾出空位子。
所有左节点>=11的,都增加2
6. 删除子节点
以删除 Food>Fruit>Red 节点为例子
update tree set lft = lft + 2 where lft>=11update tree set rgt = rgt + 2 where rgt>=11INSERT INTO tree SET lft=11, rgt=12, title='Black'以删除 Food>Fruit>Red 节点为例子
1) 删除子节点及其下面所有节点
delete from tree where lft >= 3 and rgt <= 6
2) 变更所有的受影响的节点.
所有左节点大于6的减去4 (rgt - lft + 1)
update tree set lft = lft - 4 where lft > 6
所有右节点大于6的减去4
update tree set rgt = rgt - 4 where rgt> 6
7. 移动子节点
以将
Food>Fruit>Yellow 移动到
Food>Meat>Pork下为例子:
要移动的节点是(7,11),目标节点是(15,16)
1) 以目标节点的Pork为参考,变更要移动节点的值
update tree set lft = lft + 9, rht=rgt + 9 where lft >=7 and rgt<=11
2) 原节点所在位置以被删除看待
所有左节点大于11的减去5 (rgt - lft + 1)
update tree set lft = lft - 5 where lft > 11
所有右节点大于11的减去5
update tree set rgt = rgt - 5 where rgt> 11
可以看出这种方法的最大优势是提升了读的性能,但是牺牲了写的性能,而且写的时候必须锁表。
以下资料供参考:






















 977
977

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








