1|随机信号分析与应用:从自相关到功率谱密度的探讨
目录
:::block-1
1. 随机信号的自相关函数及其应用
1.1 自相关函数的定义
1.2 自相关函数的性质
1.3 自相关函数的实际应用
:::
2. 随机信号的互相关函数及其应用
2.1 互相关函数的定义
2.2 互相关函数的性质
2.3 互相关函数在信号处理中的应用
3. 随机信号的功率谱估计
3.1 功率谱的概念
3.2 功率谱估计的基本方法
3.3 实例分析:功率谱估计在通信中的应用
4. 随机信号的功率谱密度
4.1 功率谱密度的定义
4.2 功率谱密度的物理意义
4.3 功率谱密度的计算方法
5. 功率谱密度的性质
5.1 功率谱密度的基本性质
5.2 功率谱密度的实际意义
5.3 功率谱密度与信号特征的关系
6. 功率谱密度与自相关函数的关系
6.1 Wiener-Khinchin定理
6.2 频域与时域的对应关系
6.3 实例分析:如何通过自相关函数获得功率谱密度
7. 功率谱估计的方法
7.1 基于自相关函数的功率谱估计
7.2 快速傅里叶变换(FFT)法
7.3 滑动窗法与周期图法
8. 功率谱估计的应用
8.1 在信号处理中的应用
8.2 在医学成像中的应用
8.3 在雷达信号分析中的应用
9. 互谱密度及其估计
9.1 互谱密度的定义
9.2 互谱密度估计方法
9.3 互谱密度在多通道信号分析中的应用
1. 随机信号的自相关函数及其应用
1.1 自相关函数的定义
我们日常接触到的信号,比如音频、温度、金融数据等,往往具有随机性。为了分析这些随机信号,我们需要一种工具来衡量信号在不同时间点上的相似性,这就是自相关函数。
假设你有一个信号 X ( t ) X(t) X(t),你可能会好奇:在不同时刻,这个信号的波动会有多相似?例如,地震信号在不同时间段的波动是否存在某种规律?在通信系统中,信号是否会因为多次反射和干扰而产生重复的模式?自相关函数就是用来回答这些问题的工具。
**自相关函数描述了同一个信号在不同时间滞后下的相似程度。**具体来说:
设 X ( t ) X(t) X(t) 是一个随机信号(信号的均值不一定为零),那么它的自相关函数 R X ( τ ) R_X(\tau) RX(τ) 表示信号在时刻 t t t 与滞后时间 τ \tau τ 之后的信号 X ( t + τ ) X(t + \tau) X(t+τ) 之间的相似性。形式化地,自相关函数定义为:
R X ( τ ) = lim T → ∞ 1 T ∫ − T / 2 T / 2 ( X ( t ) − E [ X ( t ) ] ) ( X ( t + τ ) − E [ X ( t + τ ) ] ) d t R_X(\tau) = \lim_{T \to \infty} \frac{1}{T} \int_{-T/2}^{T/2} \left(X(t) - E[X(t)]\right) \left(X(t+\tau) - E[X(t+\tau)]\right) \, dt RX(τ)=T→∞limT1∫−T/2T/2(X(t)−E[X(t)])(X(t+τ)−E[X(t+τ)])dt
其中:
- X ( t ) X(t) X(t) 是信号在时刻 t t t 的取值,
- E [ X ( t ) ] E[X(t)] E[X(t)] 表示信号 X ( t ) X(t) X(t) 的期望值,
- τ \tau τ 是滞后时间,表示信号在两个不同时间点之间的时间差。
动机:
- 先考虑信号 X ( t ) X(t) X(t) 在某一时刻 t t t 的取值。
- 接着考虑在此时刻滞后 τ \tau τ 时间之后,信号 X ( t + τ ) X(t + \tau) X(t+τ) 的取值。
- 自相关函数通过对 X ( t ) X(t) X(t) 与 X ( t + τ ) X(t + \tau) X(t+τ) 的乘积取积分并求期望,衡量这两个时刻的信号值有多相似。
这意味着,如果信号在时间 t t t 和 t + τ t + \tau t+τ 处的值较为相似,那么它们的乘积将是一个较大的正数,从而导致自相关函数在该滞后值 τ \tau τ 处取较大值。
1.2 自相关函数的性质
理解了定义后,我们来探讨自相关函数的几个关键性质。这些性质不仅是数学上的推导结果,也是实际应用中常见的特性。
1. 对称性
自相关函数在滞后时间 τ \tau τ 上具有对称性,即 R X ( τ ) = R X ( − τ ) R_X(\tau) = R_X(-\tau) RX(τ)=RX(−τ)。
证明:
我们从自相关函数的定义开始:
R X ( τ ) = lim T → ∞ 1 T ∫ − T / 2 T / 2 ( X ( t ) − E [ X ( t ) ] ) ( X ( t + τ ) − E [ X ( t + τ ) ] ) d t R_X(\tau) = \lim_{T \to \infty} \frac{1}{T} \int_{-T/2}^{T/2} \left(X(t) - E[X(t)]\right) \left(X(t+\tau) - E[X(t+\tau)]\right) \, dt RX(τ)=T→∞limT1∫−T/2T/2(X(t)−E[X(t)])(X(t+τ)−E[X(t+τ)])dt
为了证明 R X ( τ ) = R X ( − τ ) R_X(\tau) = R_X(-\tau) RX(τ)=RX(−τ),我们可以进行变量替换。设 u = t + τ u = t + \tau u=t+τ,因此 d u = d t du = dt du=dt,积分上下限相应变为 − T / 2 + τ -T/2 + \tau −T/2+τ 到 T / 2 + τ T/2 + \tau T/2+τ。原积分式变为:
R X ( τ ) = lim T → ∞ 1 T ∫ − T / 2 + τ T / 2 + τ ( X ( u − τ ) − E [ X ( u − τ ) ] ) ( X ( u ) − E [ X ( u ) ] ) d u R_X(\tau) = \lim_{T \to \infty} \frac{1}{T} \int_{-T/2+\tau}^{T/2+\tau} \left(X(u-\tau) - E[X(u-\tau)]\right) \left(X(u) - E[X(u)]\right) \, du RX(τ)=T→∞limT1∫−T/2+τT/2+τ(X(u−τ)−E[X(u−τ)])(X(u)−E[X(u)])du
由于积分的时间跨度趋近于无穷大,可以将积分上下限重新变换回原来的形式,即:
R X ( τ ) = lim T → ∞ 1 T ∫ − T / 2 T / 2 ( X ( t ) − E [ X ( t ) ] ) ( X ( t − τ ) − E [ X ( t − τ ) ] ) d t R_X(\tau) = \lim_{T \to \infty} \frac{1}{T} \int_{-T/2}^{T/2} \left(X(t) - E[X(t)]\right) \left(X(t-\tau) - E[X(t-\tau)]\right) \, dt RX(τ)=T→∞limT1∫−T/2T/2(X(t)−E[X(t)])(X(t−τ)−E[X(t−τ)])dt
这个表达式与 R X ( − τ ) R_X(-\tau) RX(−τ) 的定义一致,因此:
R X ( τ ) = R X ( − τ ) R_X(\tau) = R_X(-\tau) RX(τ)=RX(−τ)
这证明了自相关函数是对称的,即 R X ( τ ) = R X ( − τ ) R_X(\tau) = R_X(-\tau) RX(τ)=RX(−τ)。
2. 非负性与最大值
自相关函数在 τ = 0 \tau = 0 τ=0 时达到最大值,即 R X ( 0 ) R_X(0) RX(0) 是最大值且非负。
证明:
当 τ = 0 \tau = 0 τ=0 时,自相关函数的表达式为:
R X ( 0 ) = lim T → ∞ 1 T ∫ − T / 2 T / 2 ( X ( t ) − E [ X ( t ) ] ) 2 d t R_X(0) = \lim_{T \to \infty} \frac{1}{T} \int_{-T/2}^{T/2} \left(X(t) - E[X(t)]\right)^2 \, dt RX(0)=T→∞limT1∫−T/2T/2(X(t)−E[X(t)])2dt
这个公式表示信号 X ( t ) X(t) X(t) 的方差 σ X 2 \sigma_X^2 σX2,即:
σ X 2 = E [ ( X ( t ) − E [ X ( t ) ] ) 2 ] = lim T → ∞ 1 T ∫ − T / 2 T / 2 ( X ( t ) − E [ X ( t ) ] ) 2 d t \sigma_X^2 = E\left[\left(X(t) - E[X(t)]\right)^2\right] = \lim_{T \to \infty} \frac{1}{T} \int_{-T/2}^{T/2} \left(X(t) - E[X(t)]\right)^2 dt σX2=E[(X(t)−E[X(t)])2]=T→∞limT1∫−T/2T/2(X(t)−E[X(t)])2dt
由于方差总是非负的,即 σ X 2 ≥ 0 \sigma_X^2 \geq 0 σX2≥0,所以有:
R X ( 0 ) = σ X 2 ≥ 0 R_X(0) = \sigma_X^2 \geq 0 RX(0)=σX2≥0
最大值的解释:
当 τ = 0 \tau = 0 τ=0 时,信号与自身完全重合,因此自相关函数的值为信号的方差 σ X 2 \sigma_X^2 σX2,即:
R X ( 0 ) = σ X 2 R_X(0) = \sigma_X^2 RX(0)=σX2
对于任意 τ ≠ 0 \tau \neq 0 τ=0,由于信号在不同时刻之间的相关性通常减弱, R X ( τ ) R_X(\tau) RX(τ) 通常小于或等于 R X ( 0 ) R_X(0) RX(0)。这意味着 R X ( 0 ) R_X(0) RX(0) 是自相关函数的全局最大值。这是因为随着滞后时间的增加,信号在两个时刻之间的相关性逐渐降低,自相关函数的值也随之减小。
3. 正定性
自相关函数具有正定性,这意味着对于任意的非零实数 a 1 , a 2 , … , a n a_1, a_2, \ldots, a_n a1,a2,…,an 和时间点 t 1 , t 2 , … , t n t_1, t_2, \ldots, t_n t1,t2,…,tn,满足:
∑ i = 1 n ∑ j = 1 n a i a j R X ( t i − t j ) ≥ 0 \sum_{i=1}^{n} \sum_{j=1}^{n} a_i a_j R_X(t_i - t_j) \geq 0 i=1∑nj=1∑naiajRX(ti−tj)≥0
证明:
正定性性质表示,对于任意实数 a 1 , a 2 , … , a n a_1, a_2, \ldots, a_n a1,a2,…,an 和时间点 t 1 , t 2 , … , t n t_1, t_2, \ldots, t_n t1,t2,…,tn,有:
∑ i = 1 n ∑ j = 1 n a i a j R X ( t i − t j ) ≥ 0 \sum_{i=1}^{n} \sum_{j=1}^{n} a_i a_j R_X(t_i - t_j) \geq 0 i=1∑nj=1∑naiajRX(ti−tj)≥0
我们可以将上式展开,并看作信号的一个线性组合的自相关函数之和。设 Y ( t ) Y(t) Y(t) 为信号 X ( t ) X(t) X(t) 的线性组合:
Y ( t ) = ∑ i = 1 n a i X ( t + t i ) Y(t) = \sum_{i=1}^{n} a_i X(t + t_i) Y(t)=i=1∑naiX(t+ti)
需要计算 Y ( t ) Y(t) Y(t) 的方差 Var ( Y ( t ) ) \text{Var}(Y(t)) Var(Y(t))。根据方差的定义, Var ( Y ( t ) ) \text{Var}(Y(t)) Var(Y(t)) 为:
Var ( Y ( t ) ) = E [ Y ( t ) 2 ] = E [ ( ∑ i = 1 n a i X ( t + t i ) ) 2 ] \text{Var}(Y(t)) = E[Y(t)^2] = E\left[\left(\sum_{i=1}^{n} a_i X(t + t_i)\right)^2\right] Var(Y(t))=E[Y(t)2]=E (i=1∑naiX(t+ti))2
将上式展开:
Var ( Y ( t ) ) = E [ ∑ i = 1 n ∑ j = 1 n a i a j X ( t + t i ) X ( t + t j ) ] \text{Var}(Y(t)) = E\left[\sum_{i=1}^{n} \sum_{j=1}^{n} a_i a_j X(t + t_i) X(t + t_j)\right] Var(Y(t))=E[i=1∑nj=1∑naiajX(t+ti)X(t+tj)]
利用自相关函数的定义,上式可以重写为:
Var ( Y ( t ) ) = ∑ i = 1 n ∑ j = 1 n a i a j E [ X ( t + t i ) X ( t + t j ) ] = ∑ i = 1 n ∑ j = 1 n a i a j R X ( t i − t j ) \text{Var}(Y(t)) = \sum_{i=1}^{n} \sum_{j=1}^{n} a_i a_j E\left[X(t + t_i) X(t + t_j)\right] = \sum_{i=1}^{n} \sum_{j=1}^{n} a_i a_j R_X(t_i - t_j) Var(Y(t))=i=1∑nj=1∑naiajE[X(t+ti)X(t+tj)]=i=1∑nj=1∑naiajRX(ti−tj)
因为方差 Var ( Y ( t ) ) \text{Var}(Y(t)) Var(Y(t)) 总是非负的,即 Var ( Y ( t ) ) ≥ 0 \text{Var}(Y(t)) \geq 0 Var(Y(t))≥0,因此有:
∑ i = 1 n ∑ j = 1 n a i a j R X ( t i − t j ) ≥ 0 \sum_{i=1}^{n} \sum_{j=1}^{n} a_i a_j R_X(t_i - t_j) \geq 0 i=1∑nj=1∑naiajRX(ti−tj)≥0
这就证明了自相关函数的正定性性质。方差总是非负的这一事实源于数学中的基本定理,因此所有的自相关函数都具有正定性。
1.3 自相关函数的实际应用
接下来我将通过多图对比的方式进行展示,直观地看到信号的不同特性。
应用一:信号的周期性检测
检测信号的周期性是自相关函数的一个重要应用。通过生成一个正弦波信号,并计算其自相关函数,来观察其周期性特征。然后再与一个非周期性信号的自相关函数进行对比。
Matlab实现:
首先生成一个周期性的正弦波信号,以及一个随机噪声信号,并分别计算它们的自相关函数。
clc
clear
close all
f0 = 5;
T = 1;
Fs = 1000;
t = 0:1/Fs:T;
X_sin = sin(2*pi*f0*t);
X_rand = randn(size(t));
[acf_sin, lags_sin] = xcorr(X_sin, 'coeff');
[acf_rand, lags_rand] = xcorr(X_rand, 'coeff');
figure;
subplot(2,1,1);
plot(lags_sin/Fs, acf_sin);
title('正弦波信号的自相关函数');
xlabel('滞后时间 (秒)');
ylabel('自相关系数');
grid on;
subplot(2,1,2);
plot(lags_rand/Fs, acf_rand);
title('随机信号的自相关函数');
xlabel('滞后时间 (秒)');
ylabel('自相关系数');
grid on;
代码说明:
f0 = 5设置了正弦波的频率为5Hz,即每秒钟信号会完成5个周期。T = 1表示信号的持续时间为1秒。Fs = 1000设定了采样频率为1000Hz,这意味着每秒采集1000个样本。xcorr函数用于计算信号的自相关函数。'coeff'参数标准化了自相关函数的结果,使得自相关系数的取值范围在 [-1, 1] 之间,便于对不同信号的自相关性进行对比。
实验结果:
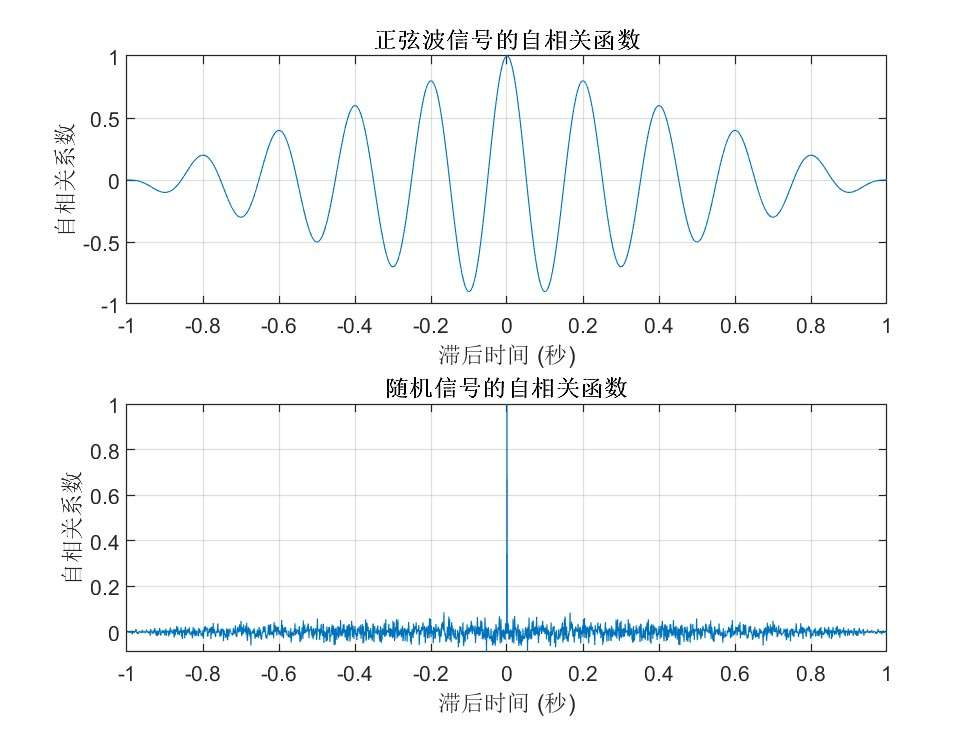
- 正弦波信号的自相关函数:自相关函数在滞后时间为信号周期的整数倍时出现明显的峰值。这表明正弦波信号具有周期性,并且自相关函数可以清楚地反映这一特性。
- 随机信号的自相关函数:与正弦波信号不同,随机信号的自相关函数在滞后时间 τ ≠ 0 \tau \neq 0 τ=0 时几乎没有显著的相关性,这反映了随机信号的无周期性特征。
应用二:信号噪声分离
自相关函数还可以用于区分信号与噪声。在实际应用中,信号常常伴随噪声。通过计算总信号的自相关函数,我们是可以区分其中的信号成分和噪声成分。
Matlab实现:
生成一个正弦波信号,并叠加随机噪声,计算总信号和纯噪声的自相关函数,以进行对比。
clc
clear
close all
f0 = 5;
T = 1;
Fs = 1000;
t = 0:1/Fs:T;
X_sin = sin(2*pi*f0*t);
N = randn(size(t));
Y = X_sin + N;
[acf_Y, lags_Y] = xcorr(Y, 'coeff');
[acf_N, lags_N] = xcorr(N, 'coeff');
figure;
subplot(2,1,1);
plot(lags_Y/Fs, acf_Y);
title('总信号 (正弦波 + 噪声) 的自相关函数');
xlabel('滞后时间 (秒)');
ylabel('自相关系数');
grid on;
subplot(2,1,2);
plot(lags_N/Fs, acf_N);
title('纯噪声信号的自相关函数');
xlabel('滞后时间 (秒)');
ylabel('自相关系数');
grid on;
代码说明:
- 在总信号 Y Y Y 中,正弦波信号和随机噪声信号被叠加在一起。这种情况下,虽然存在噪声,自相关函数仍然可以识别出正弦波的周期性。
- 纯噪声信号的自相关函数通常在 τ ≠ 0 \tau \neq 0 τ=0 时几乎为零,表示噪声信号在不同时刻之间没有相关性。
实验结果:
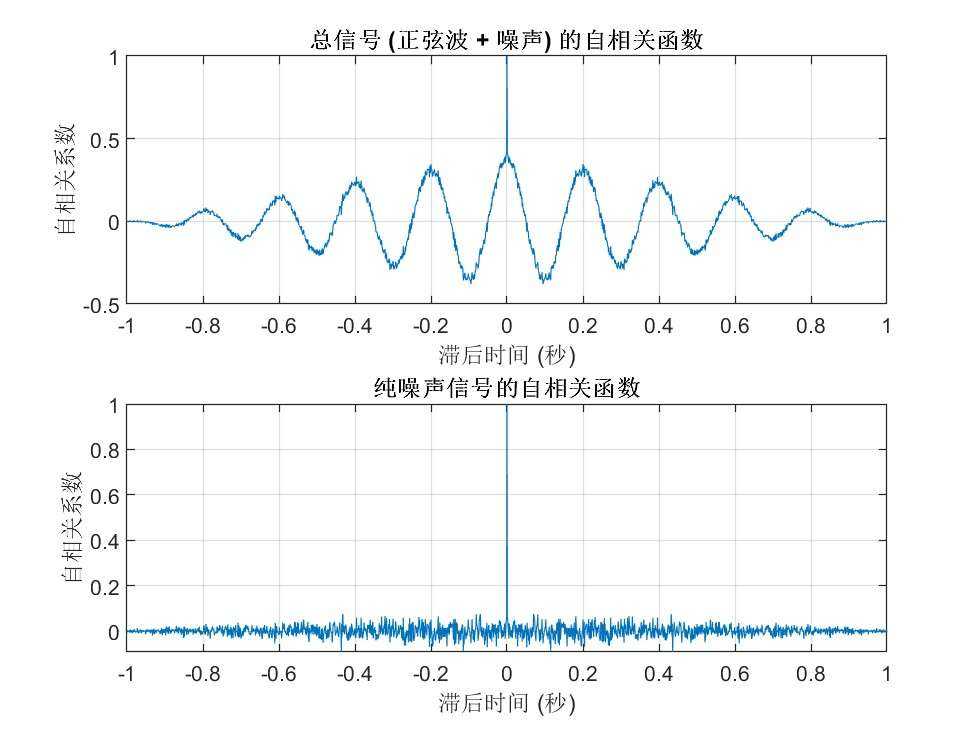
- 总信号的自相关函数:虽然总信号中包含噪声,但由于信号的周期性,自相关函数仍然在周期倍数的滞后时间处显示出峰值。这表明自相关函数能够揭示总信号中的周期性成分,即使在噪声存在的情况下。
- 纯噪声的自相关函数:纯噪声信号的自相关函数在 τ ≠ 0 \tau \neq 0 τ=0 时几乎为零,说明噪声信号在不同时刻之间没有相关性。这一特性也体现了噪声的随机性。
小结
自相关函数是分析随机信号的重要工具,通过衡量信号在不同时刻的相似性,自相关函数能够揭示信号的周期性、相关性等特征。本文主要探讨了自相关函数的定义和基本性质,并结合MATLAB展示了自相关函数在信号处理中的重要性。
另外,对自相关函数的对称性、非负性与最大值、正定性等性质进行证明。
通过对比实验结果,本文展示了自相关函数在周期性检测和信号噪声分离中的应用。
微信公众号:JIAFEIMAO的摆烂日常






















 3978
3978

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








