第十三周项目4-Floyd算法验证

问题：

[cpp]  view plain  copy

 

1. /*  
2. * Copyright (c)2016,烟台大学计算机与控制工程学院  
3. * All rights reserved.  
4. * 文件名称：项目4.cbp  
5. * 作    者：陈晓琳  
6. * 完成日期：2016年11月24日  
7. * 版 本 号：v1.0  
8.   
9. * 问题描述：Floyd算法的验证  
10.   
11. * 输入描述：无  
12. * 程序输出：测试数据  
13. */    

头文件及功能函数见【图算法库】

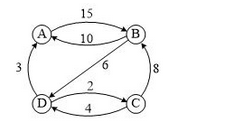
测试用图：

代码：

[cpp]  view plain  copy

 

1. #include "graph.h"    
2. #define MaxSize 100    
3.     
4. void Ppath(int path[][MAXV],int i,int j)  //前向递归查找路径上的顶点    
5. {    
6.     int k;    
7.     k=path[i][j];    
8.     if (k==-1) return;  //找到了起点则返回    
9.     Ppath(path,i,k);    //找顶点i的前一个顶点k    
10.     printf("%d,",k);    
11.     Ppath(path,k,j);    //找顶点k的前一个顶点j    
12. }    
13. void Dispath(int A[][MAXV],int path[][MAXV],int n)    
14. {    
15.     int i,j;    
16.     for (i=0; i<n; i++)    
17.         for (j=0; j<n; j++)    
18.         {    
19.             if (A[i][j]==INF)    
20.             {    
21.                 if (i!=j)    
22.                     printf("从%d到%d没有路径\n",i,j);    
23.             }    
24.             else    
25.             {    
26.                 printf("  从%d到%d=>路径长度:%d 路径:",i,j,A[i][j]);    
27.                 printf("%d,",i);    //输出路径上的起点    
28.                 Ppath(path,i,j);    //输出路径上的中间点    
29.                 printf("%d\n",j);   //输出路径上的终点    
30.             }    
31.         }    
32. }    
33. void Floyd(MGraph g)    
34. {    
35.     int A[MAXV][MAXV],path[MAXV][MAXV];    
36.     int i,j,k;    
37.     for (i=0; i<g.n; i++)    
38.         for (j=0; j<g.n; j++)    
39.         {    
40.             A[i][j]=g.edges[i][j];    
41.             path[i][j]=-1;    
42.         }    
43.     for (k=0; k<g.n; k++)    
44.     {    
45.         for (i=0; i<g.n; i++)    
46.             for (j=0; j<g.n; j++)    
47.                 if (A[i][j]>A[i][k]+A[k][j])    
48.                 {    
49.                     A[i][j]=A[i][k]+A[k][j];    
50.                     path[i][j]=k;    
51.                 }    
52.     }    
53.     Dispath(A,path,g.n);   //输出最短路径    
54. }    
55. int main()    
56. {    
57.     MGraph g;    
58.     int A[4][4]=    
59.     {    
60.         {0,  15,INF,INF},    
61.         {10,  0,INF,  6},    
62.         {INF, 8,  0,  2},    
63.         {3,  INF, 2,  0}    
64.     };    
65.     ArrayToMat(A[0], 4, g);    
66.     Floyd(g);    
67.     return 0;    
68. }    

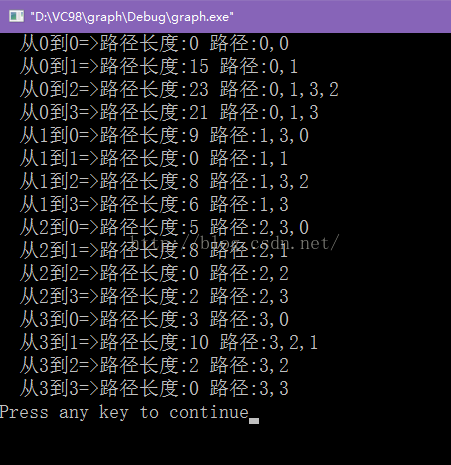
运行结果：

知识点总结：

Floyd算法的验证。