3200. 三角形的最大高度

3200. 三角形的最大高度

简单

给你两个整数 red 和 blue，分别表示红色球和蓝色球的数量。你需要使用这些球来组成一个三角形，满足第 1 行有 1 个球，第 2 行有 2 个球，第 3 行有 3 个球，依此类推。

每一行的球必须是 相同 颜色，且相邻行的颜色必须 不同。

返回可以实现的三角形的 最大 高度。

示例 1：

输入： red = 2, blue = 4

输出： 3

解释：

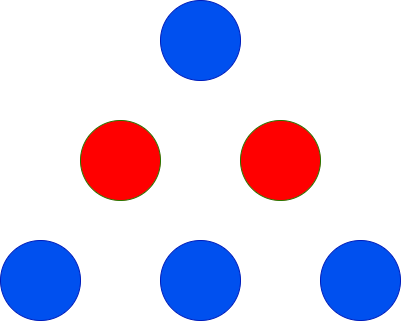
上图显示了唯一可能的排列方式。

示例 2：

输入： red = 2, blue = 1

输出： 2

解释：

[外链图片转存中…(img-2ZTxed3r-1729001870986)]
上图显示了唯一可能的排列方式。

示例 3：

输入： red = 1, blue = 1

输出： 1

示例 4：

输入： red = 10, blue = 1

输出： 2

解释：

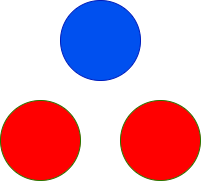
上图显示了唯一可能的排列方式。

提示：

• 1 <= red, blue <= 100

代码

class Solution {
public:
    int maxHeightOfTriangle(int red, int blue) {
        
        return max(redBottom(red, blue), blueBottom(red, blue));


    }
    int redBottom(int red,int blue)
    {
        int maxHeight=0;
        for(int i=1;;i++)
        {
            if(i%2==1)
            {
                red-=i;
                if(red<0)break;
                else maxHeight+=1;
            }
            else
            {
                blue-=i;
                if(blue<0)break;
                else maxHeight+=1;
            }
        }
        return maxHeight;
    }
    int blueBottom(int red,int blue)
    {
        int maxHeight=0;
        for(int i=1;;i++)
        {
            if(i%2==0)
            {
                red-=i;
                if(red<0)break;
                else maxHeight+=1;
            }
            else
            {
                blue-=i;
                if(blue<0)break;
                else maxHeight+=1;
            }
        }
        return maxHeight;
    }
};

​ 直接对两种情况分别写两个对应的函数，直接返回其中的最大值。

优化代码

class Solution {
public:
    int maxHeightOfTriangle(int red, int blue) {
        return max(caculataMaxHeight(red, blue, 1), caculataMaxHeight(red, blue, 0));
    }
    int caculataMaxHeight(int red, int blue, bool isRedBottom)
    {
        int maxHeight=0;
        for(int i=1;;i++)
        {
            if(i%2==1&&isRedBottom||i%2==0&&!isRedBottom)
            {
                red-=i;
                if(red<0)break;
            }
            else
            {
                blue-=i;
                if(blue<0)break;
            }
            maxHeight+=1;
        }
        return maxHeight;
    }
};

​ 由于之前的两个函数代码逻辑相同，所以可以合并到同一个函数之中，通过添加布尔变量isRedBottom来区分两种情况，简化了代码。