大数据-贝叶斯算法

贝叶斯算法

​ 贝叶斯定理是概率论中的一个定理，描述在已知一些条件下，某事件的发生概率。比如，如果已知某种健康问题与寿命有关，使用贝叶斯定理则可以通过得知某人年龄，来更加准确地计算出默认有某种健康问题地概率。基本思想是：当不能准确知悉一个事物的本质时，可以依靠与事物特定本质相关事件出现的多少去判断其本质属性的概率，即支持某项属性的事件发生的越多，则该属性成立的可能性就越大。

因为贝叶斯模型是基于古典概型演算而来的，所以想要完全理解贝叶斯算法，我们需要从古典概率入手，来推演整个分类计算过程。

一、贝叶斯定理

1. 引入-概率题

小明有一次抽奖机会，他可以随机从三个箱子中抽奖，每个箱子中奖品数量都不一致，抽到红色小球为中奖。

1. 小明的中奖概率是多少？

2. 当小明已经中奖时，他是从二号箱子抽奖的概率是多少？
   
   从上图可以看出，他有50%的可能抽中一号箱、30%的可能抽中二号箱、20%的可能抽中三号箱。三个箱子的中奖率分别为10%、30%、20%。

第一个问题很简单，小明中奖的概率也就是三个中奖率之和，0.5*0.1+0.3*0.3+0.2*0.4=0.22 也就是22%的中奖率。

第二个问题会复杂一点，不是”由因到果“，而是已经中奖了，算从三号箱抽奖的概率，”从果推因“。这个概率会是30%*30%吗，很显然不是的，因为前提已经变了，前提是已经中奖，也就是说上面的22%是已经发生了的，这22%的中奖率是由三个箱子每个箱子的中奖率加上来的，总共也只有三个箱子能抽奖。那么这时小明已经中奖时，他从三号箱子抽奖的概率是不是就是第三号箱的中奖率占总中奖率的多少？
$$P(二号箱抽奖|中奖)=\frac{P(从二号箱抽奖的中奖)}{P(总的中奖)}=\frac{0.3\ast 0.3}{0.22}=\frac{9}{22}\approx 0.409$$
得出答案：当小明已经中奖时，他是从三号箱子抽奖的概率是40.9%。

第一题是从前往后推，第二题是已知结果从后往前推。因果顺序反转。

2. 贝叶斯公式

现在我们对上面的概率题分析一下，完成整个抽奖动作需要两步，第一步选中一个箱子，第二步从选中箱子中抽一个球。扩展一下的话我们还会有n个箱子。例如下图

如图，是一个两步式模型，首先第一步我们先完成事件A，有n种不同的路径，分别是从$A_1$到$A_n$。首先我们选择第一条路径走，第一步发生$A_1$的概率记为$P(A_1)$，然后在完成第一步后完成第二步，也就是在$A_1$的概率下完成$B$,这一段路径的概率记为$P(B|A_1)$。那么第一条路径整条路径的概率为$P(A_1)P(B|A_1)$。

比如上面的案例第一个抽奖箱是普惠性质的，我们有50%的概率在这个抽奖箱抽奖，但是这个抽奖箱的中奖概率只有10%。$P(A_1)=0.5$,$P(B|A_1)=0.1$ 那么我们在第一个抽奖箱中奖的概率就是$P(A_1)P(B|A_1)=0.5\ast 0.1=0.05$，那么同时还有其他的抽奖箱也是同样的，比如我们在第n个抽奖箱中奖的概率表示就是$P(A_n)P(B|A_n)$。

那么现在我们可以计算出我们能抽到奖品的概率就是每一条路径的概率相加，得到如下公式
$$P(B)=P(B{A}_1)+P(B{A}_2)+...+P(B{A}_n)=P(B|A_1)P(A_1)+P(B|A_2)P(A_2)+...+P(B|A_n)P(A_n)$$
那么这个公式也叫做全概率公式，$P(B)$也是$B$的先验概率。也就是把所有路径的概率之和加起来等于最终的概率。这也是“由因到果”。

全概率公式定理：

设试验$E$的样本空间为$S$，$B$为 $E$ 的事件，$A1,A2,\dots ,An$ 为$S$的一个划分，且 $P(A_i)>0(i=1,2,...,n)$，则
$$P(B)=P(B{A}_1)+P(B{A}_2)+...+P(B{A}_n)=P(B|A_1)P(A_1)+P(B|A_2)P(A_2)+...+P(B|A_n)P(A_n)$$

现在如果我们已经中奖了，不知道抽的几号箱，求已经中奖的前提下，是从二号抽奖箱抽中的概率。也就是求$P(A_2|B)$，从上面案例我们能轻松的推导出下面的公式
$$P(A_2|B)=\frac{P(2)}{P(1)+P(2)+...+P(n)}=\frac{P(A_2)\ast P(B|A_2)}{P(B|A_1)P(A_1)+P(B|A_2)P(A_2)+...+P(B|A_n)P(A_n)}=\frac{P(A_2)\ast P(B|A_2)}{P(B)}$$
于是乎我们就得到了贝叶斯公式：
$$P(A|B)=\frac{P(B|A)\ast P(A)}{P(B)}$$

公式中$P(A)$和$P(B)$一般称之为先验概率，一般是可以根据样本统计得来（在数据量很大的时候，根据中心极限定理，频率是等于概率）。$P(B|A)$是条件概率，$P(A|B)$是后验概率。

简单来说，贝叶斯定理（Bayes Theorem，也称贝叶斯公式）是基于假设的先验概率、给定假设下观察到不同数据的概率，提供了一种计算后验概率的方法。在人工智能领域，有一些

概率型模型会依托于贝叶斯定理。

贝叶斯公式定理：

设 $A_1,A_2,...,A_n$ 是样本空间的一个分割 (其中暗含了 $P(A_i)>0$)，$B$ 是 $\Omega$ 中的 一个事件，且 $P(B)>0$，那么
$$P(A_i|B)=\frac{P(A_{i}B)}{P(B)}=\frac{P(B|A_i)P(A_i)}{P(B)}=\frac{P(B|A_i)P(A_i)}{{\sum }_{j=0}^{n}P(B|A_j)P(A_j)}$$

上面使用的推导方式为比较容易理解的推导方式，看不懂可以使用文氏图推导再试一次。

二、朴素贝叶斯模型

1. 引入-概率题

我们推导出公式后，开始来个小案例运用一下。

如果一对男女朋友，男生想女生求婚，男生的四个特点分别是不帅，性格不好，身高矮，上进，请你根据下面的数据判断一下女生是嫁还是不嫁？

帅不帅	性格好不好	身高高不高	上进不上进	嫁不嫁
帅	不好	矮	不上进	不嫁
不帅	好	矮	上进	不嫁
帅	好	矮	上进	嫁
不帅	好	高	上进	嫁
帅	不好	矮	上进	不嫁
帅	不好	矮	上进	不嫁
帅	好	高	不上进	嫁
不帅	好	中	上进	嫁
帅	好	中	上进	嫁
不帅	不好	高	上进	嫁
帅	好	矮	不上进	不嫁
帅	好	矮	不上进	不嫁

这其实就是一个典型的分类问题，是一个二分类。根据四个特征来推算他的分类。也就是根据四个特征推算出“是嫁还是不嫁”。

帅不帅	性格好不好	身高高不高	上进不上进	嫁不嫁
不帅	性格不好	矮	上进	？

转为数学问题也就是比较$P(嫁|不帅、性格不好、身高矮、上进)$和$P(不嫁|不帅、性格不好、身高矮、上进)$的概率，谁的概率大，那就能给出嫁或不嫁的结论。

那么我们先计算$P(嫁|不帅、性格不好、身高矮、上进)$带入贝叶斯公式：
$$P(嫁|不帅、性格不好、身高矮、上进)=\frac{P(嫁)P(不帅、性格不好、身高矮、上进|嫁)}{P(不帅、性格不好、身高矮、上进)}$$
现在我们需要求得三个变量的值：$P(嫁)$、$P(不帅、性格不好、身高矮、上进|嫁)$、$P(不帅、性格不好、身高矮、上进)$

大样本下频率近似等于概率（大数定律），对与$P(嫁)$我们可以直接从样本统计：$P(嫁)=1/2$。

麻烦的是求$P(不帅、性格不好、身高矮、上进|嫁)$和$P(不帅、性格不好、身高矮、上进)$。可以从当前的数据样本中看出，没有同时符合这四个条件的数据，没有前人给我们直接的参考。如果我们想从现有的四个特征来求解的话，也会变得非常棘手，因为如果这四个特征之间相互有干扰，比如身高高会影响你帅不帅，我们要考虑干扰因素的话就非常难求解。特征值少的话可以勉强算一算，如果特征值一多，复杂度是次方级的增加，几乎无解。

为了方便我们计算，这个时候我们就要引入一个关键的假设：假设在类确定的条件下特征之间相互独立。

也就是上面四个特征不会相互影响，帅不帅不会影响性格等。这样我们就可以把公式转换成如下，这样就能求出来了。
$$P(不帅、性格不好、身高矮、上进|嫁)=P(不帅|嫁)P(性格不好|嫁)P(身高矮|嫁)P(上进|嫁)$$

事件的独立性：若 $A$, $B$ 独立，则 $P(AB)=P(A)P(B)$（不理解可以画坐概率标系理解）

最终‘嫁不嫁’公式就会变为如下：
$$P(嫁|不帅、性格不好、身高矮、上进)=\frac{P(嫁)P(不帅|嫁)P(性格不好|嫁)P(身高矮|嫁)P(上进|嫁)}{P(不帅)P(性格不好)P(身高矮)P(上进)}$$

‘不嫁’的公式：
$$P(不嫁|不帅、性格不好、身高矮、上进)=\frac{P(不嫁)P(不帅|不嫁)P(性格不好|不嫁)P(身高矮|不嫁)P(上进|不嫁)}{P(不帅)P(性格不好)P(身高矮)P(上进)}$$
现在我们就开始统计计算

$P(嫁)=\frac{1}{2}$

$P(不帅|嫁)=\frac{1}{2}$

$P(性格不好|嫁)=\frac{1}{6}$

$P(身高矮|嫁)=\frac{1}{6}$

$P(上进|嫁)=\frac{5}{6}$

$P(不嫁)=\frac{1}{2}$

$P(不帅|不嫁)=\frac{1}{6}$

$P(性格不好|不嫁)=\frac{1}{2}$

$P(身高矮|不嫁)=1$

$P(上进|不嫁)=\frac{1}{2}$

将概率代入公式：
$$P(嫁|不帅、性格不好、身高矮、上进)=\frac{\frac{1}{2}\ast \frac{1}{2}\ast \frac{1}{6}\ast \frac{1}{6}\ast \frac{5}{6}}{P(不帅)P(性格不好)P(身高矮)P(上进)}$$

$$P(不嫁|不帅、性格不好、身高矮、上进)=\frac{\frac{1}{2}\ast \frac{1}{6}\ast \frac{1}{2}\ast 1\ast \frac{1}{2}}{P(不帅)P(性格不好)P(身高矮)P(上进)}$$

两式分母相同，我们只比较分子就行。很显然$\frac{1}{2}\ast \frac{1}{2}\ast \frac{1}{6}\ast \frac{1}{6}\ast \frac{5}{6}<\frac{1}{2}\ast \frac{1}{6}\ast \frac{1}{2}\ast 1\ast \frac{1}{2}$。于是有$P(不嫁|不帅、性格不好、身高矮、上进)>P(嫁|不帅、性格不好、身高矮、上进)$。所以我们得到的结论就是女生不嫁。

这里的案例，把类似「帅不帅」这样的特征概率化，构成一个「女生好感度向量」以及对应的「嫁/不嫁标签」，训练出一个标准的「基于统计概率的嫁不嫁模型」，这些模型都是各个特征概率构成的。这个就是朴素贝叶斯模型。

2. 朴素贝叶斯算法

朴素贝叶斯（Naive Bayes）分类是贝叶斯分类中最简单，也是常见的一种分类方法。朴素贝叶斯算法的核心思想是通过考虑特征概率来预测分类，即对于给出的待分类样本，求解在此样本出现的条件下各个类别出现的概率，哪个最大，就认为此待分类样本属于哪个类别。

它的基本数学思想是：

对于给定的待分类项 X { a 1 , a 2 , a 3 , . . . , a n } X\{a_1,a_2,a_3,...,a_n\} X{a1​,a2​,a3​,...,an​}，求解在此项出现的条件下各个类别$y_i$出现的概率。哪个$P(y_i|X)$最大，就把此待分类项归属于哪个类别。

朴素贝叶斯算法定义为：

设 X { a 1 , a 2 , a 3 , . . . , a n } X\{a_1,a_2,a_3,...,a_n\} X{a1​,a2​,a3​,...,an​}为一个待分类项，每个$a_i$为$x$的一个特征属性，且特征属性之间相互独立。设 C { y 1 , y 1 , y 1 , . . . , y n } C\{y_1,y_1,y_1,...,y_n\} C{y1​,y1​,y1​,...,yn​}为一个类别集合，计算

$$P(y_1|X),P(y_2|X),P(y_3|X),...,P(y_n|X)$$

P ( y k ∣ X ) = m a x { P ( y 1 ∣ X ) , P ( y 2 ∣ X ) , P ( y 3 ∣ X ) . . . , P ( y n ∣ X ) } , 则 X ∈ y k P(y_k|X)=max\{P(y_1|X),P(y_2|X),P(y_3|X)...,P(y_n|X)\},则X\in y_k P(yk​∣X)=max{P(y1​∣X),P(y2​∣X),P(y3​∣X)...,P(yn​∣X)},则X∈yk​
带入贝叶斯公式推导：
$$P(y_i|X)=\frac{P(X|y_i)P(y_i)}{P(X)}$$
只求分子，因为各特征值是独立的所以有：
$$P(X|y_i)P(y_i)=P(a_1|y_i)P(a_2|y_i)...P(a_n|y_i)P(y_i)=P(y_i)\prod _{j=1}^{n}P(a_j|y_j)$$
对于先验概率 $P(a_j|y_j)$，是指在类别 $y_i$中，特征元素$a_j$出现的概率，可以求解为：
$$P(a_j|y_i)=\frac{|在训练样本为y_i时，a_j出现的次数|}{|y_i训练样本数|}$$

其中朴素，是假定所有输入事件之间是相互独立。进行这个假设是因为独立事件间的概率计算更简单。但同时也会牺牲一定的分类准确率。

为何一定要事件独立，上面有提到过。

1. 如果特征条件不相互独立，我们需要考虑各特征条件的干扰。随着特征个数增加，复杂度是次方级的增加。
2. 由于数据的稀疏性，同时满足多特征的数据通常统计不到。

朴素贝叶斯算法应用场景：文本分类、垃圾邮件识别、情感预测

优点：

• 数据量少，计算简单。所以易实现、开销小。
• 对小规模数据表现好，对缺失数据不太敏感。
• 分类效率稳定。

缺点：

• 属性之间相互独立，这个假设在实际应用中往往是不成立的，在属性个数比较多或者属性之间相关性较大时，分类效果不好。
• 对输入数据的表达形式很敏感。（上面讨论的都是离散值，如果是连续值需要转换）

三、实战演示

1. 垃圾邮件分类

原理

假设邮件的内容中包含的词汇为$W_i$，垃圾邮件Spam，正常邮件Ham。 判断一份邮件，内容包含的词汇为$W_i$，判断该邮件是否是垃圾邮件，即计算$P(S|W_i)$这个条件概率。
$P(Y=S)$: 垃圾邮件在训练数据集中的概率，或者实际调查的垃圾邮件出现的概率(即先验概率)；
$P(Y=H)$: 正常邮件在训练数据集中的概率，或者实际调查的正常邮件的分布；
$P(W_i\mid Y=S)$: 已知是垃圾邮件时，出现单词$W_i$的概率；包含单词的$W_i$的垃圾邮件个数/垃圾邮件总数。
$P(W_i\mid Y=H)$: 正常邮件中，词汇$W_i$出现的概率；
$P(S\mid W_i)$ : 出现单词$W_i$的邮件被判定为垃圾邮件的概率；

我们分别计算出$P(H|W)$和$P(S|W)$，比较它们的大小，就能判断是垃圾邮件还是正常邮件。

流程

下面基于朴素贝叶斯分类器实现的垃圾邮件分类。具体流程图如下

代码

if __name__ == '__main__':
    import pandas as pd

    df = pd.read_csv('./data/spam.csv')
    df.head()

    # 将标签数字化
    df['spam'] = df['Category'].apply(lambda x: 1 if x == 'spam' else 0)

    from sklearn.model_selection import train_test_split

    # 拆分训练集与测试集 可用来计算分数 得到分类器效果。k折叠交叉验证
    X_train, X_test, y_train, y_test = train_test_split(df.Message, df.spam, test_size=0.3,
                                                        random_state=7)
    from sklearn.feature_extraction.text import CountVectorizer

    # 将文本中的词语转换为词频矩阵
    v = CountVectorizer()
    # 通过fit_transform函数计算各个词语出现的次数  文本的预处理, 分词以及过滤停用词。可以使用tf–idf分词。
    X_train_count = v.fit_transform(X_train.values)

    # 该单词在整个训练的文集中出现的频率
    # print(v.vocabulary_.get("together"))

    # 导入多标签朴素贝叶斯模块
    from sklearn.naive_bayes import MultinomialNB

    # 实例化
    model = MultinomialNB()

    from sklearn import model_selection

    # 正对训练集做5次交叉验证，粗略查看效果
    score = model_selection.cross_val_score(model, X_train_count, y_train, cv=5)
    print(f"before scores:{score}\r\n")

    # 开始训练模型
    model.fit(X_train_count, y_train)

    # 转化测试集为数字
    X_test_count = v.transform(X_test.values)
    # 使用测试集预测
    y_pred = model.predict(X_test_count)

    from sklearn.metrics import recall_score, precision_score, accuracy_score

    # 在测试集上计算准确率
    model_accuracy_score = accuracy_score(y_test, y_pred)
    # 在测试集上计算精度 是分类器不将负样本标记为正样本的能力
    model_precision_score = precision_score(y_test, y_pred)
    # 在测试集上计算召回率 分类器找到所有正样本的能力
    model_recall_score = recall_score(y_test, y_pred)

    print(f"准确率:{model_accuracy_score}")
    print(f"精度:{model_precision_score}")
    print(f"召回率:{model_recall_score}\r\n")

    import joblib

    # save model
    joblib.dump(model, './out/rfc.pkl')
    # load model
    rfc2 = joblib.load('./out/rfc.pkl')

    # 测试
    emails = [
        'Hey mohan, can we get together to watch footbal game tomorrow?',
        'Upto 20% discount on parking, exclusive offer just for you. Dont miss this reward!'
    ]
    emails_count = v.transform(emails)
    # 预测
    result = rfc2.predict(emails_count)
    print(f"result:{result}\r\n")

2. 连续值特征

我们发现在之前的概率统计方式，都是基于离散值的。如果遇到连续型变量特征，怎么办呢？

一种处理方式是：把它转换成离散型的值。比如身高：180cm及以上为高。

但是，以上的划分方式，都比较粗糙，划分的规则也是人为拟定的，且在同一区间内的样本（比如身高变换规则下，身高180cm和185cm难以区分，我们有高斯朴素贝叶斯模型可以解决这个问题。

如果特征 $x_i$是连续变量，如何去估计似然度$P(x_i|y_k)$呢？高斯模型是这样做的：我们假设在$y_i$的条件下，$x$服从高斯分布（正态分布）。根据正态分布的概率密度函数即可计算出$P(x|y_i)$，公式如下：

$$P(x_i|y_k)=\frac{1}{\sqrt{2\pi {\sigma }_{yk,i}^2}}{e}^{-\frac{(x_i-{\mu }_{yk,i}{)}^2}{2{\sigma }_{yk,i}^2}}$$

${\mu }_{yk,i}$表示类别为$y_k$的样本中，第$i$维特征的均值。

${\sigma }_{yk,i}^2$表示类别为$y_k$的样本中，第$i$维特征的标准差。

例如防误触中运用的贝叶斯模型。触摸板坐标以及接触面积大小都是连续型变量，我需要计算数据的均值和标准差，来进行预测，因为都是标准数学计算，所以移植起来也非常简单。

四、拓展

1. 模型评估

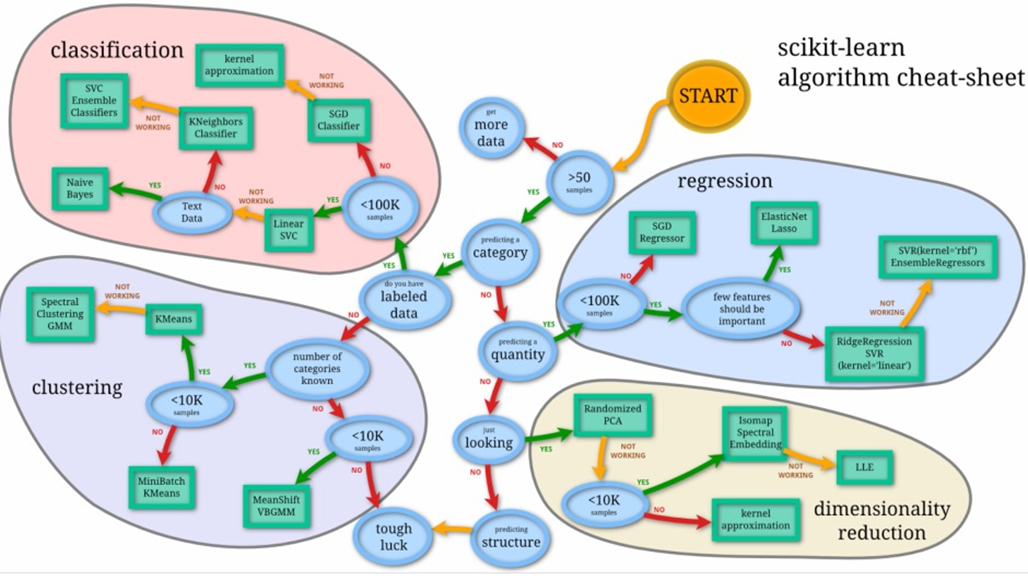
下图取自scikit-learn模型选择流程，可以参考参考。

分为四个大类

• classification：分类，预测类别。
• clustering：聚类，最常见的无监督学习算法。将同一类的数据尽可能聚集到一起，不同类数据尽量分离。
• regression：回归，通过训练得到样本特征到这些标签之间的映射，再用于预测数值型数据。
• dimensionality reduction：降维，是指在某些限定条件下，降低随机变量个数，得到一组“不相关”主变量的过程。更深层次的意义在于有效信息的提取综合及无用信息的摈弃。

---

基本概念

1. 概率论基础

• 条件概率（Conditional Probability）

​ 条件概率是指事件A在另外一个事件B已经发生条件下的发生概率。条件概率表示为：$P(A|B)$ 。

• 联合概率(Joint Probability)

​ 联合概率是指在多元的概率分布中多个随机变量分别满足各自条件的概率。假设X和Y都服从正态分布，那么P{X<4,Y<0}就是一个联合概率，表示X<4,Y<0两个条件同时成立的概率。表示两个事件共同发生的概率。A与B的联合概率表示为 $P(AB)$ 或者$P(A,B)$,或者$P(A\cap B)$。

• 先验概率（Prior Probability）

​ 先验概率是指根据以往经验和分析得到的概率，如全概率公式，它往往作为“由因求果”问题中的“因”出现的概率。

• 后验概率（Posterior Probability）

​ 后验概率是指在得到“结果”的信息后重新修正的概率，是“执果寻因”问题中的"因"。

​ 某件事已经发生，想要计算这件事发生的原因是由某个因素引起的概率。

​ 例如：已经发生了事件A，求事件A是由事件B引起的概率，表示为$P(A|B)$。

• 似然函数（likelihood of θ w.r.t. D）

​ 似然 是由结果推导条件，实验结果已知似然估计参数=b（具体值）的可能性

• 事件的独立性

​ 若 $A$, $B$ 独立，则 $P(AB)=P(A)P(B)$

2. 有监督 无监督 强化学习

​ 区分监督学习和无监督学习的最简单方法是查看数据是否被标记。

• 监督学习

​ 根据输入数据对定义的标签进行预测。它可以将数据分类为类别（分类问题）或预测结果（回归算法）。

• 无监督学习

​ 揭示了数据集中未明确呈现的潜在模式，它可以发现数据点的相似性（聚类算法）或发现变量的隐藏关系（关联规则算法）

• 强化学习

​ 另一种类型的机器学习，其中代理根据其与环境的交互来学习采取行动，目的是最大化奖励。它最类似于人类的学习过程，遵循试错法。

3. 常见的分布

数据分布，我们用连续（continuous）的形式来展示这些分布，分布可基本分为连续和离散。

• 均匀分布

​ 如图所示为均匀分布（uniform distribution）的例子。

上图对应的函数为 $$f(x)=\{\begin{array}{ll}1,& \text{0.0 ≤ x ≤ 1.0 }\\ 0,& \text{others}\end{array}$$

我们说如图所示的值在0～1的范围内是分布均匀的，或者说它们是常数（constant），亦或者说是平面（flat）的。这告诉我们，这个范围内的所有值是等概率的。

• 正态分布

最流行的分布是正态分布（normal distribution），也叫作高斯分布（Gaussian distribution），或者简单地称其为钟形曲线（bell curve）。与均匀分布不同，正态分布的曲线是平滑的，没有尖锐的拐角或者突然的跳跃。

• 伯努利分布

​ 另一个有用的特殊分布称为伯努利分布（Bernoulli distribution），这个离散分布只返回两个可能的值：0和1。伯努利分布的一个常见例子是抛掷硬币得到正反面的分布。
我们用字母 $p$ 来描述得到1的概率。由于两个概率相加必须得1（忽略奇怪的着陆情况，硬币必须正面或反面着陆），这意味着返回0的概率是 1−$p$。
如图直观地显示了抛掷一枚质地均匀的硬币和一枚质地不均匀的硬币的情况。

• 多项式分布

​ 伯努利分布只返回两个可能值中的一个，但是假如我们需要从更多数字（或者说更多的可能性）中返回一个呢？例如我们抛6面的筛子，我们就会返回1~6中的一个数字。

​ 这个分布是对两种输出的伯努利分布的推广，就称之为多项式分布（multinoulli distribution）,有时也简单称之为类别分布（categorical distribution）

4. 数学术语

• 标准差

  是离均差平方的算术平均数（即：方差）的算术平方根，用$\sigma$表示。

  总体标准差：$\sigma =\sqrt{\frac{{\sum }_{i=1}^n(x_i-\overline{x}{)}^2}{n}}$

---

参考

[1]朴素贝叶斯算法详解

[2]带你理解朴素贝叶斯分类算法

[3]scikit-learn处理文本数据