生成模型与判别模型
有监督机器学习方法可以分为生成模型 (generative approche) 与判别模型 (discriminative approche)。
Discriminative models draw boundaries in the data space, while generative models try to model how data is placed throughout the space. A generative model focuses on explaining how the data was generated, while a discriminative model focuses on predicting the labels of the data.
In mathematical terms, a discriminative machine learning trains a model which is done by learning parameters that maximize the conditional probability P(Y|X), while on the other hand, a generative model learns parameters by maximizing the joint probability of P(X, Y).
一言以蔽之,判别模型的工作是直接学习决策函数 f ( X ) f(X) f(X),或是估计 P ( Y ∣ X ) P(Y|X) P(Y∣X)。生成模型稍微绕了一下,通过估计 P ( X , Y ) P(X, Y) P(X,Y) 间接地得到 P ( Y ∣ X ) P(Y|X) P(Y∣X)(通过贝叶斯公式)。尽管生成模型较为复杂,但它的优势在于,它可以生成接近原数据分布的新的数据,因此得名。
常见的生成模型有:朴素贝叶斯、GAN(生成对抗网络)、LDA/QDA、HMM(隐马尔可夫模型)
常见的判别模型有:KNN、逻辑回归、MLP(多层感知机)、决策树、随机森林、SVM等。
一般我们对判别模型更熟悉,那这次就接触一点不一样东西——生成模型。
朴素贝叶斯
朴素贝叶斯(naïve Bayes)是基于贝叶斯定理与特征条件独立假设的分类方法。
对于给定的训练数据集,首先基于特征条件独立假设学习
P
(
X
,
Y
)
P(X, Y)
P(X,Y) ;然后基于此模型,对给定的输入
x
x
x,利用贝叶斯定理求出后验概率最大的输出y。
特征条件独立假设:输入X是一个n维向量(n个特征)
P
(
X
=
x
∣
Y
=
c
k
)
=
P
(
X
1
=
x
1
,
.
.
.
,
X
n
=
x
n
∣
Y
=
c
k
)
=
∏
i
=
1
n
P
(
X
i
=
x
i
∣
Y
=
c
k
)
P(X=x|Y=c_k) = P(X_1=x_1, ..., X_n=x_n |Y=c_k)= \prod_{i=1}^n P(X_i=x_i | Y=c_k)
P(X=x∣Y=ck)=P(X1=x1,...,Xn=xn∣Y=ck)=i=1∏nP(Xi=xi∣Y=ck)
这是一个非常强的假设,因此这个方法叫做naïve Bayes. 在此假设下,可以简化后验概率:
P
(
Y
=
c
k
∣
X
=
x
)
∝
P
(
Y
=
c
k
)
∏
i
=
1
n
P
(
X
i
=
x
i
∣
Y
=
c
k
)
P(Y=c_k | X=x) \propto P(Y=c_k) \prod_{i=1}^n P(X_i=x_i | Y=c_k)
P(Y=ck∣X=x)∝P(Y=ck)i=1∏nP(Xi=xi∣Y=ck)
通过极大似然法估计先验概率和条件概率,前者就是
y
y
y的各个类在训练集中的出现频率。朴素贝叶斯的分类结果是:
y
=
a
r
g
m
a
x
c
k
[
P
(
Y
=
c
k
)
∏
i
=
1
n
P
(
X
i
=
x
i
∣
Y
=
c
k
)
]
y = argmax_{c_k} [P(Y=c_k) \prod_{i=1}^n P(X_i=x_i | Y=c_k)]
y=argmaxck[P(Y=ck)i=1∏nP(Xi=xi∣Y=ck)]
基于对条件概率
P
(
X
i
=
x
i
∣
Y
=
c
k
)
P(X_i=x_i | Y=c_k)
P(Xi=xi∣Y=ck) 的不同分布假设,朴素贝叶斯可以分为许多种。我们简单看一下sklearn中实现的几种。
Gaussian Naive Bayes
高斯朴素贝叶斯,假设条件概率满足高斯分布:
P
(
X
i
=
x
i
∣
Y
=
c
k
)
]
=
1
2
π
σ
c
k
e
x
p
(
−
(
x
i
−
μ
i
)
2
2
σ
c
k
2
)
P(X_i=x_i | Y=c_k)] = \frac{1}{\sqrt{2\pi \sigma_{c_k}}} exp(-\frac{(x_i-\mu_i)^2}{2 \sigma_{c_k}^2})
P(Xi=xi∣Y=ck)]=2πσck1exp(−2σck2(xi−μi)2)
Multinomial Naive Bayes
多项分布朴素贝叶斯,以及之后提到的互补朴素贝叶斯,是两种常用的文本分类器。它们简单易实现,常作为baseline,与其他复杂的文本分类算法比较。典型的应用场景包括垃圾邮件分类、产品标签分类等。
sklearn的文档把公式列得很清楚:Multinomial Naive Bayes
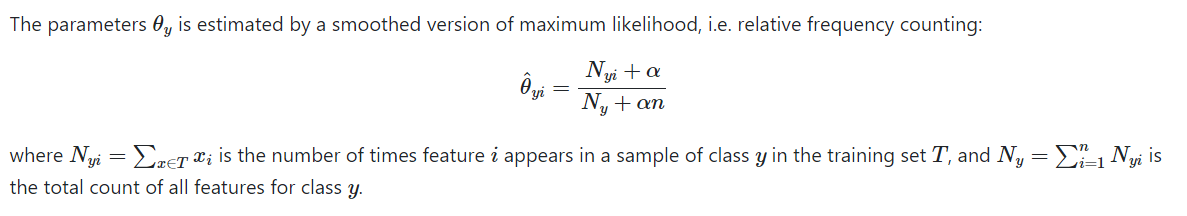
i i i is the word index (in case of text classification), y y y indicates the class. In case of spam email classification, y ∈ { spam , not spam } y \in \{\text{spam}, \text{not spam} \} y∈{spam,not spam}.
这里的参数 θ y i \theta_{yi} θyi 反映的是单词 i i i出现的相对频率,是极大似然法结果的平滑版本,防止出现 θ y i = 0 \theta_{yi}=0 θyi=0 的情况。
Complement Naive Bayes
互补朴素贝叶斯(CNB)是多项分布朴素贝叶斯(MNB)的修改版本,在非平衡的数据集上做了改进。在文本分类的任务上,CNB往往优于MNB。sklearn文档:Complement Naive Bayes

这次的
θ
c
i
\theta_{ci}
θci(对应上面的
θ
y
i
\theta_{yi}
θyi)计算的是单词
i
i
i出现在不同于类别
c
c
c的文档中的频率。这个频率越高,说明单词
i
i
i 越“不属于”类别
c
c
c.
sklearn文档中没有解释公式最后一行的
t
i
t_i
ti,通过查阅原论文,发现
t
i
t_i
ti 指的是单词
i
i
i 在当前要分类的文本中出现的次数。
CNB提到, d i j d_{ij} dij 不仅可以使用单词的出现次数,也可以用TF-IDF。那什么是TF-IDF?这就作为本篇的一个拓展吧。
拓展:TF-IDF
Term Frequency–Inverse Document Frequency (TF-IDF) 是 word count vector 之外,另一种编码文档单词的方式。下图是 word count vector 编码的示例,它统计每个单词在每个文档中出现的次数。
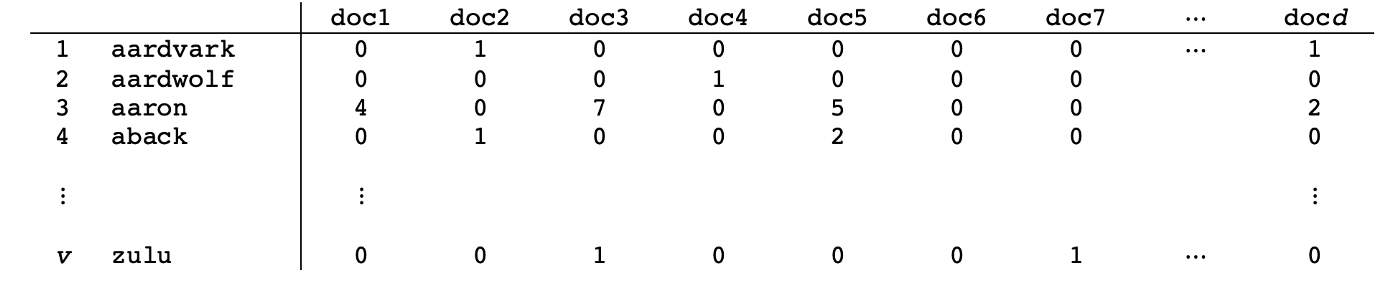
而 TF-IDF 是由两项——TF 和 IDF——相乘得到的。
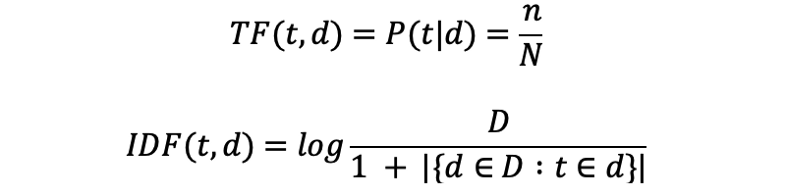
t
t
t 代表单词;
d
d
d 代表文档;
n
n
n 代表单词
t
t
t 在文档
d
d
d 中出现的次数;
N
N
N 是单词
t
t
t 在所有文档中出现的总次数。
D
D
D 代表所有文档的个数;
∣
{
d
∈
D
:
t
∈
d
}
∣
|\{d \in D : t \in d\}|
∣{d∈D:t∈d}∣ 代表出现过单词
t
t
t 的文档个数。
直观来理解:给定单词 t t t 和文档 d d d ,该单词在该文档中出现的相对次数越多,它对于该文档越重要(TF一项);同时,如果该单词也出现在了很多其他文档中,那么它对于该文档的重要性会随之下降(IDF一项)。
相对于 word count vector 编码,TF-IDF的编码方式限制了对常用词给予过多的权重。以英文单词为例,诸如the, a, and 等词在每篇文章的出现频率都会高。word count vector 编码方式会对这些词在所有文档中统统给予很高权重。而TF-IDF通过IDF这项,可以极大限制这些词的权重(比如每篇文章中都出现了单词 a ,此时
∣
{
d
∈
D
:
t
∈
d
}
∣
=
D
|\{d \in D : t \in d\}| = D
∣{d∈D:t∈d}∣=D,IDF一项趋近于0)。
LDA/QDA
LDA (Linear Discriminant Analysis), QDA (Quadratic Discriminant Analysis) 是另两种生成模型分类算法。它们的思路是一样的:把 P ( x ∣ y ) P(x|y) P(x∣y) 建模为多维高斯分布。
sklearn: Linear and Quadratic Discriminant Analysis 文档写得很详细
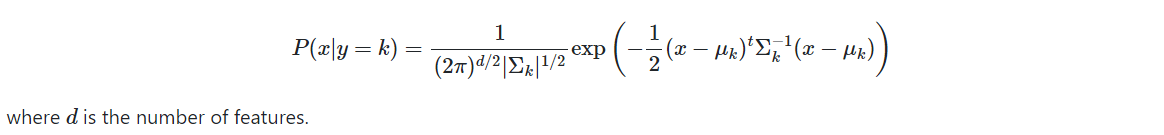
μ
k
∈
R
d
,
Σ
k
∈
R
d
×
d
\mu_k \in \mathbb{R}^d, \Sigma_k \in \mathbb{R}^{d \times d}
μk∈Rd,Σk∈Rd×d
QDA
根据贝叶斯定理:
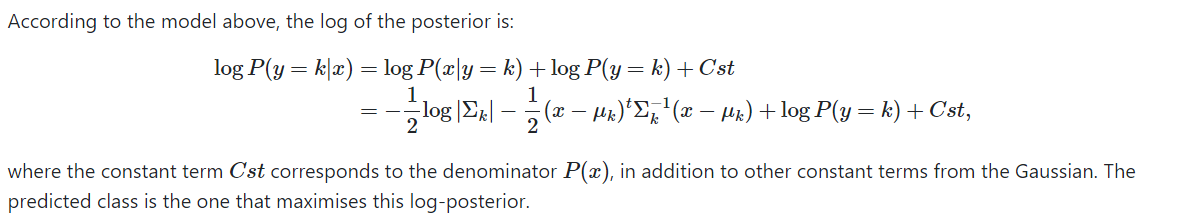
注意:如果假设那些协方差矩阵
Σ
k
\Sigma_k
Σk 都是对角矩阵,即每个类中
x
x
x 的特征都是相互独立的,这恰好是朴素贝叶斯的假设。因此在该假设下,QDA等价于高斯朴素贝叶斯(GNB)。
LDA
如果说GNB是QDA的一个特例,那么LDA就是QDA的另一个特例。LDA假设每个类中的协方差矩阵都是一样的。
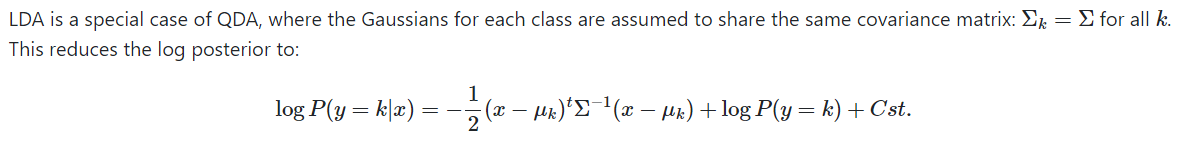





















 2363
2363











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








