代码规范
小驼峰命名法命名变量;大驼峰命名法命名类名、属性名等。
代码留白:(整体风格)
void moveZeros(vector<int>& nums){
int slowIndex = 0;
for (int fastINdex = 0; fastIndex < nums.size(); fastIndex++){
if (nums[fastIndex] != 0) {
nums[slowIndex++] = nums[fastIndex];
}
}
for (int i= slowIndex; i < nums.size(); i++){
nums[i] = 0;
}
}
数据结构与算法
1.绪论
1.1抽象数据类型(ADT)
定义格式:
ADT 抽象数据类型名{
Data
数据对象的定义
数据元素之间逻辑关系的定义
Operation
操作1
初始条件
操作结果描述
操作2
······
操作n
}ADT 抽象数据类型名
圆抽象数据类型定义(伪代码):
ADT Circle{
数据对象:D = {r,x,y|r,x,y均为实数}
数据关系:R = {<r,x,y>|r是半径,<x,y>是圆心坐标}
基本操作:
Circle(&C,r,x,y)
操作结果:构造一个圆。
double Area(C)
初始条件:圆已存在
操作结果:计算面积
double Circumference(C)
初始条件:圆已存在
操作结果:计算周长
······
}ADT Circle
1.2 算法和算法分析
算法的定义:
算法是解决特定问题求解步骤的描述,在计算机指令中为指令的有限序列,并且每条指令表示一个或多个操作。
算法的特性:
- 有穷性、确定性、可行性、输入、输出。
算法设计的要求:
- 正确性(Correctness) 可读性(Readablility) 健壮性(又称鲁棒性)(Robustness) 高效性(Efficiency)
算法的度量方法:
事后统计方法(不科学、不准确)、事前分析估算方法。
算法的效率:
- 时间效率:指的是算法所耗费的时间;
- 空间效率:指的是算法执过程中所耗费的储存空间。
1.时间效率度量
算法举例(两个n*n的矩阵相乘):
for(int i=1;i<=n;i++) //执行n+1次
{
for(int j=1;j<=n;j++) //n(n+1)次
{
c[i][j]=0; //n*n次
for(int k=0;k<n;k++) //n*n*(n+1)次
{
c[i][j]=c[i][j]+a[i][k]*b[k][j];//n*n*n次
}
}
}
上述算法时间消耗为:
T
(
n
)
=
2
n
2
+
3
n
2
+
2
n
+
1
T(n)=2n^2+3n^2+2n+1
T(n)=2n2+3n2+2n+1
时间复杂度的渐进表示法主要比较它们的数量级;(时间复杂度,上述算法的时间复杂度为它的时间消耗公式的数量级)如下:
T
(
n
)
=
O
(
n
3
)
T(n)=O(n^3)
T(n)=O(n3)
数量级分类:

常用的时间复杂度所耗费的时间从小到大依次是:
- 常数阶->对数阶->线性阶 >线性对数阶->平方阶->立方阶->K次方阶->指数阶->阶乘阶
2.空间效率度量
例:将一维数组a中的n个数逆序放到原数组中
算法一:原地工作,空间复杂度为常数阶
for(int i=0;i<n/2;i++)
{
t = a[i];
a[i] = a[n-i-1];
a[n-i-1] = t;
}
算法二:空间复杂度为线性阶
for(int i = 0;i<n;i++)
b[i]=a[n-i-1];
for(int i = 0;i<n;i++)
a[i] = b[i];
3.扩展:递归算法的时间复杂度分析
面试题:求x的n次方
1)最直观的方法是通过一个for循环求出结果,代码如下:(该算法时间复杂度为O(n))
int function1(int x, int n) {
int result = 1; //注意任何数的0次方都等于1
for (int i = 0; i < n; i++) {
result = result * x;
}
return result;
}
2)使用递归算法解决:
该算法每次递归n都做以此减1的操作,那么就是递归了n次,时间复杂度是O(n),每次执行一个乘法操作,而乘法操作的时间复杂度是一个常数项O(1),所以这段代码的时间复杂度是O(n)(O(1))=O(n)
int function2(int x, int n) {
if (n == 0) {
return 1; //return 1,同样是因为任何数的0次方都等于1
}
return function2(x, n-1) * x;
}
3)二叉树型递归算法:(这段代码的时间复杂度又是多少呢?)
int function3(int x, int n) {
if (n == 0){
return 1;
}
if (n % 2 == 1) {
return function3(x, n/2) * function3(x, n/2)*x;
}
return function3(x, n/2) * function3(x, n/2);
}
首先看递归了多少次。可以把递归的次数抽象为一颗满二叉树,用一颗满二叉树来表示这个算法,如图:
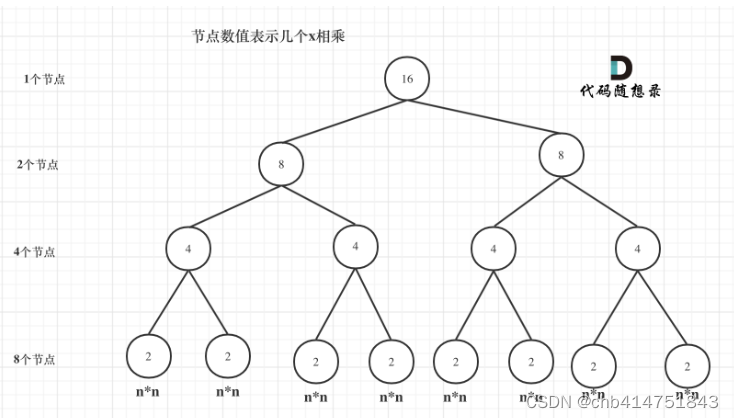
当前这棵二叉树就是求x的n次方(为了方便表示n为偶数),当n为16的时候,执行了多少次乘法运算操作呢?这棵树上的每一个节点就代表一次递归并执行了一次相乘操作,所以执行了多少次递归操作,就是看这棵树上有多少个节点。这棵满二叉树的节点数量是
2
3
+
2
2
+
2
1
+
2
0
=
15
2^3+2^2+2^1+2^0=15
23+22+21+20=15
可以发现,这其实就是等比数列的求和公式。(int n = 1 % 2; // n为1,int n = 1/2; //n为0)
如果求x的n次方,即设有m层,就有
2
m
+
2
m
−
1
+
.
.
.
+
2
0
=
2
m
+
1
−
1
2^m+2^{m-1}+...+2^0 = 2^{m+1}-1
2m+2m−1+...+20=2m+1−1
个树节点,又(2的m+1次方等于n)
m
=
l
o
g
2
n
−
1
m = log_2n-1
m=log2n−1
得,总节点数为n-1个。
此时,这个递归算法的时间复杂度依然是O(n)。
4)记忆递归算法:
int function4(int x, int n) {
if (n == 0) {
return 1;
}
int t = function4(x, n/2);//相当于function3,这里是把递归操作抽取出来
if (n % 2 == 1) {
return t*t*x;
}
return t*t;
}
这里只有一个递归调用,而且每次递归操作的数据规模都除以2,所以这里一共调用了
l
o
g
2
n
log_2n
log2n
次,每次递归都是一次乘法操作,所以这个递归算法的时间复杂度为O(logn)。
4.扩展:递归算法的空间复杂度分析
- 递归算法的时间复杂度 = 每次递归的时间复杂度 * 递归次数
- 递归算法的空间复杂度 = 每次递归的空间复杂度 * 递归深度
例题:求斐波那契数列的性能分析
1.递归算法
int fibonacci(int i) {
if (i <= 0) return 0;
if (i == 1) return 1;
return fibonacci(i-1) + fibonacci(i-2);
}
测量输入n时候,这段递归求斐波那契数列代码的耗时:
#include <iostream>
#include <chrono>
#include <thread>
using namespace std;
using namespace chrono;
int fibonacci(int i) {
if(i <= 0) return 0;
if(i == 1) return 1;
return fibonacci(i - 1) + fibonacci(i - 2);
}
void time_consumption() {
int n;
while (cin >> n) {
milliseconds start_time = duration_cast<milliseconds >(
system_clock::now().time_since_epoch()
);
fibonacci(n);
milliseconds end_time = duration_cast<milliseconds >(
system_clock::now().time_since_epoch()
);
cout << milliseconds(end_time).count() - milliseconds(start_time).count()
<<" ms"<< endl;
}
}
int main()
{
time_consumption();
return 0;
}
2.优化递归算法
int fibonacci(int first, int second, int n) {
if (n <= 0) {
return 0;
}
if (n < 3) {
return 1;
}
else if (n == 3) {
return first + second;
}
else {
return fibonacci(second, first + second, n-1);
}
}
测量这段递归求斐波那契数列代码的耗时:
#include <iostream>
#include <chrono>
#include <thread>
using namespace std;
using namespace chrono;
int fibonacci_3(int first, int second, int n) {
if (n <= 0) {
return 0;
}
if (n < 3) {
return 1;
}
else if (n == 3) {
return first + second;
}
else {
return fibonacci_3(second, first + second, n - 1);
}
}
void time_consumption() {
int n;
while (cin >> n) {
milliseconds start_time = duration_cast<milliseconds >(
system_clock::now().time_since_epoch()
);
fibonacci_3(1, 1, n);
milliseconds end_time = duration_cast<milliseconds >(
system_clock::now().time_since_epoch()
);
cout << milliseconds(end_time).count() - milliseconds(start_time).count()
<<" ms"<< endl;
}
}
int main()
{
time_consumption();
return 0;
}
3.普通方法
int fibonacci(int n) {
int a = 0, b = 1;
while (n--) {
int c = a + b;
a = b, b = c;
}
return a;
}
各种方法性能分析:
| 求斐波那契数 | 时间复杂度 | 空间复杂度 |
|---|---|---|
| 递归算法 | O(2^n) | O(n) |
| 优化递归算法 | O(n) | O(n) |
| 普通方法 | O(n) | O(1) |
1.3 课后例题
1.1 选择问题:寻找N个元素中的第K个最大值。下面代码令K = N/2 。
#include <iostream>
using namespace std;
#include<vector>
#include<algorithm>
#define ArrayNum 10
#define ResultNum (ArrayNum/2)
int main()
{
// 从原始数组中取出ResultNum各元素,然后进行降排序
vector<int> v;
int array[ArrayNum] = { 9, 3, 10, 2, 25, 7, 8, 14, 17, 12 };
cout << "排序前:" << endl;
for (int i = 0; i < ArrayNum; i++)
{
cout<<array[i]<<" ";
v.push_back(array[i]);
}
sort(v.begin(), v.end(), greater<int>());//排序算法,降序
cout << endl;
cout << "排序后:"<<endl;
for (vector<int>::iterator it = v.begin(); it != v.end(); it++)
{
cout << *it << " ";
}
cout << endl;
cout << "第k个最大值为:" << v[ResultNum-1]<<endl;
return 0;
}




















 761
761











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








