【NOIP2016提高A组集训第1场10.29】配对游戏

题目

流行的跳棋游戏是在一个有m*n个方格的长方形棋盘上玩的。棋盘起初全部被动物或障碍物占满了。在一个方格中，‘X’表示一个障碍物，一个‘0’～‘9’的个位数字表示一个不同种类的动物，相同的个位数字表示相同种类的动物。一对动物只有当它们属于同一种类时才可以被消去。消去之后，他们所占的方格就成为空方格，直到游戏结束。要消去一对动物的前提条件是：这对候选动物所在的方格必须相邻，或它们之间存在一条通路。棋盘上一个方格只和其上下左右的方格相邻。一条通路是由一串相邻的空方格组成。路的长度则是通路中空方格的数目。你要输出可被消去的动物的最多对数，以及在此操作过程中，最小的通路长度总和。
例1 如下的一个3*4棋盘：

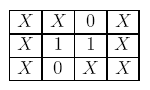
两个种类为“1”的动物可以被消去，因为它们相邻，通路的长度是0。在这一步骤之后，存在一条在两个种类为“0”的动物间的长度为2的通路，所以这两个动物也可以被消去。要消去这2对动物，通路的长度总和是 0+2=2。这也是最小的通路长度总和，因为这是唯一一个消去这2对动物的方法。所以答案是 2 2。
例2 如下的一个4*1棋盘:

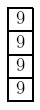
如果我们先消去正中间的两个种类为“9”的动物，然后消去最上面和最下面的两个种类为“9”的动物，则累计通路长度为 0+2=2。但是，我们可以先消去最顶上的两个，然后再消去最底下的两个。同样也消去了2对动物，但通路长度总和是 0+0=0。很明显，长为0的通路长度总和是最短的，答案应是 2 0。

分析

暴力，加个判重。
因为只有25个格子，将每个格子是否消掉化成二进制状态，
记录这个状态的最优答案。
用正确率换时间，随便坑坑就过了。
还跑到特别快，我自己都惊呆了。

#include <cmath>
#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <algorithm>
#include <queue>
const int maxlongint=2147483647;
const int mo=1000000007;
const int N=7;
using namespace std;
int c[11][37][2],a[N][N],ans,n,m,ans1;
short int hash[33554532][2];
int zz[4][2]=
{
 {0,1},
 {1,0},
 {0,-1},
 {-1,0}
};
inline int dg1(int b[N][N],int x,int y,int v,int dis[N][N])
{
    for(int i=0;i<=3;i++)
    {
        int xx=zz[i][0]+x,yy=zz[i][1]+y;
        if(xx<1 || xx>n || yy<1 || yy>m) continue;
        if(b[xx][yy]==11)
        {
            if(dis[xx][yy]>dis[x][y]+1) dis[xx][yy]=dis[x][y]+1,dg1(b,xx,yy,v,dis);
        }
        else
        if(b[xx][yy]==v)
        {
            dis[xx][yy]=min(dis[x][y]+1,dis[xx][yy]);
        }
    }
}
inline int dg(int b[N][N],int v,int sum)
{
    int num=0;
    for(int i=1;i<=n;i++)
        for(int j=1;j<=m;j++)
        {
            if(b[i][j] && b[i][j]!=11) num+=1<<((i-1)*m+j-1);
        }
    if(!hash[num][0])
    {
        hash[num][0]=sum;
        hash[num][1]=v;
    }
    else
    {
        if(hash[num][0]>sum) return 0;
        if(hash[num][0]==sum && hash[num][1]<=v) return 0;
        hash[num][0]=sum;
        hash[num][1]=v;
    }
    bool q=true;
    int dis[N][N],mn;
    for(int i=1;i<=n;i++)
        for(int j=1;j<=m;j++)
        {
            if(b[i][j] && b[i][j]!=11)
            {
                memset(dis,43,sizeof(dis));
                dis[i][j]=0;
                dg1(b,i,j,b[i][j],dis);
                int g=b[i][j];
                mn=maxlongint;
                for(int k=1;k<=c[g][0][0]-1;k++)
                    for(int l=k+1;l<=c[g][0][0];l++)
                    {
                        if(dis[c[g][k][0]][c[g][k][1]]>dis[c[g][l][0]][c[g][l][1]])
                        {
                            int o=c[g][k][0];
                            c[g][k][0]=c[g][l][0];
                            c[g][l][0]=o;
                            o=c[g][k][1];
                            c[g][k][1]=c[g][l][1];
                            c[g][l][1]=o;
                        }
                    }
                for(int k=1;k<=c[g][0][0];k++)
                    if(dis[c[g][k][0]][c[g][k][1]]!=dis[0][0] && b[c[g][k][0]][c[g][k][1]]==b[i][j] && (i!=c[g][k][0] || j!=c[g][k][1]))
                    {
                        b[i][j]=b[c[g][k][0]][c[g][k][1]]=11;
                        dg(b,v+dis[c[g][k][0]][c[g][k][1]]-1,sum+1);
                        q=false;
                        b[i][j]=b[c[g][k][0]][c[g][k][1]]=g;
                    }
            }
        }
    if(q)
    {
        if(sum>ans)
        {
            ans=sum;
            ans1=v;
        }
        else
        if(sum==ans && ans1>v) ans1=v;
        return 0;
    }
}
int main()
{
    scanf("%d%d",&n,&m);
    for(int i=1;i<=n;i++)
        for(int j=1;j<=m;j++)
        {
            char ch=getchar();
            while((ch<'0' || ch>'9') && ch!='X') ch=getchar();
            if(ch>='0' && ch<='9')
            {
                a[i][j]=ch-47;
                c[ch-47][0][0]++;
                c[ch-47][c[ch-47][0][0]][0]=i;
                c[ch-47][c[ch-47][0][0]][1]=j;
            }
        }
    ans=0;
    ans1=maxlongint;
    dg(a,0,0);
    printf("%d %d",ans,ans1);
}