高斯消去法
高斯消去法主要用于求解线性方程组的解,但由于算法相对复杂,因此常用于低阶稠密方程组(个人理解稠密即为方程组中的系数项为0的个数少,也就是系数矩阵A零元素的个数少,反之则为稀疏方程组)。
如已知一个n元n次的方程组,代数形式即可写成如下形式:
我们可以将其转化为矩阵形式(Ax=b),其中A为系数矩阵,如下:
基本思想:
首先通过逐次消元法将Ax=b化为等价的上三角形方程组(即系数矩阵A中对角线以下的元素都为0),再求解这个上三角的方程组。(个人认为这个高斯消去法最大的好处是可以在计算机上实现,方便编程。)








 高斯消元法是求解线性方程组的一种方法,尤其适用于低阶稠密方程组。它通过消元将方程组转化为上三角形形式,然后进行回代求解。在实际应用中,为了考虑计算误差和代码效率,出现了多种改进算法,如列主元法、全主元法、LU分解法等。
高斯消元法是求解线性方程组的一种方法,尤其适用于低阶稠密方程组。它通过消元将方程组转化为上三角形形式,然后进行回代求解。在实际应用中,为了考虑计算误差和代码效率,出现了多种改进算法,如列主元法、全主元法、LU分解法等。
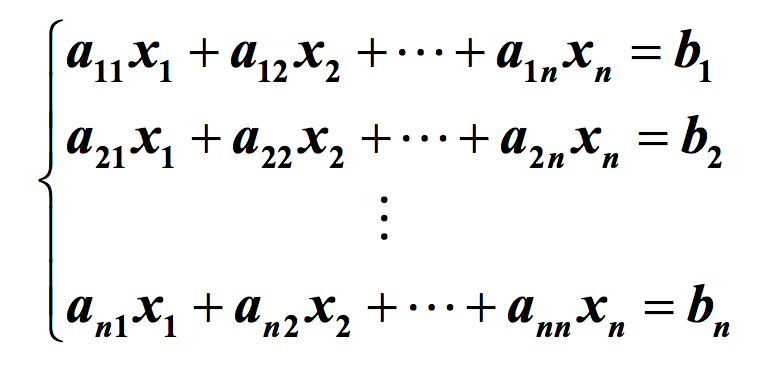
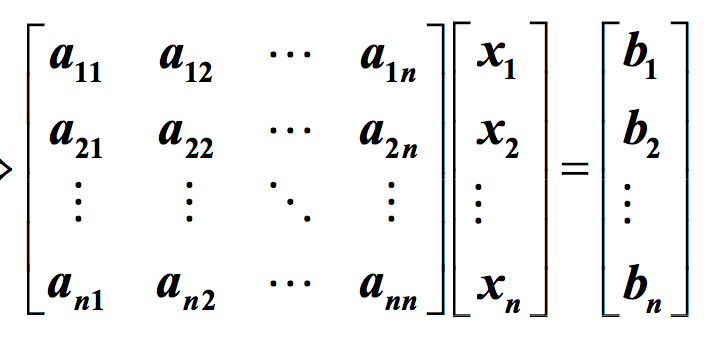
 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章

















 7846
7846

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








