Matlab fftshift and ifftshift and some confusions

最新推荐文章于 2024-10-17 23:00:18 发布

笨牛慢耕

最新推荐文章于 2024-10-17 23:00:18 发布

阅读量1.8k

点赞数 10

分类专栏： Matlab 信号处理与数字通信文章标签：经验分享 matlab fftshift

本文链接：https://blog.csdn.net/chenxy_bwave/article/details/119185124

版权

Matlab 同时被 2 个专栏收录

24 篇文章

订阅专栏

信号处理与数字通信

15 篇文章

订阅专栏

本文详细介绍了fftshift和ifftshift函数在MATLAB中的作用，它们主要用于在FFT运算后调整频域数据的布局，使零频分量位于中间。虽然常被误认为是逆操作，但fftshift和ifftshift在数组长度为奇数时并不互为逆操作。此外，文章指出在一般情况下，直接调用fft()并不需要先进行fftshift()预处理，其主要目的是为了使频谱显示更加直观。最后，通过代码示例验证了这一观点。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

1. 基本功能

“fftshift()”的功能是交换一个数组（为了简便期间，本文只考虑一维数组）的前后半区。主要的使用场景是在进行FFT运算以后将频域数据的零频分量挪到中间，使得频域数据的显示效果更符合自然的感觉。这是因为FFT运算输出的频域数据块中前半部分对应于非负频率分量（其中，第一个数据对应零频分量），而后半部分实际上对应负频率分量。因此如果不做调整直接进行显示的话，看上去得到的频谱图的频率范围对应于[0, Fs(1-1/Nfft)]范围。以下是一个示例。

clear; close all; clc
echo on

Fs = 100; % 100Hz
Ts = 1/Fs;
Nfft = 1024;
t  = Ts * (0:1:Nfft-1);
f1 = 7;
f2 = 17;
f3 = 37;
x  = sin(2*pi*f1*t) + 0.5*sin(2*pi*f2*t) + 0.2*sin(2*pi*f3*t); % Three frequency components with difference amplitude
X  = fft(x);

figure;
f_bins_direct = (0:1:1023) * Fs/Nfft;
subplot(2,1,1); plot(f_bins_direct,abs(X)); title('Direct display of the spectrum'); grid on;
f_bins_convert= fftshift(f_bins_direct);
f_bins_convert(f_bins_convert>=Fs/2) = f_bins_convert(f_bins_convert>=Fs/2) - Fs; 
subplot(2,1,2); plot(f_bins_convert,abs(fftshift(X))); title('Display of the spectrum after fftshift'); grid on;

运行所得的结果如下图所示：

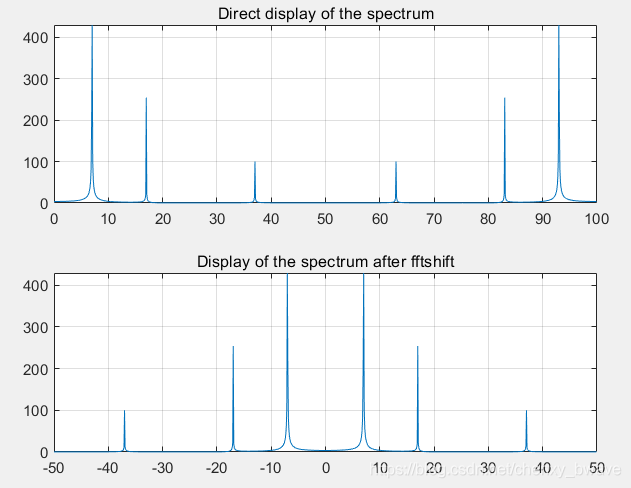
图 1 两种不同的频谱图显示

Matlab内置的频谱计算和显示工具都封装了fftshift()处理，可以通过选项控制如何显示频谱。以下是一个使用pwelch进行频谱分析的例子。

%% pwelch's option "centered"
x  = exp(j*2*pi*f1*t) + 0.5*exp(j*2*pi*f2*t) + 0.2*exp(j*2*pi*f3*t); % Three frequency components with difference amplitude
figure; pwelch(x,[],[],[],Fs,'centered'); title('Display double-sided spectrum by specifying "centered"');

图2 pwelch display example with option "centered"

“ifftshift()”的功能与“fftshift()”相似，但是存在一些细微的差异，将在下一节说明。

2. 并非自己的逆操作

一个常见的误解是fftshift()和ifftshift()是完全相同的操作，而且是自己的逆操作—即针对某个数组连续两次调用fftshift()或者ifftshift()能够恢复原数据。然而并不是！fftshift()和ifftshift()是相互为逆操作，两者的作用完全抵消，但是两者有细微的差距，各自也并非自己的逆操作—否则的话，matlab为什么要设置这么两个函数？执行以下代码可以看到，x1与x0完全相同，x2和x3则与x0不同。

x0 = [1 2 3 4 5 6 7]
x1 = ifftshift(fftshift(x0))
x2 = fftshift(fftshift(x0))
x3 = ifftshift(ifftshift(x0))

原因可以从以下fftshift()源代码和ifftshift()源代码得知（为简单期间，这里只摘取了一维情况的处理。要看完整的代码可以在matlab窗口输入edit fftshift）。

% fftshift(x)
%     x = circshift(x,floor(size(x)/2));
% 
% ifftshift(x)
%     x = circshift(x,ceil(size(x)/2));

如上所示，fftshift和ifftshift内部都是调用循环以为函数实现，不同的是循环移位的量的计算略有细微差别。一个是数组长度除以2向下取整，另一个是数组长度除以2向上取整。在输入数组长度为偶数时，两者其实是完全相同的，且各自也是自己的逆操作。但是在输入数组长度为奇数时，情况有一点微妙的不同。比如说在以上例子中，长度为7，所以调用fftshift相当于循环右移3个数据，再次调用还是循环右移3个数据，总共循环右移量为6小于原数组长度，因此没有还原。而连续调用fftshift和ifftshift则可以保证总的循环右移量等于原数组长度因此可以还原原数组。简而言之，在数组长度为偶数时，fftshift和ifftshift的处理效果完全，且各自也是自己的逆操作；在数组长度为奇数时，fftshift和ifftshift的处理效果有细微差别，且各自也不是自己的逆操作。但是在任意长度条件下，fftshift和ifftshift都是互为逆操作。

以下代码段对此进行一个简单的随机验证。随机生成长度，并基于该长度生成一个随机的数组，验证连续两次调用fftshift（或ifftshift）是否能够还原原数组，以及fftshift和ifftshift处理是否相互抵消。

for k = 1:1:100
    L = randi([10,100]); % 随机生成一个整数作为接下来数组生成的长度
    x = rand(1,L);  % 生成一个长度为L的随机数组
    if mod(L,2) == 0
        assert(isequal(fftshift(fftshift(x)),x)); % 判断fftshift(fftshift(x))与x是否完全相等，不相等则报错退出
    else
        assert(~isequal(fftshift(fftshift(x)),x)); % 判断fftshift(fftshift(x))与x是否不相等，相等则报错退出
    end
    fprintf(1,'k = %d, pass the test...\n',k);
end

代码中用两条assert()语句进行检查(1)数据长度为偶数时连续调用两次fftshift()恢复原数据；(2) 数据长度为奇数时连续调用两次fftshift()不能恢复原数据；运行这段代码如果没有报错的话就表示通过了测试，(1)和(2)成立。

3. Is fftshift() before fft() necessary?

Reference

https://www.mathworks.com/matlabcentral/answers/288818-what-s-the-purpose-of-doing-fftshift-twice
https://stackoverflow.com/questions/32166879/do-i-need-to-call-fftshift-before-calling-fft-or-ifft
https://www.cnblogs.com/zxhyxiao/p/12359243.html
Computational fourier optics : a MATLAB tutorial / David G. Voelz. P18-21
Wu, Kan: Why use fftshift(fft(fftshift(x))) instead of fft(x) in Matlab?

在网上碰到有人讨论这个问题，看起来似乎其中一个起源是来自于(4).

翻阅了一些讨论的帖子，我先根据我的理解给出一个简单的结论：在一般情况下，在fft()之间先对输入数据进行fftshift()处理是没有必要的。没有什么必然性。fftshift()这个函数的存在的目的并不是为了这个，单纯地就是上面所说的为了让频谱观测显得更自然一些而已。

在(3),(4),(5)（其中(3)只是对(4)的解读）给出了一些例子来说明为什么“需要”在调用fft()之前先对输入数据进行fftshift()处理。但是在我看来这些都没有必然性，或者说并不是绝对必须的。这里先给出一个简单的解释（有时间再来补详细的解释）。这是从根本上来说是因为fft()处理的离散数据，进行的是离散傅里叶变换（DFT）。如果所要解析的数据本身就是一个离散周期性信号，那fft()给出的结果就反映了真实情况。但是现实应用中，我们所分析的信号并不是离散周期性信号，而我们所能做的又只能是调用fft()执行离散傅里叶变换进行分析，这种情况下fft()结果并没有完全反映真实情况，而是一种近似的或者“变形”的体现。这个时候我们就需要对fft()结果进行合理的解释间接地得到真实的情况，某种意义上fftshift()将频域数据前后半颠倒以使得频域数据显示出来的效果显得更自然也是属于这种情况。

比如说，(4)中给出的例子是对对称时域信号进行调用fft()处理，然后将其结果与傅里叶变换的理论解析结果进行对比。原始信号的时间区间是[-T/2, T/2]，这个数据采样后直接用fft()进行处理的话，由于fft()自然地认为数据是从t=0开始，所以可以理解为fft()的输入数据其实是将原始信号在时域上右移T/2所得到的信号，而fft()的变换结果则代表着这个时域上右移T/2所得到的信号的周期性拓展后的信号的离散时间傅里叶变换（DTFT）的一个周期内的数据。接下来从这个结果进行解析可以反推得到原始信号的傅里叶变换结果。在fft()之前做fftshift()可以看作是一个小的trick, as an alternative to the post-analysis of the fft() result, without physical significance and necessity.