关于数值分析这门课程,很多同学感觉学起来十分吃力,所以在此给出数值分析学习内容的概览(国内研究生基本一样)以及作者自己学习时的一些总结,希望对您的学习有所脾益,相互进步。
写在前面
数值分析的核心思想(作者自己得出的结论,仅供参考)是:把人类历史上灿若星河的数学大神的解题方法转换成由计算机快速求解近似值的方法,一切都是近似,真值存在就是人类无法求出 ,哪里有近似哪里就有误差,知道这些基本思路,就比较容易理解数值分析整本书在干嘛了,就是把理论方法转换成计算机的算法,如是而已。
正文
废话少说,先贴上一幅自己做的内容图。
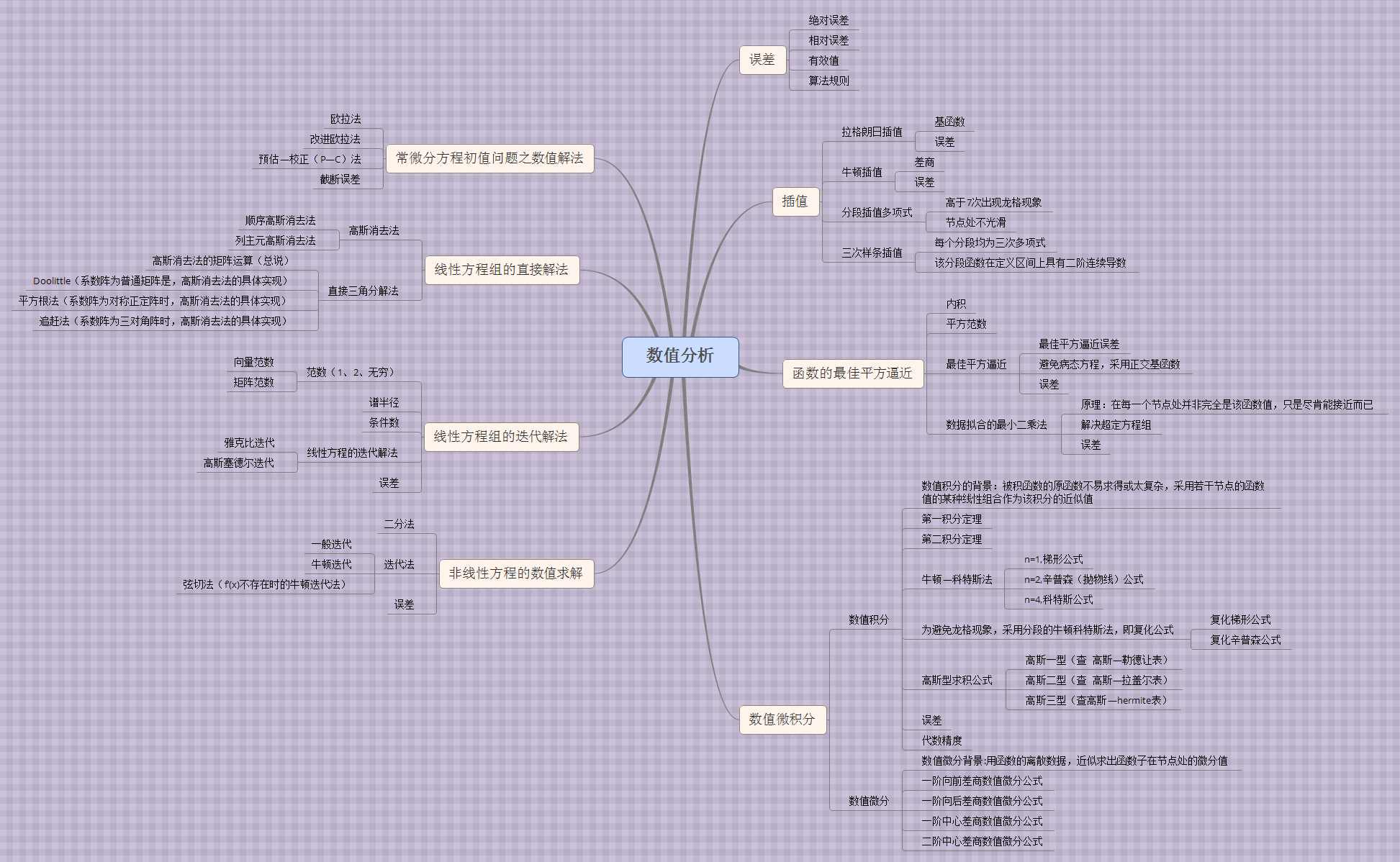
从右上角开始,顺时针浏览,这也是我学习这门课程时的顺序。数值分析全部内容看似独立成章,实则每一章有着千丝万缕的牵连。教材基本都是把最为基础和通用的部分放在第一章,所以误差及运算规则就落户在我们这张图的最开端。这一章最常考察的内容是有效值。有效值、绝对误差,相对误差三者之间的关系就是:知二求一。具体怎么实现,客官只需随便找一例题即可。

对于第二种插值,从概览图可以看出里面包含的内容。牛顿插值是对朗格朗日插值的一种优化。拉格朗日插值在额外增加数据时,无法利用之前计算的数据,故牛顿法的提出就是来克服这一问题。牛顿插值可以利用前面计算的数据,来计算你所需要的数据。比如,给出(1,2),(4,9)(-10,5)…让你计算(50,y),(-28,y)…就可以利用前面计算的数据,计算得出所求数据。在实际应用中,三次样条插值是最为实用的,但是学生时代,这部分内容只考察拉格朗日和牛顿,所以,你懂得。
给出几道题,作为练习。


A是一个函数集合,B是另外一个函数集合,a是A集合的一个子集,现在要在B集合找到一个函数使其最佳逼近a集合中的函数,这就是逼近。前面的最佳平方只是采取的衡量标准不同而已。数据拟合顾名思义,是一种趋势上的靠近,它不要求在每一个节点处都是给定的函数值(PS拉和牛都是在节点处无误差,只是他们的特点),只要尽可能接近给定值就可以了。但是多接近算接近呢,这就需要一个标准,这就是在每一个节点处所有节点的误差平方之和最小,则为最小二乘(再读一遍这个方法的名字,最小二乘:误差平方和的最小)。
数值积分的目的就是用被积函数的函数中的线性组合来近似定积分的值,这就为计算机计算积分提供了实现方法(Matlab便是如此)。若只是应对学校考试,只需记住概览图中n=1、2、4时的计算公式。还有一些积分(如反常积分)就可以采用高斯求积的公司来求取。数值微分同数值积分一样,用给定的函数离散数据来计算函数子啊某一点的微分值,也是便于计算机算法的实现。给出几个练习,如下:


对于求解非线性方程的根,如概览图所示,一般采用二分法或迭代法。二分法计算简单,但耗时巨大,迭代法就很好的避免这个问题,二分法需要20步计算的,迭代法5步就搞定,这就是优势,也是算法的意义所在。考试时,必须知道收敛阶(收敛速度)的证明,收敛性的证明。(PS:收敛性是证明该迭代方程是否收敛,收敛阶是收敛的速度怎样,越大越快)。给出练习,如下:

之所以把非线性方程的求解和线性方程的求解放在一起,在于都是使用迭代法,一脉相承,便于学习。在线性方程组的求解中,什么样的解才是最接近真值得呢?这里就需要一个标准,就像衡量两点之间的距离用绝对值一样,这里是线性方程组,也就是矩阵,那么衡量标准是什么呢?—-范数。由此便开始了求解线性方程组的旅程。知道并且能够写出雅克比和高斯—塞德尔的迭代格式和迭代方程,还有就是误差,前面提过,真值存在,但是求不出来,所以误差必然存在。明白严格对角占优,可以快速判断迭代法是否收敛。给出练习,如下:
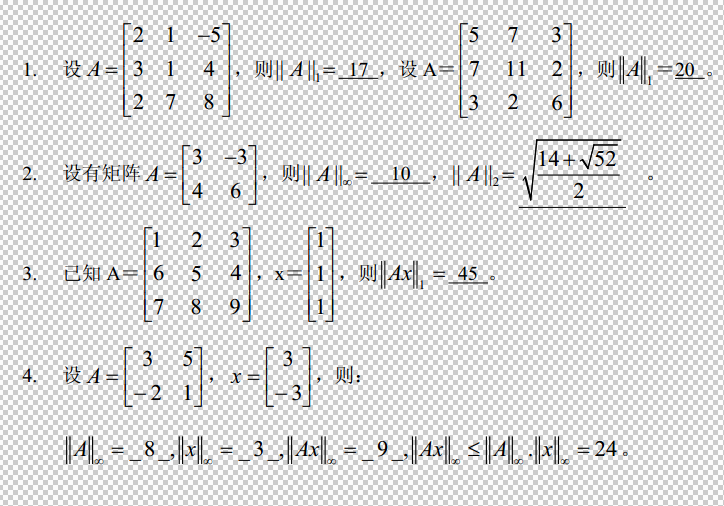
线性方程组也可直接求解,方法如概览图所示。针对5X5以下的矩阵,可以按照分解方法设出未知数,再按照矩阵运算规则解出未知数即完成分解(PS:针对学校考试,多为3X3的矩阵,所以设未知数比记住分解公式更快更简单,公式的推导只是为了计算机编程实现,手工计算不必如此)。给出练习,如下:

常微分方程这里只针对一阶,高阶微分方程有专门的学科讲授,在此不赘述。把欧拉法和改进欧拉法结合在一起,就是预估-校正法。由于欧拉法计算出的Yi+1误差较大,但是比自己任意给定的值效果要好,故把欧拉法计算的结果带入改进欧拉法中,就是预估校正了,欧拉法就是预估,改进欧拉法即为校正。给出练习,如下:


至此,简要的把数值分析梳理了一下,这只是简单的介绍,要深入学习数值分析,笔者建议没事多玩玩Matlab,自己试着把数值分析上面学到的算法编成代码,运行一下,看看运算的结果和MatLab自带的函数运算结果是否一致,精度如何,这也是数值分析用于实际的必由之路。数值分析,是算法的理论。
2016.01.18
chiefrr
























 1989
1989

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








