L3-023 计算图（分数80，C++）

“计算图”（computational graph）是现代深度学习系统的基础执行引擎，提供了一种表示任意数学表达式的方法，例如用有向无环图表示的神经网络。 图中的节点表示基本操作或输入变量，边表示节点之间的中间值的依赖性。 例如，下图就是一个函数
f(x1​,x2​)=lnx1​+x1​x2​−sinx2​
的计算图。

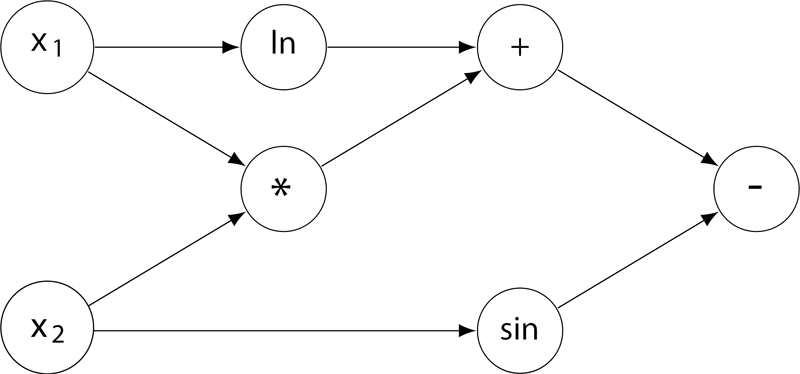
现在给定一个计算图，请你根据所有输入变量计算函数值及其偏导数（即梯度）。 例如，给定输入x1​=2,x2​=5，上述计算图获得函数值 f(2,5)=ln(2)+2×5−sin(5)=11.652；并且根据微分链式法则，上图得到的梯度 ∇f=[∂f/∂x1​,∂f/∂x2​]=[1/x1​+x2​,x1​−cosx2​]=[5.500,1.716]。

知道你已经把微积分忘了，所以这里只要求你处理几个简单的算子：加法、减法、乘法、指数（ex，即编程语言中的 exp(x) 函数）、对数（lnx，即编程语言中的 log(x) 函数）和正弦函数（sinx，即编程语言中的 sin(x) 函数）。

友情提醒：

• 常数的导数是 0；x 的导数是 1；ex 的导数还是 ex；lnx 的导数是 1/x；sinx 的导数是 cosx。
• 回顾一下什么是偏导数：在数学中，一个多变量的函数的偏导数，就是它关于其中一个变量的导数而保持其他变量恒定。在上面的例子中，当我们对 x1​ 求偏导数 ∂f/∂x1​ 时，就将 x2​ 当成常数，所以得到 lnx1​ 的导数是 1/x1​，x1​x2​ 的导数是 x2​，sinx2​ 的导数是 0。
• 回顾一下链式法则：复合函数的导数是构成复合这有限个函数在相应点的导数的乘积，即若有 u=f(y)，y=g(x)，则 du/dx=du/dy⋅dy/dx。例如对 sin(lnx) 求导，就得到 cos(lnx)⋅(1/x)。

如果你注意观察，可以发现在计算图中，计算函数值是一个从左向右进行的计算，而计算偏导数则正好相反。

输入格式：

输入在第一行给出正整数 N（≤5×104），为计算图中的顶点数。

以下 N 行，第 i 行给出第 i 个顶点的信息，其中 i=0,1,⋯,N−1。第一个值是顶点的类型编号，分别为：

• 0 代表输入变量
• 1 代表加法，对应 x1​+x2​
• 2 代表减法，对应 x1​−x2​
• 3 代表乘法，对应 x1​×x2​
• 4 代表指数，对应 ex
• 5 代表对数，对应 lnx
• 6 代表正弦函数，对应 sinx

对于输入变量，后面会跟它的双精度浮点数值；对于单目算子，后面会跟它对应的单个变量的顶点编号（编号从 0 开始）；对于双目算子，后面会跟它对应两个变量的顶点编号。

题目保证只有一个输出顶点（即没有出边的顶点，例如上图最右边的 -），且计算过程不会超过双精度浮点数的计算精度范围。

输出格式：

首先在第一行输出给定计算图的函数值。在第二行顺序输出函数对于每个变量的偏导数的值，其间以一个空格分隔，行首尾不得有多余空格。偏导数的输出顺序与输入变量的出现顺序相同。输出小数点后 3 位。

输入样例：

7
0 2.0
0 5.0
5 0
3 0 1
6 1
1 2 3
2 5 4

输出样例：

11.652
5.500 1.716

代码：

#include <iostream>
#include <cmath>

using namespace std;

const int N = 5e4 + 10;

int n, cnt = 1, root;
int ha[N]; // 数字存在标记数组
struct node {
    bool flag_calu; // 标记值是否已经计算过
    int x_num; // 如果是 x 值，记录它的位置
    int op; // 操作类型
    int back1, back2; // 二元操作的后续指针
    int front1, front2; // 前向指针（在这段代码中没有使用）
    double value; // 计算结果
}nodes[N];

// 计算节点值的函数
double calu(int num) {
    int op = nodes[num].op;
    int b1 = nodes[num].back1, b2 = nodes[num].back2;
    if (nodes[num].flag_calu) return nodes[num].value; // 如果值已经计算过，直接返回
    if (op == 0) {
        return nodes[num].value; // 如果是 x 值，直接返回
    } else if (op == 1) {
        return calu(b1) + calu(b2); // 加法
    } else if (op == 2) {
        return calu(b1) - calu(b2); // 减法
    } else if (op == 3) {
        return calu(b1) * calu(b2); // 乘法
    } else if (op == 4) {
        return exp(calu(b1)); // 指数函数
    } else if (op == 5) {
        return log(calu(b1)); // 自然对数
    } else if (op == 6) {
        return sin(calu(b1)); // 正弦函数
    }
}

// 计算关于 x 的导数
double dx(int num, int x) {
    int op = nodes[num].op;
    int b1 = nodes[num].back1, b2 = nodes[num].back2;
    if (op == 0) {
        return (nodes[num].x_num == x) ? 1.0 : 0.0; // 如果是 x 值，返回 1 或 0
    } else if (op == 1) {
        return dx(b1, x) + dx(b2, x); // 加法的导数
    } else if (op == 2) {
        return dx(b1, x) - dx(b2, x); // 减法的导数
    } else if (op == 3) {
        return dx(b1, x) * nodes[b2].value + dx(b2, x) * nodes[b1].value; // 乘法的导数
    } else if (op == 4) {
        return dx(b1, x) * nodes[num].value; // 指数函数的导数
    } else if (op == 5) {
        return 1.0 / nodes[b1].value * dx(b1, x); // 对数的链式法则
    } else if (op == 6) {
        return cos(nodes[b1].value) * dx(b1, x); // 正弦函数的导数
    }
}

int main() {
    cin >> n; // 操作的数量
    for (int i = 0; i < n; i ++ ) {
        int op, a, b;
        cin >> op; // 操作类型
        nodes[i].op = op;
        if (op == 0) {
            cin >> nodes[i].value;
            nodes[i].x_num = cnt ++; // 给 x 值分配位置
        } else if (op <= 3) {
            cin >> a >> b;
            ha[a] = ha[b] = 1; // 标记已使用的数字
            nodes[i].back1 = a, nodes[i].back2 = b; // 给二元操作分配后续指针
        } else {
            cin >> nodes[i].back1;
            ha[nodes[i].back1] = 1; // 标记已使用的数字
        }
    }
    // 寻找根节点
    for (int i = 0; i < n; i ++ ) if (!ha[i]) root = i, nodes[i].flag_calu = false;
    // 计算节点的值
    for (int i = 0; i < n; i ++ ) nodes[i].value = calu(i), nodes[i].flag_calu = true;
    printf("%.3lf\n", nodes[root].value); // 打印根节点的值
    // 打印导数
    for (int i = 1; i < cnt; i ++ ) {
        if (i == 1) printf("%.3lf", dx(root, i)); // 第一个导数
        else printf(" %.3lf", dx(root, i)); // 后续导数
    }
}

整活版

#include<iostream>
#include<cmath>
#define r(i) if(o==i)return
#define w for(int i=0;i<n;i++)
using namespace std;
int n,e=1,t,h[50010];struct node{bool f;int x_z,o,a,b;double v;}y[50010];
double c(int z){int o=y[z].o,a=y[z].a,b=y[z].b;if(y[z].f)return y[z].v;r(0)y[z].v;r(1)c(a)+c(b);r(2)c(a)-c(b);r(3)c(a)*c(b);r(4)exp(c(a));r(5)log(c(a));r(6)sin(c(a));}
double d(int z,int x){int o=y[z].o,a=y[z].a,b=y[z].b;r(0)y[z].x_z==x?1.0:0.0;r(1)d(a,x)+d(b,x);r(2)d(a,x)-d(b,x);r(3)d(a,x)*y[b].v+d(b,x)*y[a].v;r(4)d(a,x)*y[z].v;r(5)1.0/y[a].v*d(a,x);r(6)cos(y[a].v)*d(a,x);}
int main(){cin>>n;w {cin>>y[i].o;if(!y[i].o)cin>>y[i].v, y[i].x_z=e++;else if(y[i].o<=3)cin>>y[i].a>>y[i].b,h[y[i].a]=h[y[i].b]=1;else cin>>y[i].a,h[y[i].a]=1;}w if(!h[i])t=i;w y[i].v=c(i),y[i].f=true;printf("%.3lf\n%.3lf",y[t].v,d(t,1));for(int i=2;i<e;i++)printf(" %.3lf",d(t,i));}