代码：小波包分解与重构、小波包能量特征提取

1、小波变换的理解

傅里叶变换——短时傅里叶变换——小波变换。

参考文献：以下两篇参考资料讲述得十分清楚，有助于理解小波变换。

但具体的数学角度阐述，请参考其他资料。

（1）知乎专栏：形象易懂讲解算法I——小波变换

https://zhuanlan.zhihu.com/p/22450818

（2）知乎专栏：傅里叶分析之掐死教程。

https://zhuanlan.zhihu.com/p/19763358

2、小波包分解

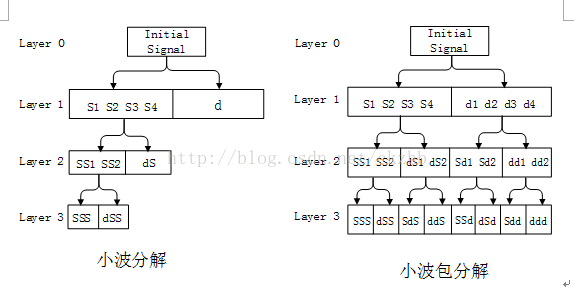
小波包是为了克服小波分解在高频段的频率分辨率较差，而在低频段的时间分辨率较差的问题的基础上而提出的。

它是一种更精细的信号分析的方法，提高了信号的时域分辨率。

下面是两者的对比图：

3、能量谱

      基于小波包分解提取多尺度空间能量特征的原理是把不同分解尺度上的信号能量求解出来，将这些能量值按尺度顺序排列成特征向量供识别使用。

20180510补充更新：具体计算公式如下所示，本文中未使用重构后的系数进行能量值计算，直接使用小波包分解后的系数，参考文献《基于小波包能量特征的滚动轴承故障监测方法 》。

4、Matlab代码

给出两部分代码，写成两个函数。一个是小波包分解与重构，另一个是能量谱函数。

下载地址：https://download.csdn.net/download/ckzhb/10030651

代码名称：wavelet_packetdecomposition_reconstruct

function wpt= wavelet_packetdecomposition_reconstruct( x,n,wpname )
%% 对信号进行小波包分解，得到节点的小波包系数。然后对每个节点系数进行重构。 
% Decompose x at depth n with wpname wavelet packets.using Shannon entropy.
%   
%  x-input signal,列向量。
%  n-the number of decomposition layers
%  wpname-a particular wavelet.type:string.
%
%Author hubery_zhang
%Date 20170714

%%
wpt=wpdec(x,n,wpname);
% Plot wavelet packet tree (binary tree)
plot(wpt)
%% wavelet packet coefficients.default：use the front 4.
cfs0=wpcoef(wpt,[n 0]);
cfs1=wpcoef(wpt,[n 1]);
cfs2=wpcoef(wpt,[n 2]);
cfs3=wpcoef(wpt,[n 3]);
figure;
subplot(5,1,1);
plot(x);
title('原始信号');
subplot(5,1,2);
plot(cfs0);
title(['结点 ',num2str(n) '  1',' 系数'])
subplot(5,1,3);
plot(cfs1);
title(['结点 ',num2str(n) '  2',' 系数'])
subplot(5,1,4);
plot(cfs2);
title(['结点 ',num2str(n) '  3',' 系数'])
subplot(5,1,5);
plot(cfs3);
title(['结点 ',num2str(n) '  4',' 系数'])
%% reconstruct wavelet packet coefficients.
rex0=wprcoef(wpt,[n 0]);
rex1=wprcoef(wpt,[n 1]);
rex2=wprcoef(wpt,[n 2]);
rex3=wprcoef(wpt,[n 3]);
figure;
subplot(5,1,1);
plot(x);
title('原始信号');
subplot(5,1,2);
plot(rex0);
title(['重构结点 ',num2str(n) '  1',' 系数'])
subplot(5,1,3);
plot(rex1);
title(['重构结点 ',num2str(n) '  2',' 系数'])
subplot(5,1,4);
plot(rex2);
title(['重构结点 ',num2str(n) '  3',' 系数'])
subplot(5,1,5);
plot(rex3);
title(['重构结点 ',num2str(n) '  4',' 系数'])
end

代码名称：wavelet_energy_spectrum

function E = wavelet_energy_spectrum( wpt,n )
%% 计算每一层每一个节点的能量
%  wpt-wavelet packet tree
%  n-第n层能量
% 
% Author hubery_zhang
% Date  20170714

%%
% 求第n层第i个节点的系数
E(1:2^n )=0;
for i=1:2^n 
E(i) = norm(wpcoef(wpt,[n,i-1]),2)^2; %20180604更新 原代码：E(i) = norm(wpcoef(wpt,[n,i-1]),2)
end
%求每个节点的概率
E_total=sum(E); 
for i=1:2^n
p_node(i)= 100*E(i)/E_total;
end
% E = wenergy(wpt); only get the last layer
figure;
x=1:2^n;
bar(x,p_node);
title(['第',num2str(n),'层']);
axis([0 2^n 0 100]);
xlabel('结点');
ylabel('能量百分比/%');
for j=1:2^n
text(x(j),p_node(i),num2str(p_node(j),'%0.2f'),...
    'HorizontalAlignment','center',...
    'VerticalAlignment','bottom')
end

end