数据可视化技巧-CSDN博客

本文链接：https://blog.csdn.net/cl2227619761/article/details/76383409

基本方法

在导入和清理数据之后，下一步通常就是逐一探索每个变量了。这就为你提供每个变量分布的信息，对理解样本的特征，识别意外的或有问题的值，以及选择合适的统计方法都是有帮助的。接下来是每次研究变量中的两个变量。这可以揭示变量间的基本关系，并且对于建立更复杂的模型来说是有益的第一步。
第二部分关注的是用于获取数据基本信息的图形技术和统计方法。第六章描述了可视化单个变量分布的方法。对于类别型变量，有条形图、饼图以及比较新的扇形图。对于数值型变量，有直方图、密度图、箱线图、点图和不那么著名的小提琴图。每类图形对于理解单个变量的分布都是有益的。第7章描述了用于概述单变量和双变量间关系的统计方法。这一章使用了一个完整的数据集，以数值型数据的描述性统计分析开始，研究了感兴趣的子集，接下来，它描述了用于概述类别型数据的频数分布表和列联表。这一章以对用于理解两个变量之间关系的方法进行讨论作结尾，包括二元相关关系的探索、卡方检验、t检验和非参数方法。在读完这一部分之后，你将能够使用R中的基本图形和统计方法来描述数据、探索组间差异，并识别变量间显著的关系。

基本图形

我们无论何时分析数据，第一件要做的事情就是观察它。对于每个变量，哪些值是最常见的？值域是大是小？是否有不寻常的观测？R中提供了丰富的数据可视化函数。本章，我们将关注那些可以帮助理解单个类别型或连续型变量的图形。主题包括：

将变量的分布进行可视化展示；
通过结果变量进行跨组比较

在以上话题中，变量可为连续型或类别型。在后续各章中，我们将探索那些展示双变量和多变量间关系的图形，在接下来的几节中，我们将探索条形图、饼图、扇形图、直方图、核密度图、箱线图、小提琴图和点图的用法。有些图形你可能已经很熟悉了，而有些图形（如扇形图或小提琴图）则可能比较陌生

条形图

条形图通过垂直的或水平的条形展示了类别型变量的分布（频数），函数barplot()的最简单用法是：barplot(height)其中的height是一个向量或矩阵，在接下来的示例中，我们将绘制一项探索类风湿性关节炎新疗法研究的结果。数据已包含在随vcd包分发的Arthritis数据框中。

简单的条形图

若height是一个向量，则它的值就确定了各条形的高度，并将绘制一副垂直的条形图。使用选项horiz=TRUE则会生成一副水平条形图。你也可以添加标注选项。选项main可添加一个图形标题，而选项xlab和ylab则会分别添加x轴和y轴标签。

library(vcd)
head(Arthritis)

在关节炎研究中，变量Improved记录了病人的治疗结果。

(count <- table(Arthritis$Improved)) # 这里可以看到28位明显改善，
# 14位部分改善，42位没有改善

第7章将充分讨论table()函数提取各单元的计数的方法。然后使用一幅垂直的或水平的条形图来绘制变量count。

barplot(count, main = "Simple Bar Plot", 
        xlab = "Improvement", 
        ylab = "Frequency", 
        col = rgb(.6, .2, .3), 
        border = FALSE,
        space = .8)

barplot(count, main = "Horizontal Bar Plot", 
        xlab = "Frequency", 
        ylab = "Improvement", 
        horiz = TRUE, 
        col = rgb(.5, .3, .2),
        border = FALSE,
        space = .8)

如果所要绘制的类别变量是一个因子或有序型因子，就可以使用函数plot()快速创建一幅垂直条形图。由于Arthritis$Improved是一个因子，所以可以用plot()函数快速创建垂直条形图，无需使用table()函数将其表格化。

plot(Arthritis$Improved, main = "Simple Bar Plot", 
     xlab = "Improved", 
     ylab = "Frequency", 
     col = rgb(.4, .6, .3), 
     border = FALSE,
     space = .8)

plot(Arthritis$Improved, main = "Horizontal Bar Plot", 
     xlab = "Frequency", 
     ylab = "Improved", 
     horiz = TRUE, 
     border = FALSE,
     col = rgb(.5, .3, .6), 
     space = .8)

如果标签很长怎么办？在6.1.4节中，你将看到微调标签的方法，这样它们就不会重叠了。

堆砌条形图和分组条形图

如果height是一个矩阵而不是一个向量的话，则绘图结果将会是一幅堆砌条形图或分组条形图。若beside=FALSE(默认值)，则矩阵中的每一列都将生成图中的一个条形，各列中的值将给出堆砌的“子条”的高度。若beside=TRUE，则矩阵中的每一列都表示一个分组，各列中的值将是并列而不是堆砌。比如，治疗类型和改善情况列联表就不再是一个单独的向量了, 而是一个矩阵。这个时候使用barplot()函数对列联表进行绘制条形图，结果将是堆砌条形图或分组条形图。

(counts <- table(Arthritis$Improved, Arthritis$Treatment))

barplot(counts, space = .65, # 调节条形之间的间距，避免过度拥挤
        main = "Stacked Bar Plot", 
        xlab = "Treatment", 
        ylab = "Improvement", 
        col = c(rgb(.4, .3, .2), 
                rgb(.8, .3, .2), 
                rgb(.5, .7, .8)),
        border = FALSE,
        xlim = c(0, 4), # 调节x轴的最大值，避免条形过度拥挤
        ylim = c(0, 50),
        las = 1
        )
legend(3.5, 44, rownames(counts), # 坐标可以使用locator函数识别出来
       fill  = c(rgb(.4, .3, .2), 
                 rgb(.8, .3, .2), 
                 rgb(.5, .7, .8)), 
       cex = 0.8)

结果将是一幅堆砌条形图，我们可以使用col选项为绘制的条形添加颜色。参数legend.text为图例提供了各条形的标签（注意：仅在绘制的变量为一个矩阵的时候有用）

均值条形图

条形图并不一定要基于计数数据或频率数据。你可以使用数据整合函数并将结果传递给barplot()函数，来创建表示均值、中位数、标准差等的条形图，比如：使用R自带的数据，绘制平均文盲率的条形图。

options(digits = 3)
states <- data.frame(state.region, state.x77)
head(states)

(mean_illit <- aggregate(states$Illiteracy, 
                        by = list(state.region), # 计算各地区的文盲均数
                        FUN = mean))

(mean_illit <- mean_illit[order(mean_illit$x), ]) # 将文盲均数升序排列

barplot(mean_illit$x, 
        names.arg = mean_illit$Group.1, # 该选项是为了展示条图标签
        main = "Mean Illiteracy Rate", 
        ylab = "Rate", 
        col = rgb(.5, .4, .6),
        space = .65,
        border = FALSE,
        las = 1)

条形图的微调

有若干种方式可以对条形图的外观进行微调。比如，随着条数的增多，条形的标签可能开始重叠。你可以使用cex.names来减小字号，将其指定为小于1的值可以缩小标签的大小。可选的参数names.arg允许你指定一个字符向量作为条形的标签名。同样可以使用图形参数辅助调整文本间隔。例如下面为条形图搭配标签，先看正常情况下的条形图。

counts <- table(Arthritis$Improved)
barplot(counts, 
        main = "Treatment Outcome", 
        horiz = TRUE,
        col = rgb(.6, .3, .2),
        border = FALSE,
        space = .65,
        names.arg = c("None Improvement", 
                      "Some Improvement", 
                      "Marked Improvement"),
        las = 2)

发现标签显示不全，所以要对该条形图进行微调

opar <- par(no.readonly = TRUE) # 保存当前图形参数设置，便于后续恢复
par(mar = c(5, 8, 4, 2)) # 增大边界大小，默认是5,4,4,2
barplot(counts, main = "Treatment Outcome", 
        horiz = TRUE, 
        col = rgb(.7, .4, .5), 
        border = FALSE, 
        space = .65,
        names.arg = c("None Improvement", 
                      "Some Improvement", 
                      "Marked Improvement"),
        cex.names = .8, # 缩小条形标签的字号大小
        las = 2)
par(opar)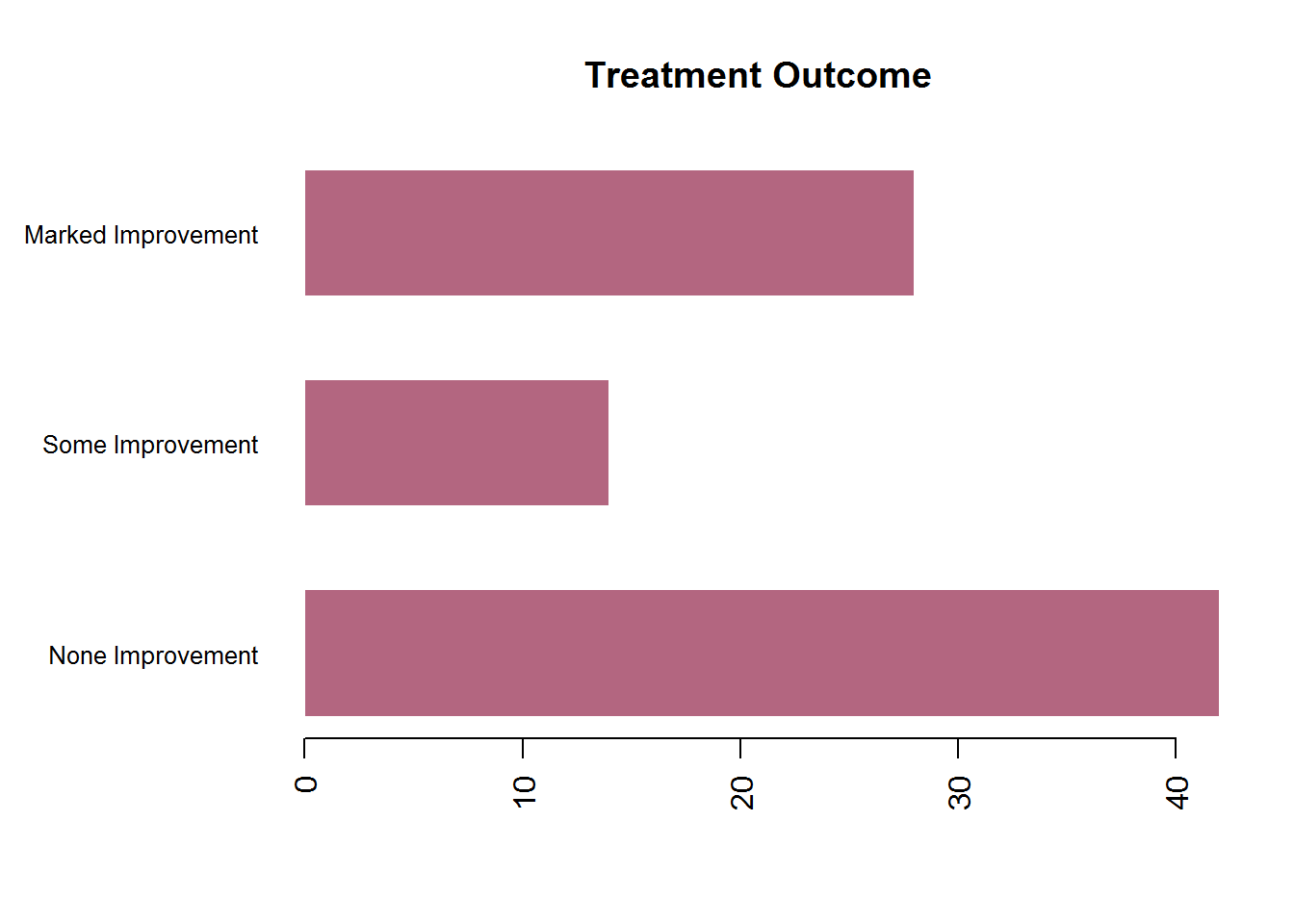

棘状图

在结束关于条形图的讨论之前，让我们再来看一种特殊的条形图，称为棘状图(spinogram)。棘状图对堆砌调图进行了重缩放，这样每个条形的高度均为1，每一段的高度表示比例，棘状图可由vcd包中的函数spine()绘制，下面对Arthritis数据集中的治疗类型和效果的列联表进行绘制。

(counts <- table(Arthritis$Treatment,
                Arthritis$Improved))

spine(counts, main = "Spinogram Example")

饼图

除了棘状图以外，饼图也是一种用于展示类别型变量分布的工具，饼图可由以下函数创建：pie(x, labels)
其中x是非负数值向量，表示每个扇形的面积，而labels则是表示各扇形标签的字符型向量。例：想要一幅由四幅图组成的图，其中第一幅为简单饼图，第二幅为带有百分比标签的饼图，第三幅为3D饼图，第四幅为美国不同地区州数组成的饼图。

opar <- par(no.readonly = TRUE)
par(mfrow = c(2, 2))
slice <- c(10, 12, 4, 16, 8)
lbles <- c("US", "UK", "Australia", "Germany", "France")
pie(slice, labels = lbles, 
    main = "Simple Pie Chart")

pct <- round(slice/sum(slice)*100)
lbles2 <- paste(lbles, " ", pct, "%", sep = "")
pie(slice, lbles2, col = rainbow(length(lbles2)), 
    main = "Pie Chart With Percentages")

library(plotrix)
pie3D(slice, labels = lbles, 
      explode = 0.1, 
      main = "3D Pie Chart")

(mytable <- table(state.region))
lbles3 <- paste(names(mytable), "\n", mytable, sep = "")
pie(mytable, labels = lbles3, 
    main = "Pie Chart from a Table\n (with sample sizes)")
par(opar)

饼图使得比较各扇形的值变得困难。为了改善这种情况，可以使用扇形图，提供了一种同时展示相对数量和相互差异的方法，在R中，扇形图是通过plotrix包中的fan.plot函数实现的。

library(plotrix)
slice <- c(10, 12, 4, 16, 8)
lbles <- c("US", "UK", "Australia", "Germany", "France")
fan.plot(slice, labels = lbles, 
         main = "Fan Plot")

直方图

直方图通过在x轴上将值域分割为一定数量的组，在y轴上显示相应的频数，展示了连续型变量的分布，可以使用如下函数创建直方图hist(x)。

其中x是一个由数据值组成的数值向量。参数freq=FALSE表示根据概率密度而不是频数绘制直方图。参数breaks用于控制组的数量。在定义直方图中的单元时，默认将生成等距切分。下面可以在一幅图中绘制四种不同的直方图进行对比。

opar <- par(no.readonly = TRUE)
par(mfrow = c(2, 2))

hist(mtcars$mpg) # 绘制一幅简单的直方图

hist(mtcars$mpg, 
     breaks = 12, # 将直方图的组数设为12组
     col = rgb(.9, .6, .5), # 设置颜色
     xlab = "Miles Per Gallon", # 设置x轴标签
     main = "Colored histogram with 12 breaks", # 设置直方图主标题 
     border = FALSE) # 去掉直方图边框

hist(mtcars$mpg, 
     freq = FALSE, # 绘制密度图，为添加核密度曲线做准备
     breaks = 12, 
     col = rgb(.9, .6, .5),
     border = FALSE,
     xlab = "Miles Per Gallon", 
     main = "Histogram, rug plot, density curve")
rug(jitter(mtcars$mpg)) # 添加轴须，轴须的目的是实际数据值的一种一维呈现方式
lines(density(mtcars$mpg), 
      col = rgb(.6, .3, .2), 
      lwd = 2) # 核密度曲线，目的是为数据的分布提供一种更平滑的描述

x <- mtcars$mpg
h <- hist(x, 
     breaks = 12, 
     xlab = "Miles Per Gallon", 
     border = FALSE,
     main = "Histogram with normal curve and box", 
     col = rgb(.9, .6, .5))
xfit <- seq(min(x), max(x), length.out = 40)
yfit <- dnorm(xfit, mean = mean(x), sd = sd(x))
yfit <- yfit*diff(h$mids[1:2])*length(x) 
# 在频数分布直方图上画正态分布曲线的一个计算公式
lines(xfit, yfit, col = "steelblue", lwd = 2)
box() # 给图加外框

par(opar)

核密度图

在上节中看到了直方图上叠加的核密度图。用术语来说，核密度曲线是用于估计随机变量概率密度函数的一种非参数方法。从总体上讲，核密度图是用来观察连续型变量分布的有效方法。绘制密度图的方法(不叠加到另一幅图上)为：
plot(density(x)) 其中x为一个数值型向量。由于plot()函数会创建一幅新的图形，所以要向一幅已经存在的图形上添加一条密度曲线，可以使用lines()函数

下面以mtcars数据集的mpg变量为例，观察mpg的分布，绘制mpg的概率密度曲线

opar <- par(no.readonly = TRUE)
par(mfrow = c(2, 1))

d <- density(mtcars$mpg)

plot(d) # 绘制使用默认设置的最简图形

plot(d, main = "Kernel Density of Miles Per Gallon") # 添加主标题
polygon(d, col = "red", border = "steelblue") # 绘制多边形
rug(mtcars$mpg, col = "brown") # 添加轴须图

par(opar)

核密度图可以用于比较组间差异。这种方法可以使用sm包实现

sm包中的sm.density.compare()函数可向图形叠加两组或更多的核密度图，格式为：sm.density.compare(x, factor)
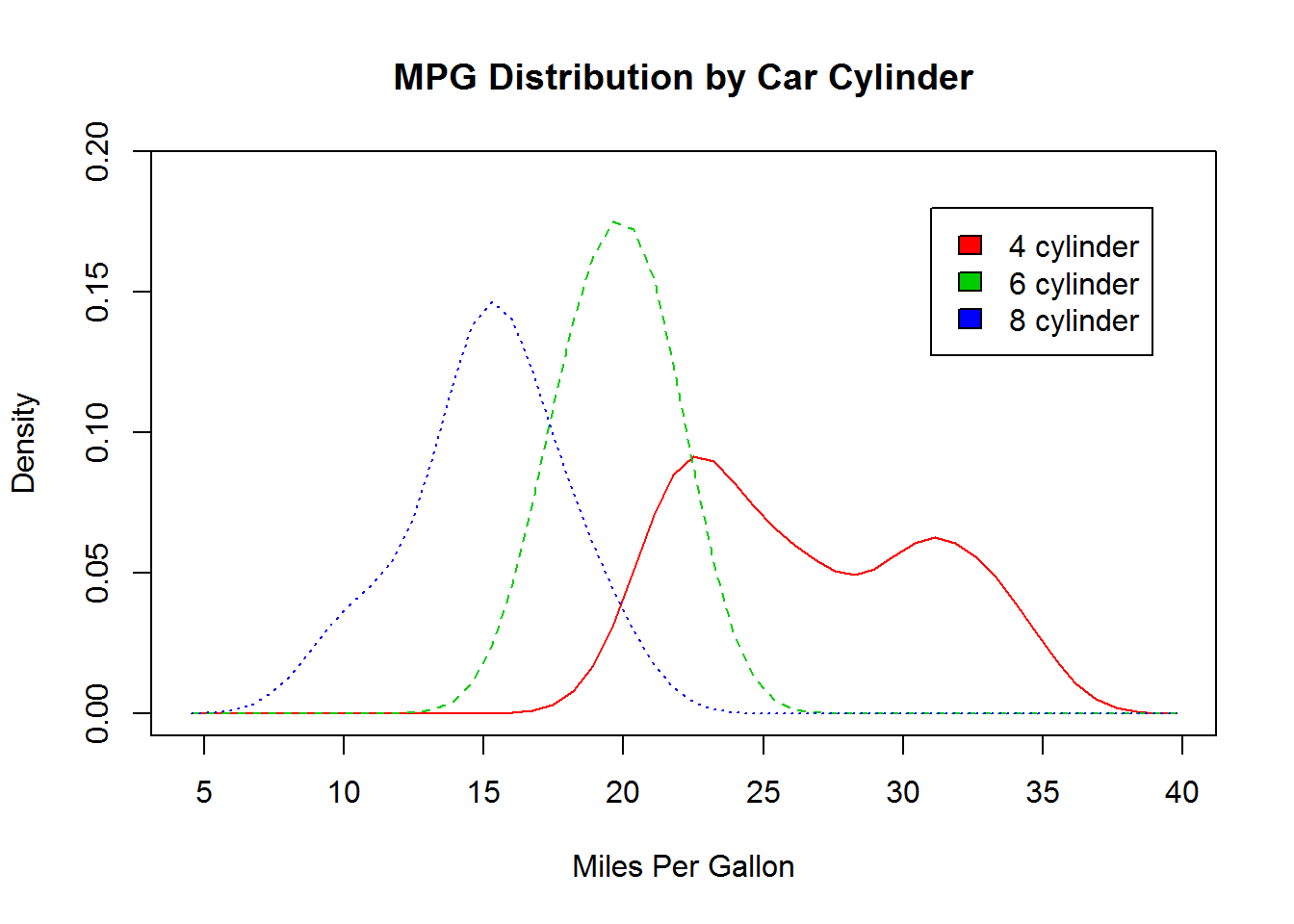
其中x是一个数值型向量，factor是一个分组变量。下面使用核密度图对拥有4个、6个或8个气缸车型的mpg进行比较

library(sm)
str(mtcars)

with(mtcars, {
  cyl.f <<- factor(cyl, levels = c(4, 6, 8), # cyl(气缸)为数值型，转化为分组因子
                   labels = c("4 cylinder", 
                              "6 cylinder",
                              "8 cylinder"))

  sm.density.compare(mpg, cyl.f, 
                     xlab = "Miles Per Gallon") # 绘制密度图

  title(main = "MPG Distribution by Car Cylinder")
  colfill <- c(2, 3, 4)

  legend(31, .18, levels(cyl.f), fill = colfill) # 添加图例
})

箱线图

箱线图通过绘制连续型变量的五数总括，即最小值、下四分位数、中位数、上四分位数和最大值，描述了连续型变量的分布。箱线图还能显示离群值(1.5倍IQR之外的观测)。

下面作出mtcars数据集中变量mpg的箱线图，观察变量mpg的分布。

boxplot(mtcars$mpg, 
        main = "Box plot", 
        ylab = "Miles Per Gallon", 
        col = rgb(.9, .4, .5), 
        las = 2)

结果显示上面的须稍微长一点，说明这些数据稍微正偏。

默认情况下，两条须的延伸极限不会超过盒型各端加1.5倍的IQR的范围，此范围以外的值将用点表示，为异常点。

可以使用boxplot.stats()函数查看用于构造箱线图的统计量。

boxplot.stats(mtcars$mpg)

可以看出最小值为10.4，下四分位数为15.35，中位数为19.20，上四分位数为22.80，最大值为33.9；观测数目为32；没有离群点。

关于boxplot.stats()函数，他的输出结果的意义是：我们就可以用boxplot.stats()函数来查看详细的信息，stats信息是去掉异常值的极值，四分位数，以及中位数，n的信息表示属性数据点的个数，conf的信息表示 $median\pm{\frac {1.5*INQ}{\sqrt{n}}}$ 的结果，是用来衡量中位数的一个置信区间，out的信息表示属性中异常值的具体数值。

并列箱线图

箱线图可以用于展示单个变量或分组变量，使用格式为：boxplot(formula, data = datafram)，其中formula是一个公式，dataframe代表提供数据的数据框或列表。比如：公式y\~A，表示为类别型变量A的每个值并列地生成数值型变量y的箱线图。公式y\~A*B，表示为类别型变量A和B所有水平的两两组合生成数值型变量y的箱线图。

参数varwidth=TRUE会使箱线图的宽度与其样本大小的平方根成正比。参数horiz=TRUE反转坐标轴

下面使用并列箱线图对比四缸、六缸和八缸发动机对mpg的影响。首先要明白这里的数值型变量为mpg，分组变量为发动机缸数cyl。

boxplot(mpg ~ cyl, data = mtcars,
        main = "Car Mileage Data", 
        xlab = "Number of Cylinders", 
        ylab = "Miles Per Gallon", 
        col = c(rgb(.3, .6, .4), 
                rgb(.8, .4, .2), 
                rgb(.9, .5, .6)))
legend(2.8, 34.3, paste0(c(4, 6, 8), "cylinders", " "),
       fill = c(rgb(.3, .6, .4), 
                rgb(.8, .4, .2), 
                rgb(.9, .5, .6)))
cyl.mean <- aggregate(mtcars$mpg,
                   by = list(mtcars$cyl), 
                   FUN = mean)$x
abline(h=cyl.mean, # 添加均值辅助线
       lty = 1, 
       col = "blue")

数据分析：

不同气缸车型之间的每加仑英里数区别非常明显；
与4缸和8缸相比，6缸的每加仑英里数据分布较为均匀。4缸的每加仑英里数分布最广，并且正偏(上方的触须大于下方)。8缸的还有个离群点。(要我选的话我会选择4缸的，哈哈)。这个箱线图可以和叠加的核密度图放到一起作比较。

library(sm)
cyl.f <- factor(mtcars$cyl, 
                   levels = c(4, 6, 8), 
                   labels = c("4 cylinder", 
                              "6 cylinder", 
                              "8 cylinder"))
sm.density.compare(mtcars$mpg, cyl.f, 
                   main = "Car Mileage Data", 
                   xlab = "Miles Per Gallon")
legend(31, .18, levels(cyl.f), 
       fill = c(2, 3, 4))
abline(v = cyl.mean, 
       lty = 2, 
       col = "black")# 添加均值辅助线

箱线图还可以加上凹槽，通过设置notch=TRUE。若两个箱线图的凹槽互不重叠，说明他们的中位数有显著性差异。

boxplot(mpg ~ cyl, data = mtcars,
        notch = TRUE, 
        varwidth = TRUE, # 使箱宽和各自样本量成正比
        main = "Car Mileage Data", 
        xlab = "Number of Cylinders", 
        ylab = "Miles Per Gallon", 
        col = c(rgb(.3, .6, .4), 
                rgb(.8, .4, .2), 
                rgb(.9, .5, .6)))
legend(2.8, 34.3, 
       c("4 cylinder", 
         "6 cylinder", 
         "8 cylinder"), 
       fill = c(rgb(.3, .6, .4), 
                rgb(.8, .4, .2), 
                rgb(.9, .5, .6)))

数据分析：

三组的mpg中位数是不一样的；
随着气缸数的减少，油耗相应减少。

除了对一个按分组因子绘制并列箱线图，还可以设置多个分组因子，绘制交叉因子的箱线图，格式为：y\~A*B，下面将气缸数cyl和变速箱的类型am作为分组因子来绘制mpg的箱线图。自然，这里的数值变量为mpg，分组变量为cyl和am。

with(mtcars, {
  str(cyl)
  str(am)
}) # 二者都是数值型，故需要转为factor

with(mtcars, {
  cyl.f <<- factor(cyl, 
                   levels = c(4, 6, 8),
                   labels = c("4", "6", "8"))
  am.f <<- factor(am, 
                  levels = c(0, 1), 
                  labels = c("auto",
                             "standard"))
})
boxplot(mpg ~ am.f * cyl.f, 
        data = mtcars, 
        main = "MPG distribution by Auto Type", 
        xlab = "Auto Type", 
        ylab = "Miles Per Gallon", 
        col = c("gold", "darkgreen"), 
        varwidth = TRUE)

数据分析：

随着气缸数目的减少，油耗减少；
对于4缸和6缸来说，standard变速箱油耗少，而8缸则没有区别；
从宽度可以看出standard.4和auto.8在数据集中更常见。

小提琴图

小提琴图是箱线图和核密度图的结合体。箱线图展示的是数据分位数的位置；核密度图展示的是数据在任意位置的密度。将二者结合的小提琴图可以很好的展现数据的分布情况。

绘制小提琴图的函数为vioplot包中的vioplot()，格式为：
vioplot(x1, x2, ... , names=, col=)，其中x为要绘制的一个或多个数值向量，names=是小提琴中的标签。

library(vioplot)
x1 <- mtcars$mpg[mtcars$cyl == 4]
x2 <- mtcars$mpg[mtcars$cyl == 6]
x3 <- subset(mtcars, cyl == 8, 
             select = mpg) # 主要为了复习一下subset函数
vioplot(x1, x2, x3$mpg, 
        names = c("4 cyl", 
                  "6 cyl", 
                  "8 cyl"), 
        col = "gold")
title("Violin plot of MPG", 
      xlab = "Number of cylinders", 
      ylab = "Miles Per Gallon")

图形解释：

白点是中位数，黑色箱体标注上下四分位数
细黑线表示须
外部轮廓表示核密度估计，展示任意位置的密度

数据分析：

油耗随着气缸数目的减少而减少
4缸油耗分布分散，6缸油耗分布集中，8缸油耗分布很不均匀(密度中间大两头小)
4缸和8缸可能存在离群值，因为4缸上侧须长于下侧(正偏，有极大值)，8缸下侧长(有极小值)

点图

点图可以实现在水平刻度上绘制大量标签值，格式为：dotchart(x, labels=)，其中x是数值向量，labels是由每个点的标签组成的向量。groups参数可以选定一个因子，指定x中元素的分组方式，gcolor控制不同组标签的颜色；cex控制标签的大小。下面以mtcars数据集为例，数值向量为mpg，那么mpg将作为水平刻度，简单绘制点图

dotchart(mtcars$mpg, # x轴的内容
         labels = rownames(mtcars), # y轴内容
         cex = .7,
         main = "Gas Mileage for Car Models", 
         xlab = "Miles Per Gallon")

可以发现，这样的点图好像没有太大的意义，但是如果将数值向量按照某个因子进行分组，并排序，再赋予不同的形状和颜色，那么点图的意义就很好的体现出来了。

x <- mtcars[order(mtcars$mpg), ] # 对mtcars数据集按mpg升序排列
x$cyl <- factor(x$cyl) # 将cyl转变为因子型
x$color[x$cyl == 4] <- "red"
x$color[x$cyl == 6] <- "blue"
x$color[x$cyl == 8] <- "darkgreen"
dotchart(x$mpg, 
         labels = row.names(x), 
         cex = .65,
         groups = x$cyl, # 按照cyl分组
         gcolor = "black", # 组别的颜色
         color = x$color, # 点和标签的颜色
         pch = 19, 
         main = "Gas Mileage for Car Models\ngrouped by cylinder",
         xlab = "Miles Per Gallon")