poj 1066 Treasure Hunt （线段相交判定）

Treasure Hunt Time Limit: 1000MS   Memory Limit: 10000K Total Submissions: 6767   Accepted: 2807 Description Archeologists from the Antiquities and Curios Museum (ACM) have flown to Egypt to examine the great pyramid of Key-Ops. Using state-of-the-art technology they are able to determine that the lower floor of the pyramid is constructed from a series of straightline walls, which intersect to form numerous enclosed chambers. Currently, no doors exist to allow access to any chamber. This state-of-the-art technology has also pinpointed the location of the treasure room. What these dedicated (and greedy) archeologists want to do is blast doors through the walls to get to the treasure room. However, to minimize the damage to the artwork in the intervening chambers (and stay under their government grant for dynamite) they want to blast through the minimum number of doors. For structural integrity purposes, doors should only be blasted at the midpoint of the wall of the room being entered. You are to write a program which determines this minimum number of doors.  An example is shown below: 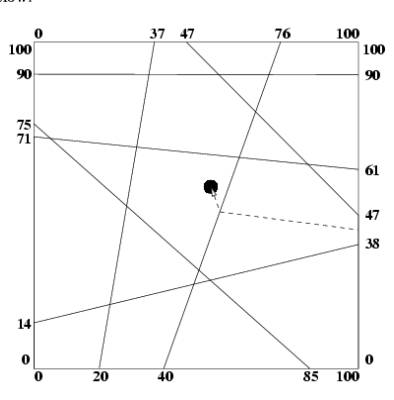 Input The input will consist of one case. The first line will be an integer n (0 <= n <= 30) specifying number of interior walls, followed by n lines containing integer endpoints of each wall x1 y1 x2 y2 . The 4 enclosing walls of the pyramid have fixed endpoints at (0,0); (0,100); (100,100) and (100,0) and are not included in the list of walls. The interior walls always span from one exterior wall to another exterior wall and are arranged such that no more than two walls intersect at any point. You may assume that no two given walls coincide. After the listing of the interior walls there will be one final line containing the floating point coordinates of the treasure in the treasure room (guaranteed not to lie on a wall). Output Print a single line listing the minimum number of doors which need to be created, in the format shown below. Sample Input 7 20 0 37 100 40 0 76 100 85 0 0 75 100 90 0 90 0 71 100 61 0 14 100 38 100 47 47 100 54.5 55.4 Sample Output Number of doors = 2 Source East Central North America 1999

[Submit]   [Go Back]   [Status]   [Discuss]

题目大意：在一个正方形中，有若干条端点在正方形边界的线段。给定正方形中一点，求从该点到正方形外部需要最少穿越的线段数量。注意除边界外，其他线段只能从线段的中点穿过。

题解：线段相交判断

因为端点都在正方形的边界，所以只要起点与终点的连线与该线段相交，那么我们如果选择这条线路的话，必然需要经过这条线段的中点，因为端点都在边界上，所以必然无法绕路。

我们枚举边界上的端点，求所有端点与给出的点的连线与其他线段的最少交点数。因为边界也需要穿过，所有ans+1.

线段规范相交的充要条件是：每条线段的两个端点都在另一个条线段的两侧（这里的两侧是指叉积的符号不同）

#include<iostream>
#include<cstring>
#include<cstdio>
#include<algorithm>
#include<cmath>
#define N 103
#define eps 1e-7
using namespace std;
struct vector 
{
	double x,y;
	vector (double X=0,double Y=0)
	{
		x=X,y=Y;
	}
};
vector operator -(vector a,vector b) {
	return vector(a.x-b.x,a.y-b.y);
}
int n,num;
typedef vector point;
point a[N],b[N],tmp,door[N];
int dcmp(double x)
{
	if (fabs(x)<eps) return 0;
	return x<0?-1:1;
}
double cross(vector a,vector b)
{
	return a.x*b.y-a.y*b.x;
}
int segmentpd(point a1,point a2,point b1,point b2)
{
	double c1=cross(a2-a1,b1-a1),c2=cross(a2-a1,b2-a1),
	       c3=cross(b2-b1,a1-b1),c4=cross(b2-b1,a2-b1);
	return dcmp(c1)*dcmp(c2)<0&&dcmp(c3)*dcmp(c4)<0;
}
int main()
{
   freopen("a.in","r",stdin);
   scanf("%d",&n);	
   for (int i=1;i<=n;i++){
    scanf("%lf%lf%lf%lf",&a[i].x,&a[i].y,&b[i].x,&b[i].y);
    door[++num]=a[i]; door[++num]=b[i];
   }
   scanf("%lf%lf",&tmp.x,&tmp.y);
   int ans=n;
   for (int i=1;i<=2*n;i++) {
   	  int t=0;
   	  for (int j=1;j<=n;j++){
       if (door[i].x==a[j].x&&door[i].y==a[j].y||door[i].x==b[j].x&&door[i].y==b[j].y) continue;
   	   t+=segmentpd(door[i],tmp,a[j],b[j]);
      }
   	  ans=min(ans,t);
   }
   if (n)  printf("Number of doors = %d\n",ans+1);
   else printf("Number of doors = 1\n");
}