转自 面试算法:格子取数问题,完美洗牌算法
http://www.aboutyun.com/thread-9995-1-1.html
(出处: about云开发)
题目详情:有n*n个格子,每个格子里有正数或者0,从最左上角往最右下角走,只能向下和向右,一共走两次(即从左上角走到右下角走两趟),把所有经过的格子的数加起来,求最大值SUM,且两次如果经过同一个格子,则最后总和SUM中该格子的计数只加一次。
题目分析:此题是去年2013年搜狗的校招笔试题。初看到此题,因为要让两次走下来的路径总和最大,读者可能最初想到的思路可能是让每一次的路径都是最优的,即不顾全局,只看局部,让第一次和第二次的路径都是最优。
但问题马上就来了,虽然这一算法保证了连续的两次走法都是最优的,但却不能保证总体最优,相应的反例也不难给出,请看下图:
上图中,图一是原始图,那么我们有以下两种走法可供我们选择:
- 如果按照上面的局部贪优走法,那么第一次势必会如图二那样走,导致的结果是第二次要么取到2,要么取到3,
- 但若不按照上面的局部贪优走法,那么第一次可以如图三那样走,从而第二次走的时候能取到2 4 4,很显然,这种走法求得的最终SUM值更大;
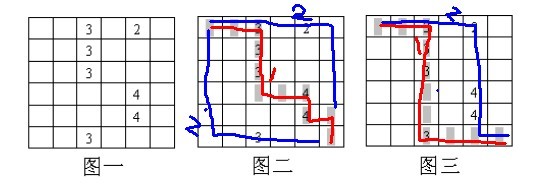
也就是说,上面图二中的走法太追求每一次最优,所以第一次最优,导致第二次将是很差;而图三第一次虽然不是最优,但保证了第二次不差,所以图三的结果优于图二。由此可知不要只顾局部而贪图一时最优,而丧失了全局最优。
解法一、直接搜索
局部贪优不行,我们可以考虑穷举,但最终将导致复杂度过高,所以咱们得另寻良策。
针对此题,可以使用直接搜索法,一共搜(2n-2)步,每一步有四种走法,考虑不相交等条件可以剪去很多枝,代码如下:
//copyright@西芹_new 2013
#include "stdafx.h"
#include <iostream>
using namespace std;
#define N 5
int map[5][5]={
{2,0,8,0,2},
{0,0,0,0,0},
{0,3,2,0,0},
{0,0,0,0,0},
{2,0,8,0,2}};
int sumMax=0;
int p1x=0;
int p1y=0;
int p2x=0;
int p2y=0;
int curMax=0;
void dfs( int index){
if( index == 2*N-2){
if( curMax>sumMax)
sumMax = curMax;
return;
}
if( !(p1x==0 && p1y==0) && !(p2x==N-1 && p2y==N-1))
{
if( p1x>= p2x && p1y >= p2y )
return;
}
//right right
if( p1x+1<N && p2x+1<N ){
p1x++;p2x++;
int sum = map[p1x][p1y]+map[p2x][p2y];
curMax += sum;
dfs(index+1);
curMax -= sum;
p1x--;p2x--;
}
//down down
if( p1y+1<N && p2y+1<N ){
p1y++;p2y++;
int sum = map[p1x][p1y]+map[p2x][p2y];
curMax += sum;
dfs(index+1);
curMax -= sum;
p1y--;p2y--;
}
//rd
if( p1x+1<N && p2y+1<N ) {
p1x++;p2y++;
int sum = map[p1x][p1y]+map[p2x][p2y];
curMax += sum;
dfs(index+1);
curMax -= sum;
p1x--;p2y--;
}
//dr
if( p1y+1<N && p2x+1<N ) {
p1y++;p2x++;
int sum = map[p1x][p1y]+map[p2x][p2y];
curMax += sum;
dfs(index+1);
curMax -= sum;
p1y--;p2x--;
}
}
int _tmain(int argc, _TCHAR* argv[])
{
curMax = map[0][0];
dfs(0);
cout <<sumMax-map[N-1][N-1]<<endl;
return 0;
}
解法二、动态规划
上述解法一的搜索解法是的时间复杂度是指数型的,如果是只走一次的话,是经典的dp。
2.1、DP思路详解 故正如@绿色夹克衫所说:此题也可以用动态规划求解,主要思路就是同时DP 2次所走的状态。
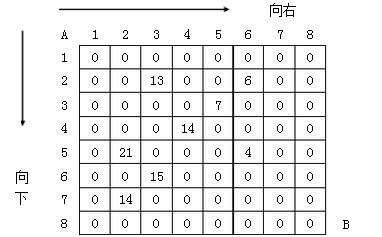
1、先来分析一下这个问题,为了方便讨论,先对矩阵做一个编号,且以5*5的矩阵为例(给这个矩阵起个名字叫M1):
M1
0 1 2 3 4
1 2 3 4 5
2 3 4 5 6
3 4 5 6 7
4 5 6 7 8
再来分析一下经过其他s步后所处的位置,根据上面的讨论,可以知道:
- 经过8步后,一定处于右下角(8);
- 那么经过5步后(s = 5),肯定会处于编号为5的位置;
- 3步后肯定处于编号为3的位置;
- s = 4的时候,处于编号为4的位置,此时对于方格中,共有5(相当于n)个不同的位置,也是所有编号中最多的。
如果用DP[s,i,j]来记录2次所走的状态获得的最大值,其中s表示走s步,i和j分别表示在s步后第1趟走的位置和第2趟走的位置。
2、为了方便描述,再对矩阵做一个编号(给这个矩阵起个名字叫M2):
0 0 0 0 0
1 1 1 1 1
2 2 2 2 2
3 3 3 3 3
4 4 4 4 4
我们先看M1,在经过6步后,肯定处于M1中编号为6的位置。而M1中共有3个编号为6的,它们分别对应M2中的2 3 4。故对于M2来说,假设第1次经过6步走到了M2中的2,第2次经过6步走到了M2中的4,DP[s,i,j] 则对应 DP[6,2,4]。由于s = 2n - 2,0 <= i<= <= j <= n,所以这个DP共有O(n^3)个状态。
再来分析一下状态转移,以DP[6,2,3]为例(就是上面M1中加粗的部分),可以到达DP[6,2,3]的状态包括DP[5,1,2],DP[5,1,3],DP[5,2,2],DP[5,2,3]。
因此:
DP[6,2,3] = Max(DP[5,1,2] ,DP[5,1,3],DP[5,2,2],DP[5,2,3]) + 6,2和6,3格子中对应的数值 (式一)
所以当i = j时,
DP[6,2,2] = Max(DP[5,1,1],DP[5,1,2],DP[5,2,2]) + 6,2格子中对应的数值 (式二)
复杂度分析:状态转移最多需要统计4个变量的情况,看做是O(1)的,共有O(n^3)个状态,所以总的时间复杂度是O(n^3)的,且dp数组开了N^3大小,故其空间复杂度亦为O(n^3)。
2.3、DP实现优化版
如上节末所说,2.2节实现的代码的复杂度空间复杂度是O(n^3),事实上,空间上可以利用滚动数组优化,由于每一步的递推只跟上1步的情况有关,因此可以循环利用数组,将空间复杂度降为O(n^2)。
即我们在推算dp[step]的时候,只依靠它上一次的状态dp[step - 1],所以dp数组的第一维,我们只开到2就可以了。即step为奇数时,我们用dp[1][j]表示状态,step为偶数我们用dp[0][j]表示状态,这样我们只需要O(n^2)的空间,这就是滚动数组的方法。滚动数组写起来并不复杂,只需要对上面的代码稍作修改即可,优化后的代码如下:
























 3778
3778

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








