HTML5实现一笔画游戏

HTML5实现一笔画游戏

一笔画问题

一笔画是图论科普中一个著名的问题，它起源于柯尼斯堡七桥问题科普。当时的东普鲁士哥尼斯堡城中有一条河，在这条河上有七座桥：

蓝色的代表河，这条河将城市分开成为四个区域，而七个橙色的矩形为座桥。

欧拉把实际的问题抽象为平面上的点与线，每一座桥视为一条线，桥所连接的地区视为点。

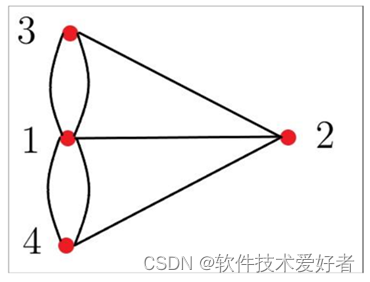
 “一笔画”问题涉及的核心概念包括连通图、奇点、偶点等。连通图指的是图中任意两个顶点之间都存在一条路径相连且没有重复。奇点则是与奇数个边相连的顶点，偶点则是与偶数个边相连的顶点。

欧拉发现，一个连通图能够一笔画出的条件是：要么图中所有顶点都是偶点，要么图中只有两个奇点。这个规律被称为欧拉定理，它为解决一笔画问题提供了理论基础。

由于哥尼斯堡七桥问题的抽象图中的四个顶点全部是奇顶点，所以它无法实现符合要求的走法，也就是不可能一笔画成。

数学家欧拉在他1736年发表的论文《柯尼斯堡的七桥》中不仅解决了七桥问题，也提出了一笔画定理，顺带解决了一笔画问题。他的这篇论文也成为图论史上第一篇重要文献。

HTML5实现一笔画游戏

HTML5和Canvas API提供了强大的图形处理能力，足以支持一笔画这样的游戏开发。

先给出效果图示：