【学习报告】10.17-10.23

优化算法

Mini-batch 梯度下降

1. 将X分割为若干个Mini-batch，用 { 大括号上标 } 来区分不同的batch，X^{t} ，Y^{t} ，J^{t}
2. 进行while循环训练，每一次迭代，都要遍历所有batch，每一个batch都进行一次W和B的调整，所以从效果上来说，曾经一次迭代只能调整一次W和B，现在可以调整若干次。
3. iteration和一个mini-batch对应，epoch(代数)和mini-batch的总体(也就是整个训练集)对应。

使用 batch 梯度下降法(就是之前的梯度下降)时，每次迭代你都需要历遍整个训练集，可以预期每次迭代成本
都会下降，所以如果成本函数J是迭代次数的一个函数，它应该会随着迭代而减少。

使用mini-batch梯度下降法，成本函数J^{t} 随迭代次数时而上升时而下降，但总体趋势是下降的。

需要考虑的变量就是mini-batch的大小，m就是训练集的大小：

当mini-batch的大小等于m时，就是batch梯度下降，所以就只有X^{1} Y^{1} ，也就是X Y。

当mini-batch的大小等于1时，叫做随机梯度下降，每一个样本就是一个mini-batch。缺点是从某一点开始，每次迭代，你只对一个样本进行梯度下降，大部分时候你向着全局最小值靠近，有时候你会远离最小值，因为那个样本恰好给你指的方向不对，因此随机梯度下降法是有很多噪声的，平均来看，它最终会靠近最小值，不过有时候也会方向错误，因为随机梯度下降法永远不会收敛，而是会一直在最小值附近波动，但它并不会在达到最小值并停留在此。而且每次迭代只要一个样本，失去了向量化带来的训练加速。

因此需要选择一个不是很大也不是很小的mini-batch。选择原则如下：

• 如果训练集比较小，直接使用batch梯度下降，这里少一般是指小于2000个样本
• 如果比较大，可以尝试一下64到512，把mini-batch大小设置为2的次方会使代码运行的快一些

稳定波动的算法

指数加权平均

思想：牺牲一点准确度来快速计算平均值

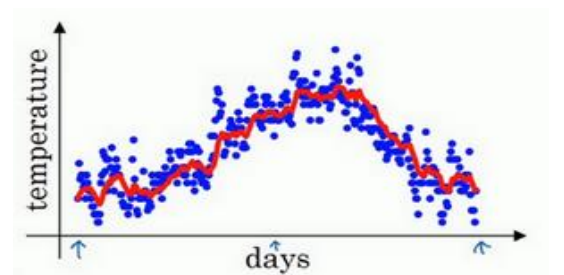
下图是一个关于每天的温度的散点图

如果要计算趋势的话，也就是温度的局部平均值，或者说移动平均值，我们要做的是[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-kzOJAc9e-1666575987476)(https://cdn.jsdelivr.net/gh/DaoChenLiu/images/learning_report3/202210232221663.png)]（θ_t 是当天的温度)

如果β等于0.9，大约是10天的平均值，用红线作图，如下所示：

如果β等于0.98，大约是50天的平均值，用绿线作图：

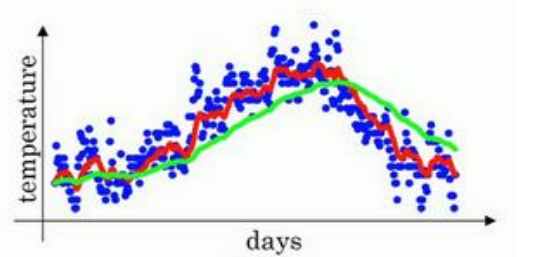
如果β等于0.5，大约是2天的平均值，用黄线作图：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-eR6W0Pd7-1666575987478)(https://cdn.jsdelivr.net/gh/DaoChenLiu/images/learning_report3/202210191039966.png)]

以上三种情况中，第一个图更能反映出趋势，因为它利用了适当的天数来求移动平均值。

因此我们可以得出结论,β越趋近于1，平均的样本就越多，曲线受当天的影响就越小，优点就是抗噪声，缺点就是呈现一种延迟（latency），对样本的适应性下降。

当β等于0.9时，0到100的平均如下：

如果把括号展开：

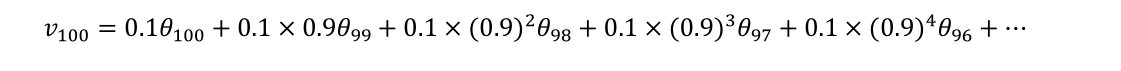
把这个公式分成两部分，一部分是每天的温度，每一部分是温度前面的系数

这些系数就构成了指数衰减函数，从0.1开始，到0.1×0.9，到0.1×0.9² ，以此类推。这些系数加起来为1或者逼近1，我们称之为偏差修正。

这两部分相乘然后相加就得到了某天的移动平均值。可以很明显看出来这个公式具有记忆效应，对越近的样本记忆效应越强（权重大），越远的样本，就会被越多的β \betaβ作用，权重不断减少

实际上在执行时，首先将v初始化为0，

第一天：v=βv + (1-β) θ₁ (θ₁ 是第一天的温度)

第二天：v=βv + (1-β) θ₂ (θ₂ 是第二天的温度)

…

指数加权平均数公式的好处之一在于，它占用极少内存，电脑内存中只占用一行数字而已，然后把最新数据代入公式，不断覆盖就可以了，正因为这个原因，其效率，它基本上只占用一行代码，计算指数加权平均数也只占用单行数字的存储和内存，当然它并不是最好的，也不是最精准的计算平均数的方法。如果你要计算移动窗，你直接算出过去 10 天的总和,过去 50 天的总和，除以 10 和 50 就好，如此往往会得到更好的估测。但缺点是，如果保存所有最近的温度数据，和过去 10 天的总和，必须占用更多的内存，执行更加复杂，计算成本也更加高昂。

偏差修正

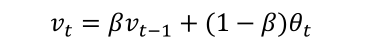
偏差修正的作用就是使得平均数更加的准确，特别是在训练早期，如果不进行修正的话，实际的平均数与真实值差别很大。

修正公式：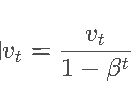

可以看出，t越小，修正程度越大，当t很大时，分母趋于1，相当于没有修正。

动量梯度下降法

实际上，无论是batch还是mini-batch，梯度下降的方向并不总是最好的方向，存在着非最优方向的波动，这限制了我们对学习率的加大。反过来说，如果能保持接近正确的方向，就意味着我们可以加大学习率。

基本的想法就是计算梯度的指数加权平均数，并利用该梯度更新你的权重。

具体执行：

首先V_dw 初始化为0，V_db 也初始化为0，V_dw 与dW、W同维度，V_db 与db、b同维度

在第t次迭代中，计算出dw和db，

V_dw = β V_dw + (1 - β)dW

V_db = β V_db + (1 - β)db

W - = α V_dw

b -= α V_db

其中β和α都是超参数，β的最佳值为0.9

RMSprop

它的全称是 root mean square prop 算法，它也可以加速梯度下降。

首先S_dw 初始化为0，S_dB 也初始化为0，S_dw 与dW、W同维度，S_dB 与dB、B同维度

在第t次迭代中，计算出dw和dB，

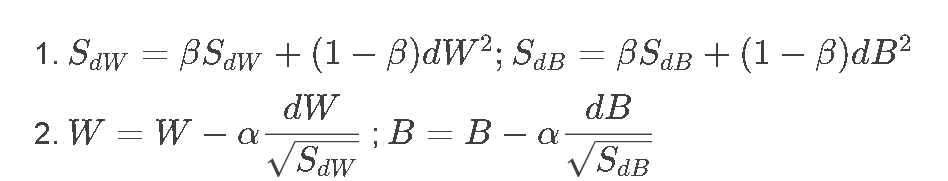
理解：

如果dB比较大，S_dB 也比较大，除一个比较大的数就变得很小，这样就消除了摆动，使得算法一直向最优方向推进。

如果S_dB的平方根趋近于 0 怎么办？

为了保证数值的稳定，我们要在分母的根号里加一个很小很小的ε(ε可以是10^-8)

Adam优化算法

Adam 优化算法基本上就是将 Momentum 和 RMSprop 结合在一起。

其中α、β₁、β₂ 、ε都是参数，β₁一般默认为0.9，₁、β₂一般默认为0.99，ε一般为10^-8 ，唯一需要不断调整的是α。

学习率衰减

如果α一直保持不变，可能永远不会收敛，而只是在附近摆动，为了收敛，我们需要在后期减小α。

在初期的时候，α可以适当的大一点，然后不断较小α。

假设我们使用mini-batch梯度下降，先将训练集分成若干min-batch，如下：

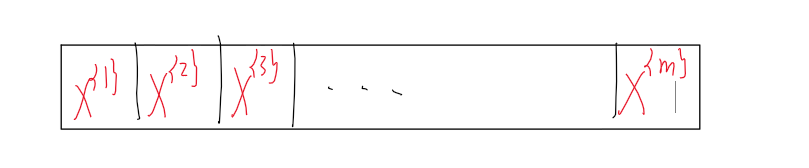
规定遍历一遍训练集(也就是遍历完所有的mini-batch)叫做一代，第一次遍历训练集叫做第一代。第二次就是第二代…

所以可以将α设置为这样：

α还有其他设置方法：

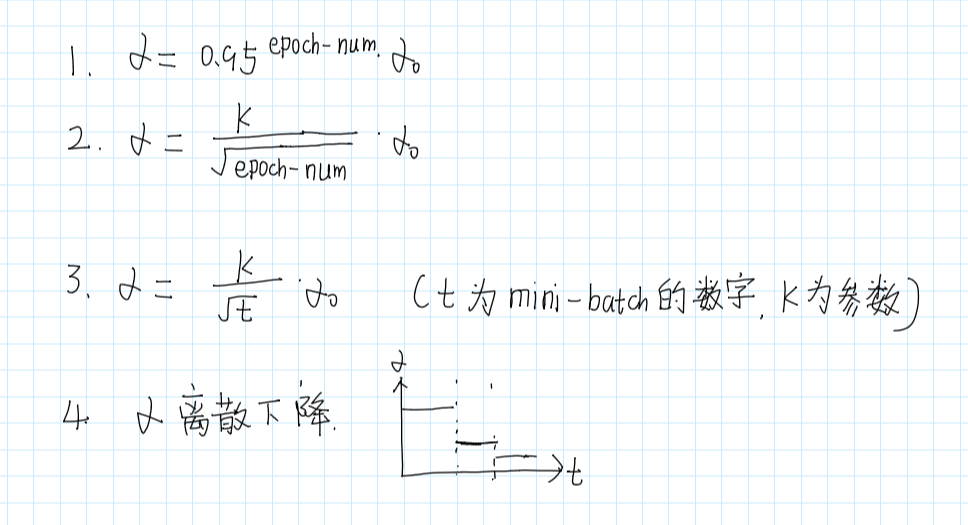
还有手动调节方法：就是你盯着你的模型，如果发现慢了，就自己调一下，有很多人在这么干，但是如果同时训练太多模型，这种方式就不实用了。

局部最优的问题

在深度学习研究早期，人们总是担心优化算法会困在极差的局部最优，不过随着深度学习理论不断发展，我们对局部最优的理解也发生了改变。

例如下面这张图：从图中可以看出J是关于w1、w2的函数，J有多个局部最优点，因此算法可能会困于局部最优中。

但是这仅仅是低维可能出现的情况。如果创建一个神经网络，梯度为0的点往往不是局部最优的点，而是鞍点(就像马鞍的形状)，如下图：

这是因为一个神经网络往往有许多的参数，因此J是定义在高维空间的函数。

虽然不会困在局部最优，但是当到达鞍点时，梯度为0或者趋于0，因此下降的会很慢，这就是为什么我们要优化的原因。

代码总结

python中的切片

在Python中a[i:j]表示复制字符串或数字从a[i]到a[j-1]（也称【切片】）。

1. numpy数组正切片

一维数组

• [start：end]

a = np.array([1, 2, 3, 4, 5])
print(a[1:3])  # 切片
>>>[2 3]

• 我们还可以定义步长，[start：end：step]。

a = np.array([1, 2, 3, 4, 5])
print(a[1:5:2])  # 切片(每隔两个取一次)
>>>[2 4]

注意：

• 如果我们不传递 start，则将其视为 0。
• 如果我们不传递 end，则视为该维度内数组的长度。
• 如果我们不传递 step，则视为 1。

二维数组

切片时特别要注意维度的变化

import numpy as np
a = np.array([
    [1, 2, 3, 4],
    [5, 6, 7, 8],
    [9, 10, 11, 12]
])
print(a[:, [1,2]])  # 输出第1列和第2列，输出的是3*4维数组
>>>[[ 2  3]
 [ 6  7]
 [10 11]]
 
print(a[:, 1])  # 第1列，输出的是一维数组
>>>[ 2  6 10]

import numpy as np
a = np.array([
    [1, 2, 3, 4],
    [5, 6, 7, 8],
    [9, 10, 11, 12]
])
print(a[0, 3])  # 第0行，第3列
>>>4
print(a[:, 3])  # 第3列 ，返回的是一维数组
>>>[4 8 12]
print(a[0, :])  # 第0行
>>>[1 2 3 4]

2. numpy数组负切片

• 使用减号运算符从末尾开始引用索引：[-start：-end]。

从倒数第start个到倒数第一个(不包括倒数第一个)

import numpy as np
arr = np.array([1, 2, 3, 4, 5, 6, 7])
# 从末尾开始的索引 3 到末尾开始的索引 1，对数组进行切片：
print(arr[-3:-1])
>>>[5 6]

3. 使用step的切片

一维：

import numpy as np
arr = np.array([1, 2, 3, 4, 5, 6, 7])
print(arr[1:5:3])  # 从索引 1 到索引 5，返回相隔的元素
>>>[2 5]
print(arr[::2])  # 返回数组中相隔2的元素
>>>[1 3 5 7]

二维：

import numpy as np
arr = np.array([[1, 2, 3, 4, 5], [6, 7, 8, 9, 10]])
print(arr[1, 1:4])  # 从第二行开始，对从索引 1 到索引 4（不包括）的元素进行切片
>>>[7 8 9]

4. numpy中索引数组切片

import numpy as np
x = np.array([[1, 2], [3, 4], [5, 5]])
y = x[[0, 1, 2], [0, 1, 0]] # 提取(0,0),(1,1),(2,0)位置的元素
print(y)
>>>[1 4 5]

import numpy as np
x = np.array([[0, 1, 2], [3, 4, 5], [6, 7, 8], [9, 10, 11]])
# 切片模式一：输出结果写入单列表
rows = np.array([0, 3, 0, 3])
cols = np.array([0, 0, 2, 2])
y = x[rows, cols] # 取(0,0),(3,0),(0,2),(3,2)位置元素，y是一维数组
print(y)
>>>[ 0  9  2 11]

# 切片模式二：输出结果写入二维数组
rows = np.array([[0, 0], [3, 3]])
cols = np.array([[0, 2], [0, 2]])
y = x[rows, cols] # 取(0,0),(0,2),(3,0),(3,2)位置元素，y是2*2维数组
print(y)
>>>[[ 0  2]
 [ 9 11]]
 
# 切片模式二：输出结果写入2*3的数组
rows = np.array([[0, 0, 1], [3, 2, 3]])
cols = np.array([[0, 2, 1], [0, 1, 2]])
y = x[rows, cols] # 取(0,0),(0,2),(1,1),(3,0),(2,1),(3,2)位置元素，y是2*3维数组
print(y)
>>>[[ 0  2  4]
 [ 9  7 11]]

5. 切片与索引数组的组合

import numpy as np
a = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])
print(a)
>>>[[1 2 3]
 [4 5 6]
 [7 8 9]]
 
b = a[1:3, 1:3] # 取第一行到第三行(不包括第三行)与第一列到第三列(不包括第三列)相交的元素，y是2*2维数组
print(b)
>>>[[5 6]
 [8 9]]
 
c = a[1:3, [1, 2]] # 取第一行到第三行(不包括第三行)与第一列和第二列相交的元素，y是2*2维数组
print(c)
>>>[[5 6]
 [8 9]]
 
d = a[..., 1]  # arr[..., 1] 等价于 arr[: , 1] # 输出第1列的元素，y是一维数组
print(d)
>>>[2 5 8]

---

np.random.permutation()

np.random.permutation()：随机排列序列。

1. 对0-m(不包括m)之间的序列进行随机排序

import numpy as np
b = np.random.permutation(5)  # 这里m=5
print(b)
>>>[3 2 1 0 4]

2. 对一个list进行排序

import numpy as np
a = np.random.permutation([1, 2, 3, 4, 5, 6])
print(a)
>>>[3 4 2 5 1 6]

如果list是多维的，只在列进行随机排列

import numpy as np
a = np.arange(9).reshape(3, 3)
print(a)
>>>[[0 1 2]
 [3 4 5]
 [6 7 8]]
 
b = np.random.permutation(a)
print(b)
>>>[[3 4 5]
 [0 1 2]
 [6 7 8]]

---

np.zeros_like()

np.zeros_like(a) # 构建一个和a同维的零矩阵

---

math.floor()

返回小于参数x的最大整数,即对浮点数向下取整

---

matplotlib.pyplot

matplotlib最流行的Python底层绘图库。

画图第一步都是先创建一个画板figure

import matplotlib.pyplot as plt
fig = plt.figure()

figure就好像是画板，是画纸的载体，但是具体画画等操作是在画纸上完成的。在pyplot中，画纸的概念对应的就是Axes/Subplot。

在英文中，axis是轴的意思，axes是axis的复数形式，可以看成是轴域(一个坐标轴就是一个轴域)

例1：用subplot()画图

import matplotlib.pyplot as plt
fig = plt.figure()
ax = fig.add_subplot(211) #添加子图  括号中前两个参数表示生成2行1列的子图矩阵，第三个参数就是图的编号
# xlim[x轴刻度最小值，x轴刻度最大值]
ax.set(xlim=[0.5, 4.5], ylim=[-2, 8], title='An Example Axes', ylabel='Y-Axis', xlabel='X-Axis')
plt.show()

例2：用add_axes()画图

import matplotlib.pyplot as plt
fig = plt.figure()
ax3 = fig.add_axes([0.1, 0.1, 0.8, 0.8])  # [left,bottom,width,height]
ax4 = fig.add_axes([0.72, 0.72, 0.16, 0.16])
plt.show()

总结：

其实两种方法都可以画图，但用add_axes()更加的灵活，可以随意调整子图的位置。

---

plt.gca() 获取当前子图(Axes对象)