Weight Initialization in Deep Neural Networks

From: https://towardsdatascience.com/weight-initialization-in-deep-neural-networks-268a306540c0

了解神经网络中不同的权重初始化方法

权重和偏置是神经网络的可调参数，在训练阶段，使用梯度下降算法改变它们，以最小化网络的成本函数。然而，在开始训练网络之前，必须对它们进行初始化，这个初始化步骤对网络训练有重要影响。在这篇文章中，我将首先解释weight初始化的重要性，然后讨论可用于此目的的不同方法。

Feedforward neural networks

在讨论权重初始化方法之前，我们简单回顾一下支配前馈神经网络的方程。关于这些方程的详细讨论，你可以参考参考文献[1]。假设你有一个如图1所示的前馈神经网络。

这个表示网络的输入向量。每个 x_i 是一个输入特征。网络有L层，第l层的神经元数量为 n^[l] 。输入层被认为是零层。所以输入特征的数量为n^[0]。第l层中的神经元i的输出或激活是 a_i^[l]。

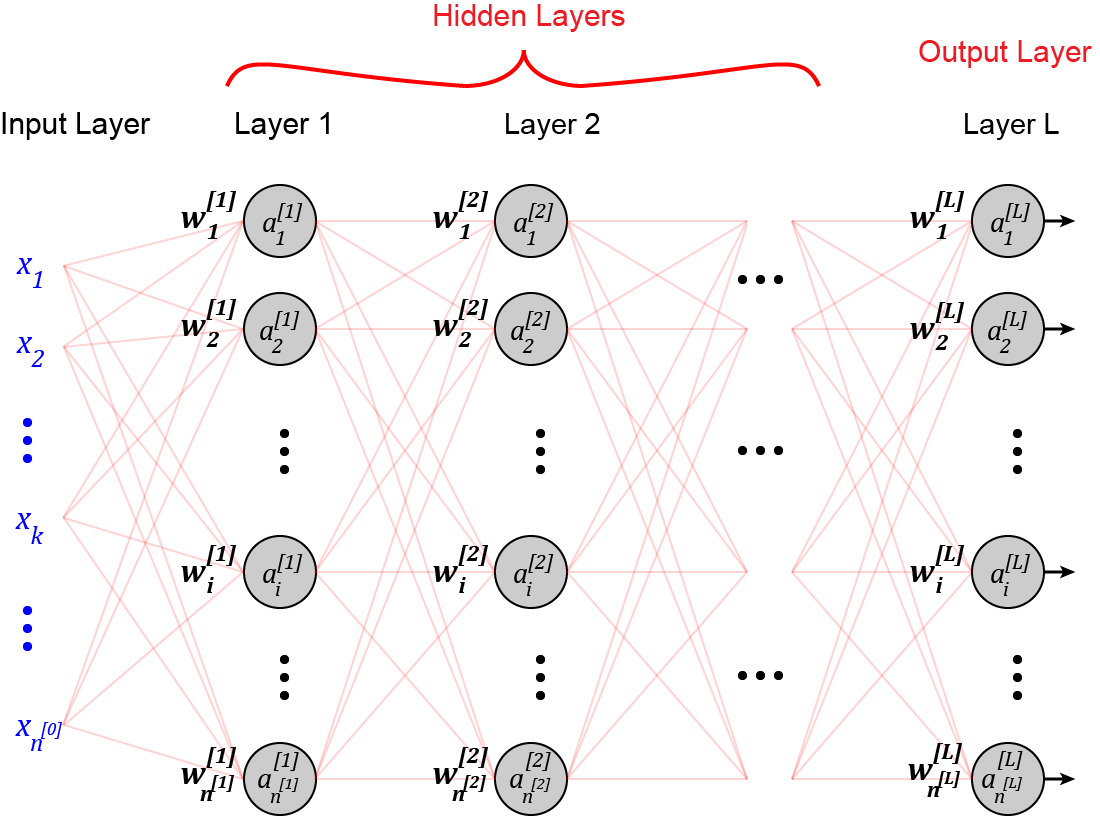
第l层中的神经元i的权重可以用向量表示

其中w_ij^[l]代表输入j（来自l-1层的神经元j）进入l层的神经元i的权重（图2）。

在第l层，每个神经元接收前一层所有神经元的输出，再乘以其权重，w_i1, w_i2, … , w_in。加权的输入被加在一起，一个叫做偏置的常数（b_i^[l]）被加到它们上面，产生神经元的净输入

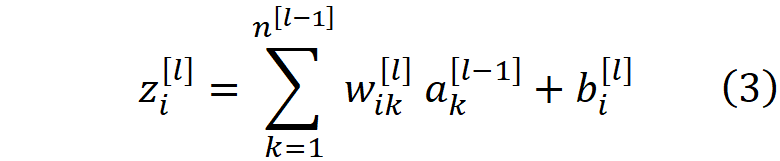
第l层神经元的净输入可以用向量表示

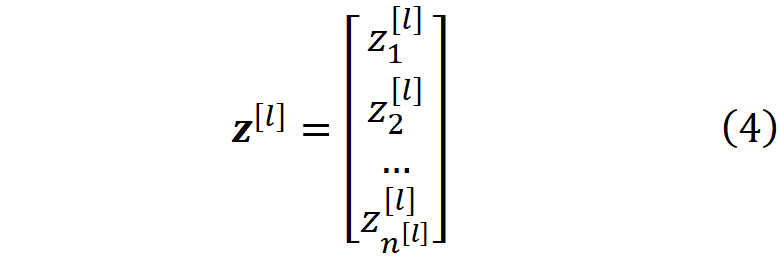
同样地，第l层神经元的激活可以用激活向量表示

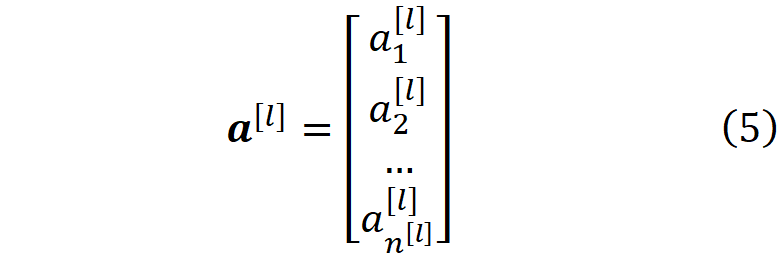
其中求和已被权重和激活向量的内积所取代。然后，网络输入通过激活函数g，产生神经元i的输出或激活。

我们通常假设输入层为零层，而

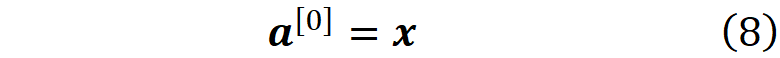
因此，对于第一层，公式7被写为

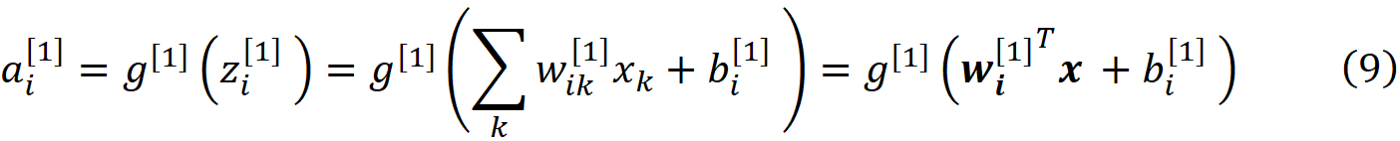
我们可以将一个层的所有权重合并为该层的权重矩阵

所以W^[l]是一个n^[l]×n^[l-1]矩阵，这个矩阵的（i,j）元素给出了从l-1层的神经元j到l层的神经元i的连接权重。 我们也可以为每一层设置一个偏置向量

现在我们可以把公式6写成一个矢量的形式

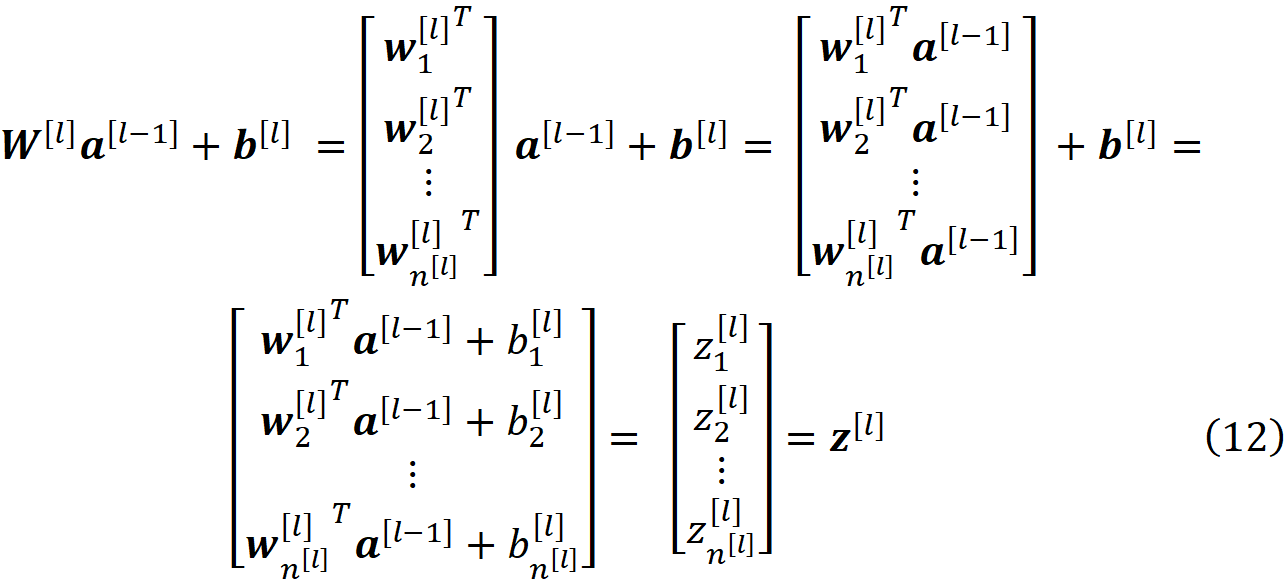
而利用公式7，我们得到

我们通常用yhat来表示输出层的激活。

https://miro.medium.com/max/1400/1*FRb2rkJnn8nlVavsWdc4Pg@2x.png

而向量y表示输入向量的实际标签（公式1）。对于二元分类，y只有一个元素，可以认为是一个标量。但是对于多类和多标签分类，它是一个单热或多热的编码向量（更多细节请参考[1]）。在反向传播过程中，我们首先计算最后一层的神经元i的误差。误差被定义为损失函数相对于净输入的部分导数

误差是衡量这个神经元在改变整个网络的损失函数方面的效果。 然后我们用这个误差项来计算前一层的神经元的误差

这样，我们用上一层的误差项来计算每一层的误差项，直到我们到达第一层。我们可以用每层的误差项来计算损失函数关于权重和偏置的梯度

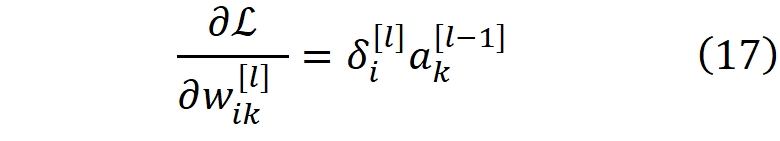
利用它们，我们可以为梯度下降的下一步更新权重和梯度的值。

The importance of random weight initialization

我们可以用于权重初始化的最简单方法是为所有权重分配一个常数。例如，我们可以将所有权重初始化为零。然而，事实证明这是一个坏主意。让我更详细地解释一下。假设我们有一个神经网络（称为网络 A），有 L 层，每层有 n^[l] 个神经元。现在对于网络的每一层，我们用常数值 ω^[l] 初始化权重矩阵，用常数值 β^[l] 初始化偏置向量。所以在第 l 层我们有

请注意，两个不同的层可以有不同的ω^[l]和β[l]的值。如果我们用公式21初始化权重和偏置，那么可以证明，在梯度下降的每一步中，每一层的权重和偏置都是相同的（证明见附录）。所以我们可以假设在一个数据集上训练网络A后，其权重和偏置会收敛到ω_f^[l]和β_f[l]。所以在每一层中，所有神经元的权重和偏置都是一样的。

现在假设我们有第二个网络（称为网络B），它的层数相同，而且每层只有一个神经元。为了能够比较网络A和B，我们用上标 <B> 来表示属于网络B的数量，两个网络如图3所示。

在每一层，两个网络都有相同的激活函数，而且它们也有相同的输入特征，所以

我们用β^[l]初始化所有的偏置值（来自公式21）。对于第一层，我们用相同的网络A值初始化权重矩阵（公式10）。

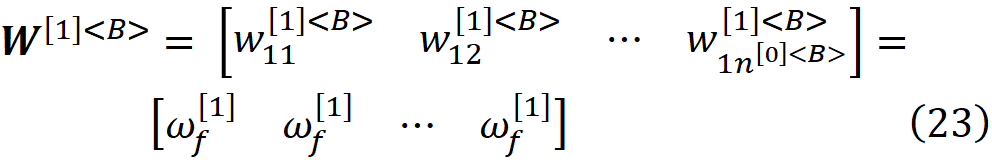
由于我们只有一个神经元和n^[0]<B>输入特征，所以权重矩阵确实是一个行向量。这个矩阵的每个元素都是常量值ω_f^[1]。对于接下来的层，我们将权重矩阵定义为

其中n^[l]是网络A中第l层的神经元数量。由于我们在第l≥1层只有一个输入的神经元，所以权重矩阵只有一个元素，这个元素是ω_f^[l] n^[l]。因此，对于网络B的每一层l≥1，我们用网络A的权重乘以网络A同一层的神经元数量来初始化权重矩阵。现在我们可以很容易地证明（证明在附录中给出），网络B与网络A是等价的，这意味着对于相同的输入向量，它们在梯度下降和收敛后产生相同的输出。

因此，通过使用这种对称的权重初始化，网络A的行为就像网络B一样，它的学习能力是有限的，然而，计算成本仍然是相同的。用相同的值初始化网络的所有权重和偏置是这种方法的一个特例，它导致了同样的问题。最糟糕的情况是，我们把所有的权重都初始化为零。在这种情况下，根据公式16，除了最后一层外，所有层的误差项都是零，所以损失函数的梯度也将是零（公式19和20）。因此，这些层的权重和偏置将不会被更新，网络根本无法被训练。

一个神经网络可以被认为是一个有两个元素的矩阵。它的深度是指层数，宽度是指每层的神经元数量（为简单起见，假设所有层的神经元数量相同）。在所有层中使用线性激活函数可以缩小网络的深度，因此它的表现就像一个只有一层的网络（证明见[1]）。使用对称权重和偏置初始化会缩小网络的宽度，所以它表现得像一个每层只有一个神经元的网络（图4）。

因此，为了打破对称性，权重或偏差都不应该以这种方式初始化。在实践中，我们对权重使用随机初始化，对所有的偏差使用零或一个小数字初始化。选择权重是为了这个目的，因为它们适当的随机初始化不仅打破了对称性，而且还有助于解决下一节讨论的梯度消失和爆炸问题。

Vanishing and exploding gradients

使用反向传播方程（公式15和16），我们可以计算出网络中任何一层的误差项。假设我们想计算第l层的误差项。我们首先计算输出层的误差项，然后向后移动，计算前面各层的误差项，直到我们到达第l层。

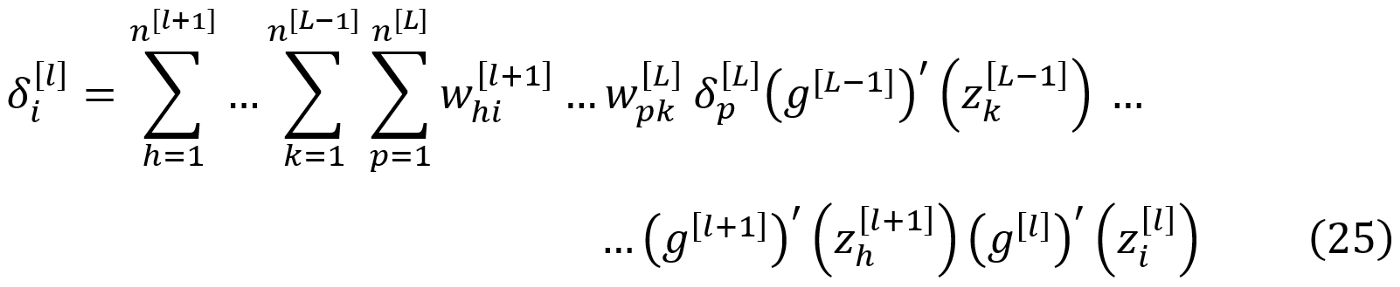
你可以参考[1]了解这个方程的推导。基于这个方程，误差向量的每个元素（也就是该层的一个神经元的误差）都与下一层的神经元的权重的连锁乘法成正比。现在，如果权重是小数字，这些权重的链式乘法可能会导致极小的误差项，特别是如果你有一个有这么多层的深度网络。因此，误差向量的一些或全部元素将非常小。

根据公式17和18，损失函数和成本函数的梯度与误差项成正比，所以它们也将成为一个非常小的数字，这导致梯度下降中权重和偏置更新的步长非常小（公式19和20）。最后的结果是梯度下降法和网络的学习过程变慢。这就是所谓的梯度消失问题。

也有可能，权重是非常大的数字。那么，这些的链式乘法就会变成一个非常大的数字，梯度下降中的梯度和步长就会爆炸。其结果是一个不稳定的网络，梯度下降步骤不能收敛到权重和偏差的最佳值，因为现在的步骤太大，错过了最佳点。这被称为爆炸性梯度问题。我们可以使用权重初始化技术来解决这些问题。

Mean and variance rules

在讨论初始化方法之前，我们需要回顾一下均值和方差的一些特性。我们用E[X]表示随机变量X的平均值，用Var(X)表示其方差。如果X_1, X_2, … … ，X_n是具有有限平均数的独立随机变量，如果a_1, a_2, … … ，a_n和b是任意的常数，那么

此外，如果X和Y是两个独立的随机变量，那么我们有

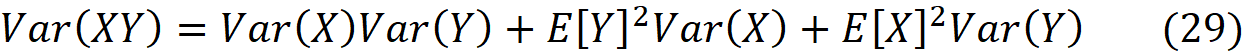
方差也可以用均值来表示。如果我们有一个随机变量X，那么

Random initialization methods

接下来的章节将介绍的初始化方法是基于随机权重初始化来打破对称性。然而，由于权重不再是对称的，我们可以安全地将所有偏置值初始化为相同的值。所以在所有这些方法中，偏置值都被初始化为零。这些初始化方法是基于一些假设，将在下一节讨论。

Assumptions

Assumptions 1- 我们假设每层的权重是独立和相同的分布（IID）。它们被初始化为均值为0、方差为Var(w^[l])的均匀或正态分布。

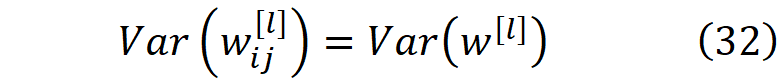
每一层的权重都与其他层的权重无关。

Assumptions 2-特征输入也被假定为独立和相同分布（IID）。特征输入是独立于权重的。此外，它们被归一化，所以

我们还需要对激活函数做一个假设。我们有两种类型的激活函数。一种是在z=0时可分的（如sigmoid），另一种是不可分的（如ReLU）。如果激活函数在z=0时是可分的，那么当z很小的时候，我们可以用Maclaurin系列来近似它。一个函数的Maclaurin级数定义为

可以用来计算x接近零时f(x)的近似值。tanh的Maclaurin数列是

sigmoid 的麦克劳林级数是

对于较小的 z 值，我们可以写

因此，当z接近于零时，sigmoid和tanh可以用线性函数来近似，我们说我们处于这些函数的线性系统中。由于我们假设输入特征是归一化的，它们的值在第一次迭代时相对较小，如果我们用小数字初始化权重，那么神经元的净输入（z_i^[l]）最初会很小。所以我们假设。

Assumptions 3-激活函数在第一次迭代时处于线性状态。

现在基于这些假设，我们可以得出一些结论：

Conclusion

1-在梯度下降的第一次迭代中，每一层的神经元的权重，以及上一层的神经元的激活是相互独立的。此外，在每一层中，所有的激活都是独立的。

根据公式3、7和9，我们有

其中的偏置被假定为零。所以a_k^[l-1]可以从上一层的激活量递归计算，直到我们到达第一层，a_i^[l]是输入特征和第1至l层权重的非线性函数

由于每一层的权重都是独立的，并且它们也独立于x_j和其他层的权重，它们也将独立于权重和x_j的函数（公式42中的f）。所以w_kp^[l]和a_i^[l-1]对于i、p、k和l的所有值都是独立的。

此外，由于所有的权重都是独立的，输入特征也是独立的，它们的函数（f（w_kp^[m], x_j））也是独立的。所以在第l-1层，所有的a_i^[l-1]都是独立的，这意味着在每一层，所有的激活都是独立的。当然，如果我们在输出层有softmax激活函数的话，这就不是真的了。Softmax被定义为

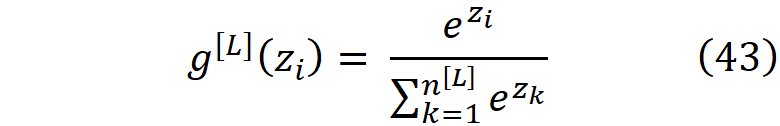
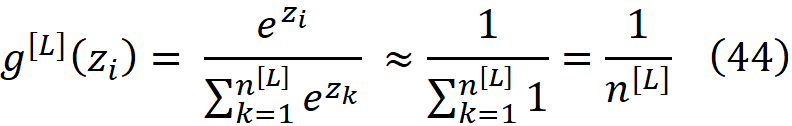
因此，softmax函数的输出对所有神经元来说大致相同，只是输出层中神经元数量的函数。因此，我们可以假设激活仍然不依赖于彼此或该层的权重。

2- 在第一次迭代期间，每层净输入的平均值为零。

利用公式6、26和28以及权重和激活在第一次迭代中是相互独立的这一事实，我们可以写出

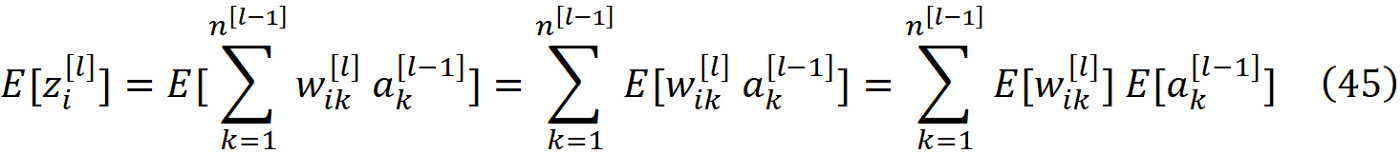
基于第一个假设，权重的平均值为零（公式31）。因此，对于所有的l的值，我们有

类似地，我们可以使用方程。 6、27 和 29 得到

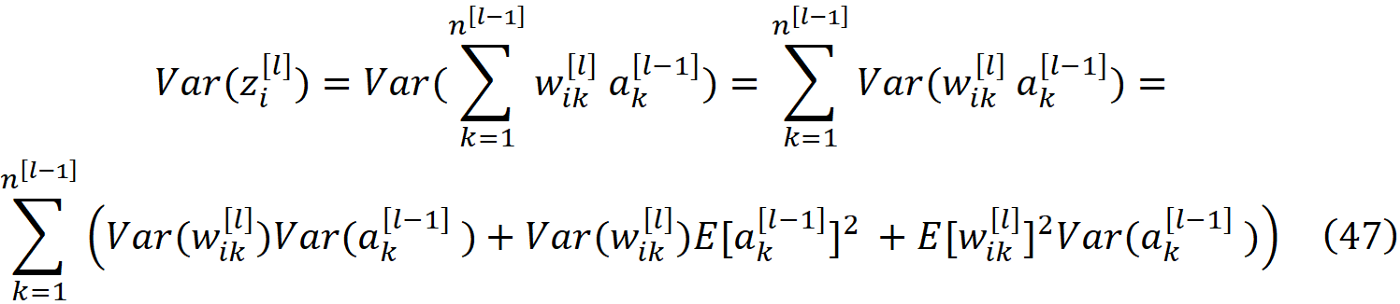
使用公式31和32，前面的方程可以被简化:

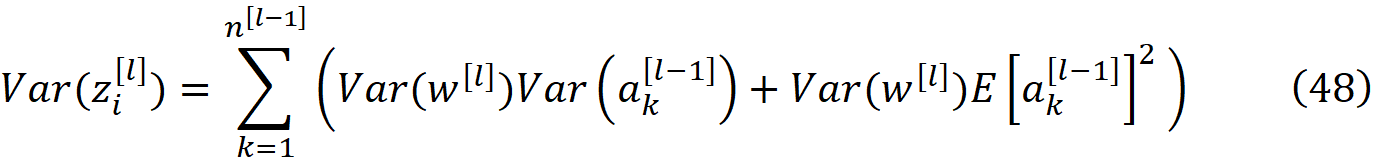
LeCun weight initialization

这种方法是由LeCun等人首次提出的[2]。如前所述，我们要防止在反向传播过程中梯度的消失或爆炸。所以我们不应该让公式25中的误差消失或爆炸。每一层的误差是输出层误差（δ^[L]）的一个函数。另一方面，输出层的误差，是输出层激活的函数（公式15）。因此，如果在前向传播过程中，激活值消失或爆炸，错误也会发生同样的情况。因此，我们应该在前向传播过程中防止各层激活的爆炸或消失。

方差代表了数据在其平均值周围的分布，所以如果第l层的激活的平均值和方差与第l-1层的大致相等，那么这意味着激活不会从第l-1层到第l层消失或爆炸。

对于l=1，前一层的激活是输入特征（公式8），其方差等于1（公式34）。所以前面的方程式可以写成

这种LeCun方法只适用于在z=0处可微的激活函数。它最初是针对tanh激活函数推导的，但也可以扩展到sigmoid。

Tanh activation functions

对于tanh，我们可以使用公式37和48来写出

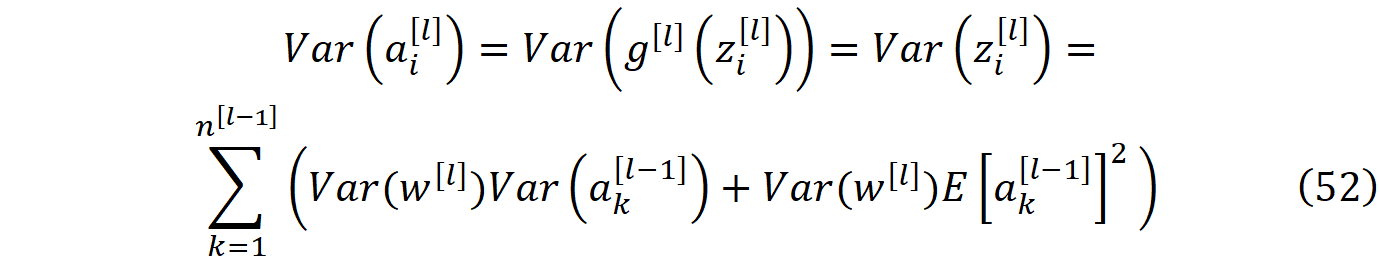
使用方程37、46 和 49 我们得到：

因此，公式49中的条件得到了满足，激活的平均值在不同层中没有变化。将公式53代入公式52，并利用一个层中所有激活的方差是相同的事实（公式51），我们得到

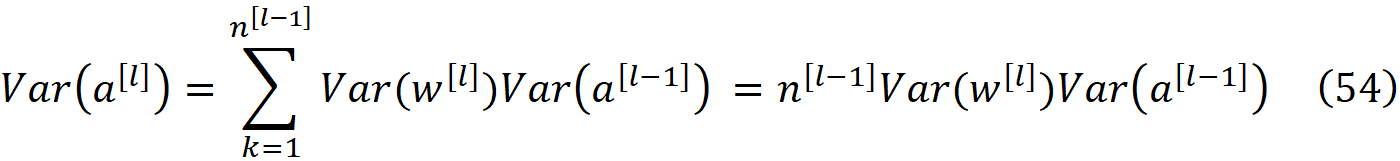
现在为了满足公式51的条件，我们应该有:

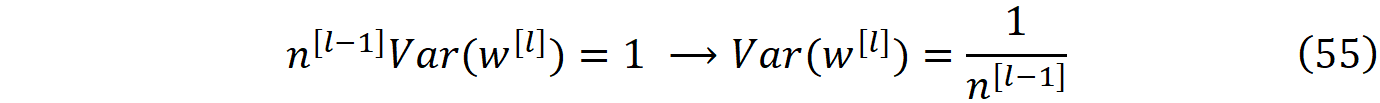
这就是LeCun初始化公式。如果我们假设权重具有正态分布，那么我们需要从均值为0、方差为1/n^[l-1]的正态分布中挑选权重。我们也可以对权重使用均匀分布。如果我们在区间[a, b]上有一个均匀分布，其平均值将是(a+b)/2，并且方差是(b-a)^2/12

因此，如果我们从区间内的均匀分布中挑选每层的权重:

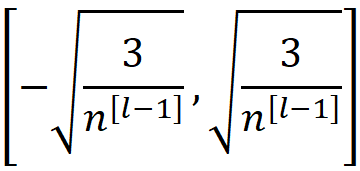
它的平均数将为零，其方差将与公式55中给出的方差相同。

Xavier weight initialization

Lecun方法只考虑到了输入信号的前向传播。我们也可以把前面的讨论扩展到反向传播。在此基础上，Xavier Glorot等人[3]提出了另一种包括信号的反向传播的方法。

Backpropagation

输出层中每个神经元的误差在公式15中给出。所以δ^[L]是输出层的激活（yhat）和标签向量（y）的函数。我们已经表明，在每个层中，所有的激活都是独立的。对于二元分类，y只有一个元素（在这种情况下是标量y）。对于多类和多标签分类，它是一个单热或多热的编码向量，显然，所有元素都是相互独立的。所以输出层的神经元的误差是一些独立变量的函数，它们将是相互独立的。对于公式37中的tanh，我们得到

将此方程代入公式16，我们可以得到

所以δ_i^[l]可以从下一层的误差递归计算，直到我们到达输出层，它是输出层的误差和l+1到L层的权重的线性函数。

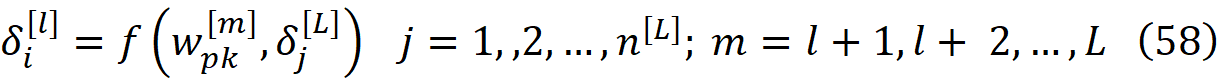
我们已经知道，第l层的所有权重（w_ik^[l]）是独立的。输出层的误差是独立的。权重和误差并不完全独立。因为误差取决于输出层的激活，可以写成网络的权重的函数（公式42）。然而，每个权重w_pk^[l]只用于产生第l层的神经元p的激活。由于我们有这么多层，通常每层有这么多神经元，单个权重对输出层的激活和误差的影响可以忽略不计，所以我们可以假设输出层的每个激活与网络中的每个权重无关。
因此，我们也可以假设每层的误差与该层的权重无关。现在使用这个假设和公式26、28和57，我们可以得到

现在我们可以使用这个方程和方程27、29、31 和 32:

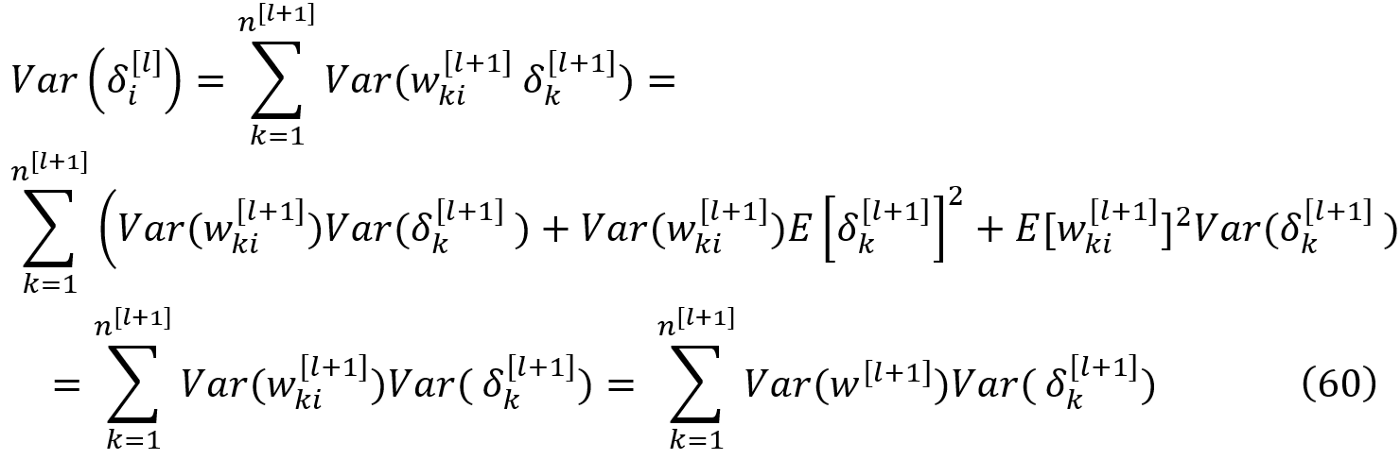
基于这个方程，δ_i^[l]不是i的函数，这意味着每一层的所有误差的方差是相同的。

所以我们可以简化公式60，写成

与正向传播类似，所有层的误差平均值都是一样的（公式59），我们希望方差保持不变。因此，从公式62，我们得到

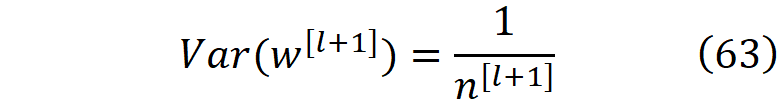
正如你所看到的，在反向传播中，每一层的权重方差等于该层神经元数量的倒数，然而，在正向传播中，等于前一层神经元数量的倒数。为了解决这一冲突，我们可以从正态分布中挑选每一层的权重，其均值为零，方差为

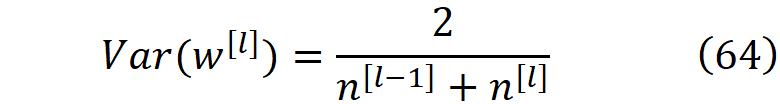
这个方差是公式55和63中给出的方差的谐波平均值。这就是Xavier的初始化公式。我们也可以对权重使用均匀分布。因此，如果我们从区间内的均匀分布中挑选每层的权重

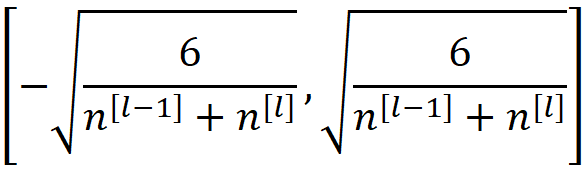
它的平均数将为零，其方差将与公式64中给出的方差相同。

Kumar initialization for sigmoid activation functions

Kumar[4]研究了神经网络中的权重初始化问题。他提出了一个适用于任何任意可微分激活函数的通用权重初始化策略，并利用它推导出了sigmoid激活函数的初始化参数。这里我们不打算讨论他的方法。相反，我们扩展Xavier的方法，将其用于sigmoid激活函数。我们可以使用公式27、39和48来写出

使用公式26、39和46，我们得到

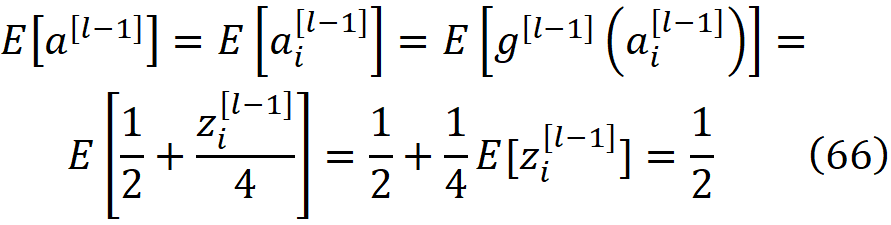
将公式66代入公式65，并利用一个层中所有激活的方差是相同的事实（公式50），我们得到

但我们知道，每层激活的方差是1（公式51），所以我们可以简化前面的公式:

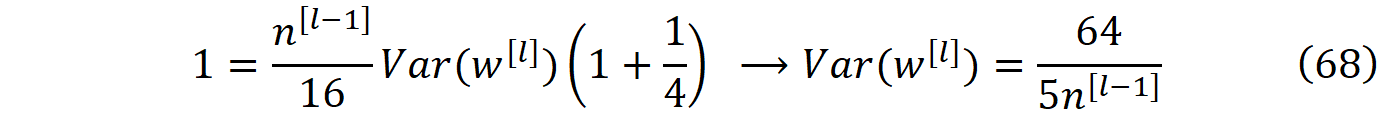
这是Kumar得到的结果，他认为没有必要在反向传播过程中为激活的方差再设置一个约束条件。所以你可以从正态或均匀分布中挑选权重，其方差在公式68中给出。然而，我们也可以研究反向传播。对于反向传播，我们首先需要计算误差的平均值。根据公式39，我们有

因此误差的均值是：

他们的方差将是

因此，为了保持不同层的方差相同，我们应该有

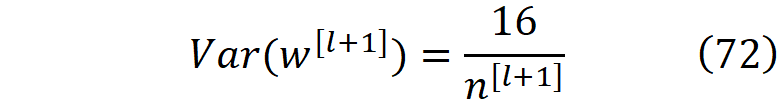
如果我们假设权重具有正态分布，它的平均值为零，其方差可以从公式68和72的调和平均值中获取。

He weight initialization

这种方法是由He等人[5]首次提出的。如果我们有一个激活函数在z=0处不可微分（如ReLU），那么我们就不能用Maclaurin系列来近似它。因此，Xavier方法不能再使用了，我们应该使用另一种方法。

ReLU activation function

它在z=0时是不可微的，我们通常假设它的导数在这一点上是0或1，以便能够进行反向传播。然而，当z接近于零时，我们不能用Maclaurin数列来近似它。从公式49我们可以得出

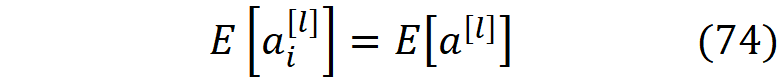
为了使用He初始化方法，我们从公式48开始，并使用公式30、51和74来简化它

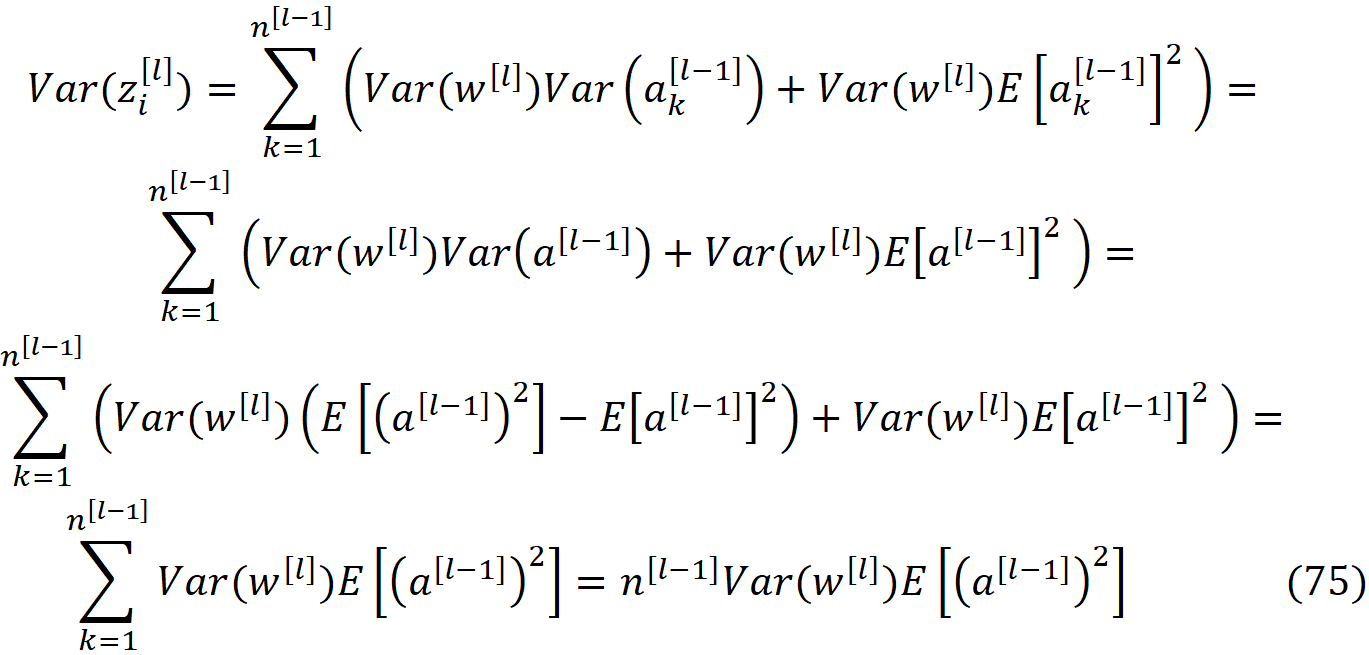
根据公式75，z_i^[l]的方差对第l层的所有神经元都是一样的。 所以我们可以写成

回顾一下，我们假设权重具有均匀或正态分布，平均值为零。所以它们应该有一个围绕零的对称分布。我们知道

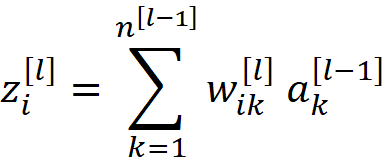
所以z_i^[l]可以被看作是权重的线性组合。我们还知道，它的平均值是零（公式46），所以它也应该有一个围绕零的对称分布。因此，它的分布是一个偶函数。现在我们可以写出

因为积分项是一个偶函数。根据ReLU激活的定义（公式73），我们有

因此，使用公式77和78，我们有

现在我们可以使用公式30，写出

因此，使用公式74和76，我们得到

通过将公式81替换成公式75，我们可以得到

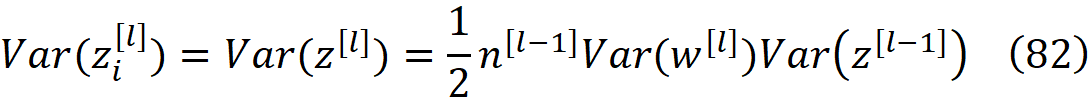
为了防止在前向传播过程中各层激活的爆炸或消失，我们应该确保净输入不会爆炸或消失，所以第l层的净输入的方差应该大致等于第l-1层的方差。因此，从前面的等式中，我们得出的结论是

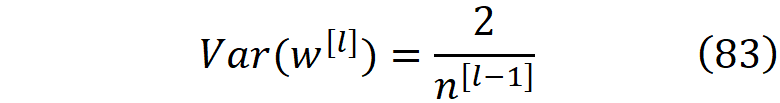
Backpropagation

如前所述，虽然ReLU在z=0处不可微，但我们假设它的导数在这一点上是零或一（这里我们假设它是一）。所以ReLU的导数是

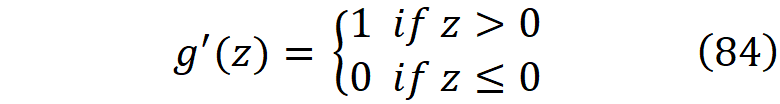
由于g’(z)的一半数值是1，另一半是0，其平均值将是

而g’(z)的每个值离其平均值的距离将是0.5。所以我们可以写成

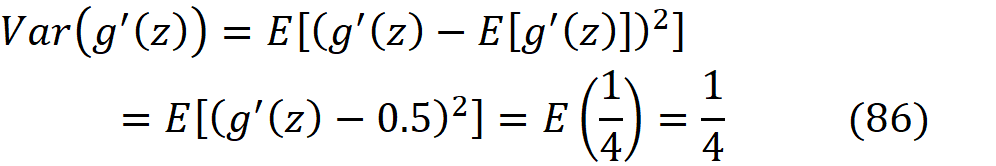
g’(z_i^l)是z_il的函数，而δ_k^[l+1]对z_i[l]的依赖性非常弱，所以我们可以假设g’(z_i^l)和δ_k[l+1]是独立的。此外，g’(z_i^l)独立于第l+1层的权重。因此，我们可以写成

根据公式16和29，我们可以写出

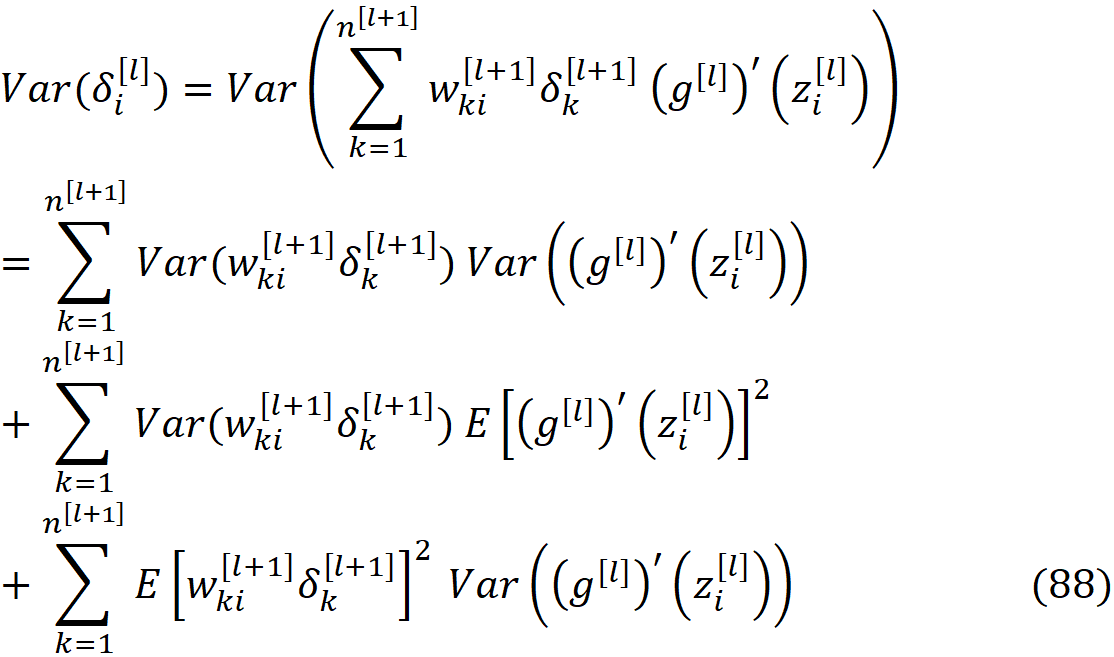
正如我们为Xavier方法所展示的那样，单个权重对输出层的激活和误差的影响可以忽略不计，所以我们可以假设输出层的每个激活与网络中的每个权重无关。所以

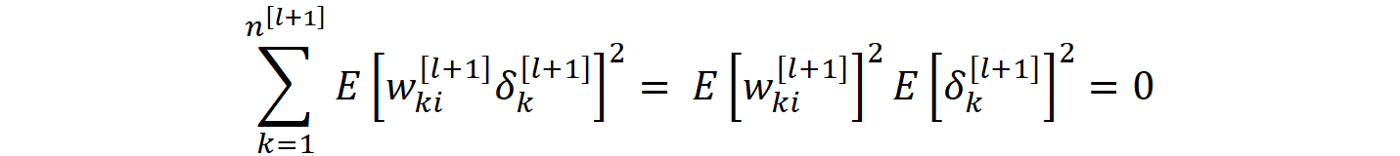
而公式88右边的最后一项成为零。将g’(z)的平均值和方差插入公式88中，我们得到

现在我们可以用公式29、31、32和87来简化它

这个方程的右手边不取决于i，所以第l层的所有误差的方差是相同的，这对所有其他层也是如此。因此，我们可以写成

与Xavier方法类似，所有层的误差平均值都是一样的，我们希望其方差保持不变。因此，从公式91中，我们得到

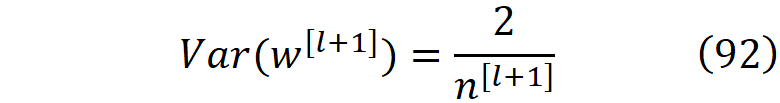
这个方差可以表示为公式83和92中给出的方差的调和平均值

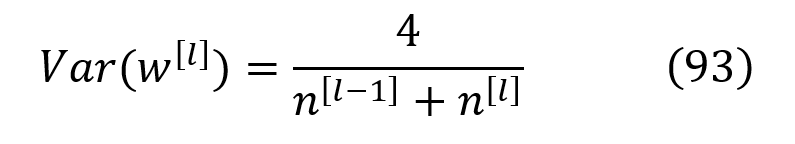
所以我们可以从均值为零、方差为公式93的正态分布中挑选权重。

本文讨论的权重初始化方法对训练神经网络非常有用。权重初始化方法可以打破对称性，解决梯度消失和爆炸的问题。对称的权重初始化可以缩减网络的宽度，限制其学习能力。将权重初始化为零，不允许更新权重和偏置。

权重初始化技术是基于随机初始化的。权重是从正常或均匀分布中挑选出来的。这个分布的平均数为零，其方差被仔细选择，以防止在梯度下降的第一次迭代中出现权重消失或爆炸。当激活函数是可微分的时候，LeCun和Xavier方法是有用的。然而，今天大多数的深度神经网络使用的是像ReLU这样的不可微分的激活函数。对于这样的激活函数，我们应该使用He初始化方法。

权重初始化是训练深度神经网络的一个重要部分。然而，需要注意的是，它们不能完全消除消失或爆炸性梯度问题。权重初始化方法只能在梯度下降的第一次迭代中控制权重的方差。在接下来的迭代中，权重会发生变化，以后仍然可能变得过小或过大。然而，适当的权重初始化可以延缓这一问题的发生，并使之在以后发生。通过在第一次迭代中控制权重的方差，网络可以在权重消失或爆炸之前有更多的迭代，所以它有更高的收敛机会。

Reference：

1. Bagheri, R., An Introduction to Deep Feedforward Neural Networks, https://towardsdatascience.com/an-introduction-to-deep-feedforward-neural-networks-1af281e306cd
2. LeCun Y.A., Bottou L., Orr G.B., Müller KR. Efficient BackProp. In: Montavon G., Orr G.B., Müller KR. (eds) Neural Networks: Tricks of the Trade. Lecture Notes in Computer Science, vol 7700. Springer (2012).
3. Glorot, X., Bengio, Y.: Understanding the difficulty of training deep feedforward neural networks. In: Proceedings of the Thirteenth International Conference on Artificial Intelligence and Statistics, pp. 249–256 (2010).
4. Kumar, S.K.: On weight initialization in deep neural networks. Preprint at arXiv:1704.08863 (2017).
5. Kaiming He, Xiangyu Zhang, Shaoqing Ren, and Jian Sun. Delving deep into rectifiers: Surpassing human-level performance on imagenet classification. In Proceedings of the IEEE international conference on computer vision, pp. 1026–1034 (2015).

---

参考：

1. https://fengzhe.blog.csdn.net/article/details/102856968?spm=1001.2101.3001.6650.1&utm_medium=distribute.pc_relevant.none-task-blog-2%7Edefault%7ECTRLIST%7Edefault-1.no_search_link&depth_1-utm_source=distribute.pc_relevant.none-task-blog-2%7Edefault%7ECTRLIST%7Edefault-1.no_search_link
2. https://www.deeplearning.ai/ai-notes/initialization/
3. https://xiaobaihaha0001.gitbook.io/tech-share/machinelearning/shen-du-xue-xi-chu-shi-hua-fang-fa
4. https://mp.weixin.qq.com/s/GLszj8EsoVHU1qWOc8bpaw