蝴蝶曲线(也称为蝴蝶效应曲线或洛伦兹吸引子)通常与混沌理论相关,特别是爱德华·洛伦兹的工作。洛伦兹吸引子是一个三维结构,它描述了某些动态系统的长期行为,即使这些系统的初始条件只有微小的变化也会导致截然不同的结果。
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
# 洛伦兹吸引子的参数
sigma = 10.0
beta = 8.0 / 3.0
rho = 28.0
# 时间步长
dt = 0.01
# 总时间
steps = 10000
# 初始化数组
xs = np.zeros((steps + 1,))
ys = np.zeros((steps + 1,))
zs = np.zeros((steps + 1,))
# 设置初始条件
xs[0], ys[0], zs[0] = (0., 1., 1.05)
# 使用洛伦兹方程进行积分
for i in range(steps):
dx, dy, dz = (
sigma * (ys[i] - xs[i]),
xs[i] * (rho - zs[i]) - ys[i],
xs[i] * ys[i] - beta * zs[i]
)
xs[i + 1] = xs[i] + dx * dt
ys[i + 1] = ys[i] + dy * dt
zs[i + 1] = zs[i] + dz * dt
# 绘制图形
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.plot(xs, ys, zs, lw=0.5)
ax.set_xlabel("X Axis")
ax.set_ylabel("Y Axis")
ax.set_zlabel("Z Axis")
ax.set_title("Lorenz Attractor")
plt.show()
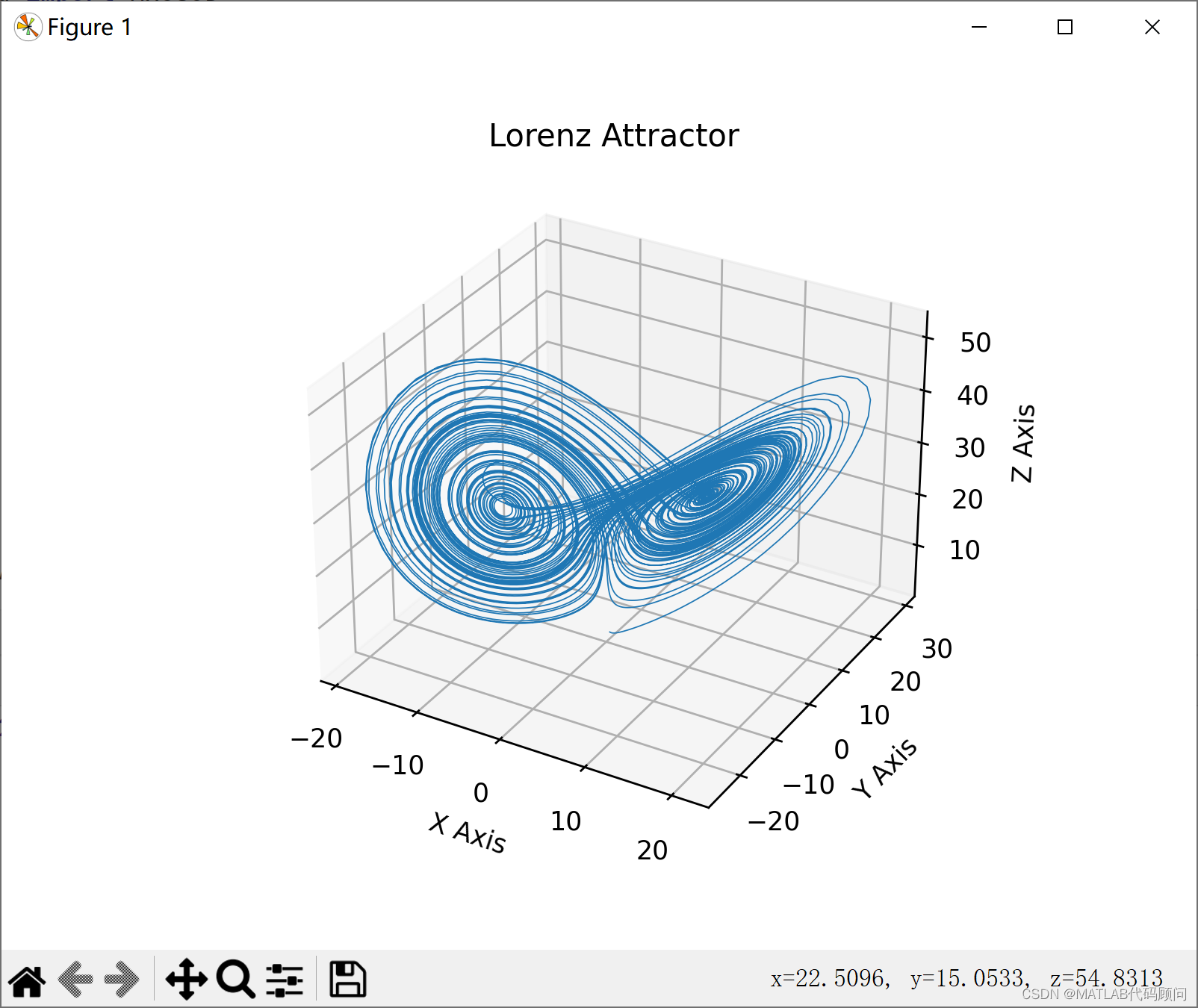








 本文介绍了蝴蝶曲线(洛伦兹吸引子),一种与混沌理论紧密相关的概念,通过Python代码展示了如何使用洛伦兹方程模拟并可视化这种系统的长期行为,强调了初始条件微小变化可能导致结果的巨大差异。
本文介绍了蝴蝶曲线(洛伦兹吸引子),一种与混沌理论紧密相关的概念,通过Python代码展示了如何使用洛伦兹方程模拟并可视化这种系统的长期行为,强调了初始条件微小变化可能导致结果的巨大差异。


















 1074
1074

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










