(一)基础数学知识
随机变量的协方差
在概率论和统计中,协方差是对两个随机变量联合分布线性相关程度的一种度量。两个随机变量越线性相关,协方差越大,完全线性无关,协方差为零。定义如下。
cov(X,Y)=E[(X−E[X])(Y−E[Y])]
当 X, Y是同一个随机变量时, X与其自身的协方差就是 X的方差,可以说方差是协方差的一个特例。或
η,取值范围为[-1,1],越接近1表示这两个随机变 量的相关性越大,越接近-1表示这两个随机变量的相关性越小。
样本的协方差
在实际中,通常我们手头会有一些样本,样本有多个属性,每个样本可以看成一个多维随机变量的样本点,我们需要分析两个维度之间的线性关系。协方差及相关系数是度量随机变量间线性关系的参数,由于不知道具体的分布,只能通过样本来进行估计。
设样本对应的多维随机变量为 ,样本集合
,样本集合 ,
,
m为样本数量。与样本方差的计算相似,a和b两个维度样本的协方差公式为 ,
,
这里分母为m-1是因为随机变量的数学期望未知,以样本均值代替,自由度减一。
向量的表示及基变换
内积: 

令B为单位向量,则A与B的内积值等于A向B所在直线投影的矢量长度

向量的表示及基变换
基的定义:一个向量空间,存在一个线性无关的向量组x1,...xn,...,使得对所有空间中的向量,都能被这个组线性表示.这个向量组就是这个空间的基.如果这个无关组有无限个向量,那么称这个空间是无限维的,如果有k个向量就称是k维的.
一般的,在n维空间中,那单位n个单位向量能构成一个基.但,基不是唯一的,任何个数为n的线性无关向量组都能构成n维空间的一基.
若向量为(3,2),实际上表示线性组合:  ,(1,0)和(0,1)叫做二维空间中的一组基.
,(1,0)和(0,1)叫做二维空间中的一组基.


基变换:数据与一个基做内积运算,结果作为第一个新的坐标分量,然后与第二个基做内积运算,结果作为第二个新坐标的分量
如向量(3,2)映射到基中坐标

(二)主成分分析
下面以一个例子说明主成份分析的步骤
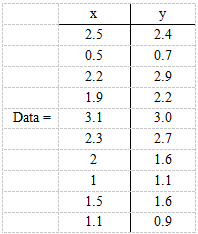
现在假设有一组数据如下:
行代表了样例,列代表特征,这里有10个样例,每个样例两个特征。可以这样认为,有10篇文档,x是10篇文档中“learn”出现的TF-IDF,y是10篇文档中“study”出现的TF-IDF。
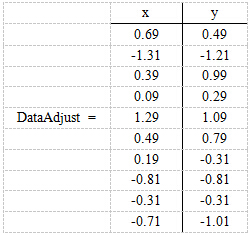
第一步,对数据进行中心化:分别求x和y的平均值,然后对于所有的样例,都减去对应的均值。这样是为了使每个特征的数据均值为零。简化方差和协方差矩阵的计算。此时方差公式为:
 ,均值
,均值 为零。协方差公式为
为零。协方差公式为
 ,m为样本的个数。协方差矩阵为(X^T)X
,m为样本的个数。协方差矩阵为(X^T)X
这里x的均值是1.81,y的均值是1.91,那么一个样例减去均值后即为(0.69,0.49),得到
第二步,求特征协方差矩阵,如果数据是3维,那么协方差矩阵是
这里只有x和y,求解得
对角线上分别是x和y的方差,非对角线上是协方差。协方差是衡量两个变量同时变化的变化程度。协方差大于0表示x和y若一个增,另一个也增;小于0表示一个增,一个减。如果x和y是统计独立的,那么二者之间的协方差就是0;但是协方差是0,并不能说明x和y是独立的。协方差绝对值越大,两者对彼此的影响越大,反之越小。协方差是没有单位的量,因此,如果同样的两个变量所采用的量纲发生变化,它们的协方差也会产生树枝上的变化。
第三步,求协方差的特征值和特征向量,得到
上面是两个特征值,下面是对应的特征向量,特征值0.0490833989对应特征向量为,这里的特征向量都归一化为单位向量。
第四步,将特征值按照从大到小的顺序排序,选择其中最大的k个,然后将其对应的k个特征向量分别作为列向量组成特征向量矩阵。
这里特征值只有两个,我们选择其中最大的那个,这里是1.28402771,对应的特征向量是(-0.677873399, -0.735178656)T。
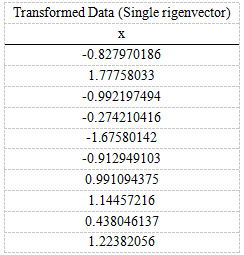
第五步,将样本点投影到选取的特征向量上。假设样例数为m,特征数为n,减去均值后的样本矩阵为DataAdjust(m*n),协方差矩阵是n*n,选取的k个特征向量组成的矩阵为EigenVectors(n*k)。那么投影后的数据FinalData为
FinalData(10*1) = DataAdjust(10*2矩阵) x 特征向量(-0.677873399, -0.735178656)T
得到的结果是
这样,就将原始样例的n维特征变成了k维,这k维就是原始特征在k维上的投影。
再看一个例子:以下数据由五个有两个特征的样本组成,将其从二维变为一维。

整个PCA过程貌似及其简单,就是求协方差的特征值和特征向量,然后做数据转换。但是有没有觉得很神奇,为什么求协方差的特征向量就是最理想的k维向量?
这位老哥写的很好,推荐阅读:点击打开链接
.
是因为随机变量的数学期望未知,以样本均值代替,自由度减一。
包含的信息量呢? 一个基(basis)一个基地衡量. 数据集在某个基上的投影值(也是在这个基上的坐标值)越分散, 方差越大, 这个基保留的信息也就越多. 不严格的来一句, 一个基集保留下的信息量是每个基保留下的信息量的和.
基于上面的理念, 或者说假设, 我们已经有一种可以有效地找出最优基集的方法了: 贪心算法---先找出保留信息量最大的基向量, 然后是第二大的, 然后然后, 直到找满pp个基向量.
接下来, 将上面的分析用数学语言描述出来.








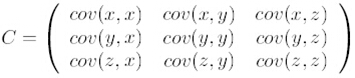
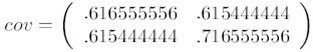
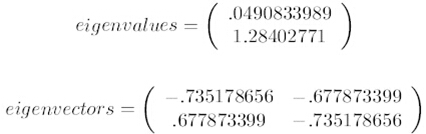














 1万+
1万+











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








