Hilbert排序

  Hilbert排序

 

陈玉进 李泉 南京跬步科技有限公司（http://www.creable.cn）

 

一维索引已经非常成熟了，折半查找（二分查找）是我们最熟悉的线性索引查找方式，数据库中常用的B树索引，也是一种高效的一维索引，一维索引之所以容易解决是因为数据是可以“严格”线性排序的，就如同一维数轴上的数有严格的前后顺序，而二维平面，就不存在像一维数组那样严格的前后顺序一说，只能根据具体需要具体给定排序的定义，这个问题的本质就是二维到一维的映射排序，即n=f(x,y)。如二维数组是按行排列的，每个数组位置（x,y），对应一个序号，内外存其实是一维存储器，存在这种映射关系。

 

基于Hilbert填充曲线的二维排序，是另一种排序方式，如图是一、二、三阶填充曲线，它是延填充曲线经过格网的先后顺序来排列的，这种排序的最大特点——空间聚簇，所谓“空间聚簇”，就是空间上靠得近的网格，Hilbert排序后生成的序号也尽量靠近，而二维数组按行排序空间聚簇性较差。

 

 

 

 

 

空间聚簇有什么优点呢?下面来谈谈在GIS中的用途：地图显示时，空间上之间靠得近的要素被一起读取显示的概率大于之间离得远的要素，所以，靠得近的要素物理上靠近存储，这样就减少了计算机I/O读取外存的次数和寻道时间（I/O的存取单元是一个物理磁盘块），提高系统的性能，所以，Hilbert排序在GIS数据物理存储中有着重要的应用，线性可排序四叉树索引就是Hilbert排序的典型应用，这个将在后面的章节详细介绍。

 

具体用算法怎么实现Hilbert排序呢？关键是用算法生成出Hilbert填充曲线，经典算法有：面向字节技术方法、几何方法、L系统方法、IFS迭代函数系统方法等，由于这些算法大都是对曲线的每条线段逐渐细分做递归计算, 每次运算粒度小, 当迭代次数较大时计算非常耗时，因此, 有必要研究大粒度的迭代算法，这里我们采用陈宁涛等提出的方法，采用“矩阵复制、翻转、迭代”的思想，解决大型Hilbert填充曲线生成的效率问题。下面详细介绍这个算法的思路（Hilbert填充曲线，要求网格单元个数是2^n×2^n，刚好与四叉树的要求一致，如果不符合这个条件，可以通过扩充网格的方法）。

 

 

 

 

 

 

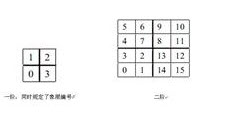
如图，我们观察Hilbert填充曲线是如何从一阶生成二阶的，二阶又如何生成三阶的，等等如此迭代下去。这里我们只要看一阶如何生成二阶的，即如何由4个网格生成出16个网格的，下面按同样的方法迭代即可。我们先约定一下，四个网格的象限编号。

  

 

在二阶中，第1象限的四个网格是一阶对应的四个网格值加上4，即1×4；第2象限的四个网格是一阶对应的四个网格值加上8，即2×4；第3象限的四个网格值——首先把一阶中的四个网格作转置运算，即按正对角线互换，然后把一阶中置换后的四个网格加上12，即3×4；第0象限的四个网格是一阶对应的四个网格按“斜对角线”置换而