数学建模基本算法模型Chapter1--线性规划

数学建模基本算法模型Charpter1–线性规划（LP）

By 进栈需检票

一、线性规划基本概念

1.Linear Programming （LP问题）

列出方程组不等式求解（基本形式）

包含目标函数以及约束条件

目标函数及约束条件均为线性函数，故称为线性规划问题，目标是求解目标函数最大最小的问题

关键：如何吧问题归结成一个线性规划问题，以及模型的构建是否恰当，这就需要找到合适的决策变量

Attention：前面的s.t.就是约束条件的意思，在论文中间写出来表示其专业性

a.可行解：满足约束条件（4）的解
$$x=[x_1,L,x_n{]}^T$$
b.最优解：使得目标函数（3）达到最大值的可行解成为最优解

c.可行域：所有可行解构成的集合称为问题的可行域，记作R

2.应用情况

注意：“线性”意味着所有的变量都是一次方

超过一次方就属于非线性规划

①“怎么安排/分配”、“尽量多（少）”、“最多（少）”、“利润最大”、“最合理”

②生产安排：原材料、设备有限制、总利润最大

③投资收益：资产配置、收益率、损失率、组合投资、总收益最大（总收益率则不是线性规划）

④销售运输：产地、销量、产量、销量、运费、总运费最省

⑤车辆安排：路线、起点终点、承载量、时间点、车次安排最合理

⑥还有的就是整数规划和0-1规划，往往默认为线性规划问题

二、Matlab的线性规划标准以及软件求解

1.功能简介

“虽然Matlab自带函数，但是你必须将数据化成其支持的形式，例如，只求最小值不能直接求最大值，要求最大值则将数据整理为 负数然后求负数的最小值，绝对值后则是原目标函数的最大值”

同样的，只支持小于等于和等于，若是大于等于则一样的要化作负数进行计算转化

（价值向量为f，minf^Tx）

资源向量：问题资源（金钱）的总和，也就是最关键的限制因素

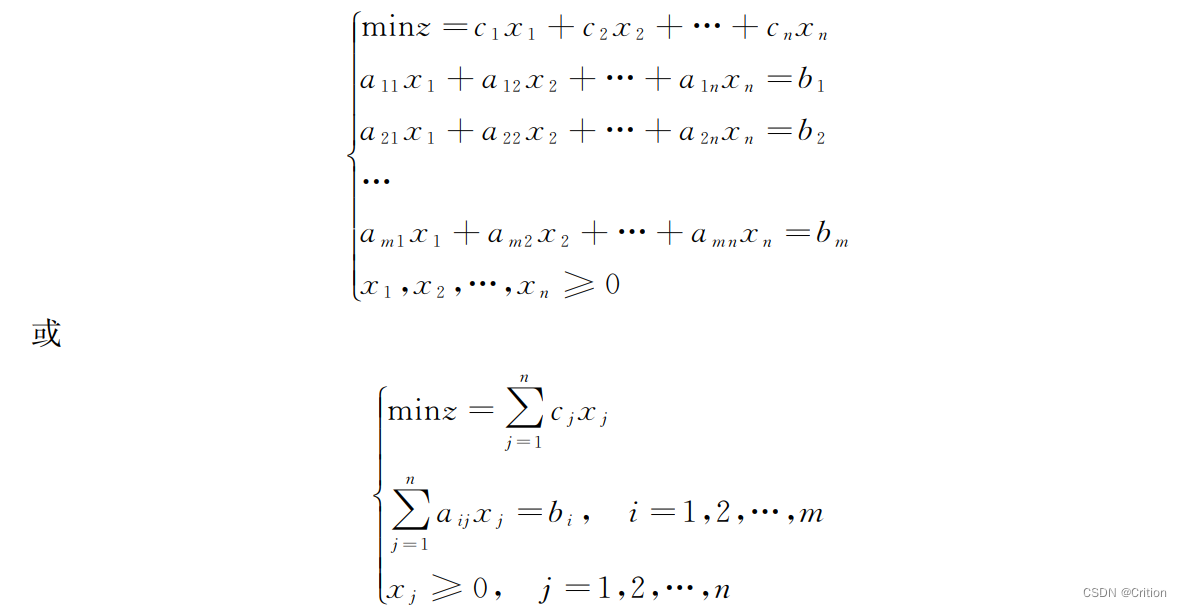
(1)每个模型都有若干个决策变量(x1,x2,x3,…,xn), 其中n 为决策变量个数。决策变量的一组值表示一种方案,同时决策变量一般是非负的。

(2)目标函数是决策变量的线性函数,根据具体问题可以是最大化(max)或最小化 (min),二者统称为最优化(opt)。

(3)约束条件也是决策变量的线性函数。

2.函数功能介绍

$$[x,fvla]=linprog(f,A,b,Aeq,beq,lb,ub)$$

x返回的最优解为变量范围，fval返回的目标函数的最优解

f价值向量，为列向量

A不等式约束条件的变量系数矩阵，b不等式约束条件的常数项矩阵

Aeq等式约束条件的系数矩阵，beq等式约束条件的常数项矩阵

lb决策变量的最小值 ub决策变量的最大值（自变量的取值范围）

使用特例：

①若不存在不等式约束，用[ ]来代替A与b
$$[x,fval]=linprog(f,[],[],Aeq,beq,lb,ub)$$
②若不存在等式约束，用[ ]来代替Aeq与beq
$$[x,fval]=linprog(f,A,b,[],[],lb,ub)$$
③没有等式约束和最大最小的取值约束的时候，可以不写Aeq，beq，lb以及ub
$$[x,fval]=linprog(f,A,b)$$
④若求最大值，先取负号得出结论之后再去绝对值得到正确的最大值解

三、简单的使用案例

1.单纯形线性规划

Example1 – 简单的线性回归1

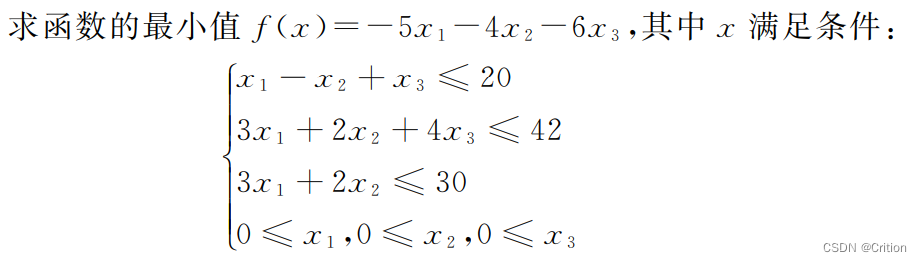
f = [-5 , -4 , -6];
A = [1 -1 1
     3 2 4
     3 2 0];
b = [20 , 42 , 30];
lb = [0 , 0 , 0];
ub = [inf , inf , inf];
Aeq = [];
beq = [];
[x , fval] = linprog(f , A , b , Aeq , beq , lb , ub);
x
fval

输出结果：

Optimal solution found.


x =

         0
   15.0000
    3.0000


fval =

   -78

Example2 – 简单的线性回归（zeros(3 , 1)）

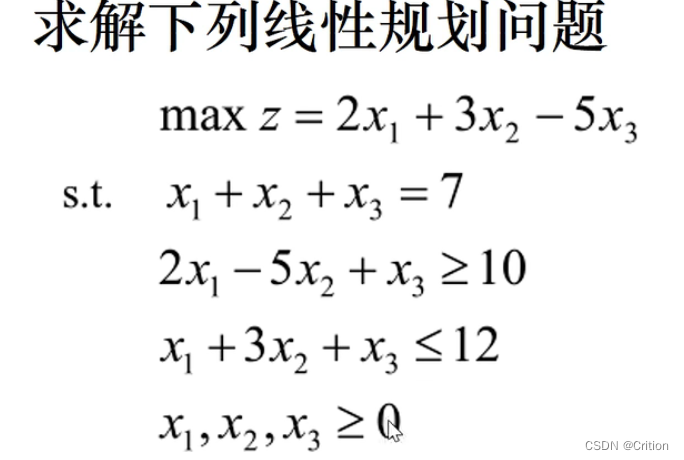
对于求这个max，记得f一定要求负数的形式，以及后面的A，Aeq，以此类推

f = [-2 , -3 , 5];
A = [-2 5 -1
     1  3  1];
b = [-10 , 12];
Aeq = [1 , 1 , 1];
beq = 7;
ub = [inf , inf , inf];
lb = [0 , 0 , 0];
[x , fval] = linprog(f , A , b , Aeq , beq , lb , ub);
x
fval
-fval

当然，对于后面的lb，我们还可以写成zeros(3 , 1)
也就是三行一列的行列式中的元素全部为0，其实也就是
$$lb{x}_1=0,lb{x}_2=0,lb{x}_3=0$$
ub = inf，在函数中可以忽略或者用[ ]代替使用

也就是：

[x , fval] = linprog(f , A , b , Aeq , beq , zeros(3 , 1));

Example3 – 方程整体优化问题之[x,fval,exitflag,output,lambda]=linprog(…)

■ [x,fval,exitflag]=linprog(…)———返回exitflag值,描述函数计算的退出条件。
■ [x,fval,exitflag,output]= linprog(…)———返 回 包 含 优 化 信 息 的 输 出 变 量 output。
■ [x,fval,exitflag,output,lambda]=linprog(…)———将解x处的 Lagrange乘子返 156 回到lambda参数中。

clear all
f = [-5 , -4 , -6];
A = [1 -1 1
     3 2  4
     3 2  0];
b = [20 , 42 , 30];
Aeq = [ ];
beq = [ ];
lb = zeros(3 , 1);
ub = [inf , inf , inf];
[x , fval , exitflag , output , lamba] = linprog(f , A , b , Aeq , beq , lb , ub);
x
fval
exitflag
output
lamba

exitflag = 1表示过程正常收敛于解x 处。

Example4 – 绝对值问题的线性规划转化思考

貌似不是线性规划问题，但是可以通过相关的代数变换来使其成为所谓的线性规划问题

Example5 – 线性规划在金融分析的实际问题

基本概况：

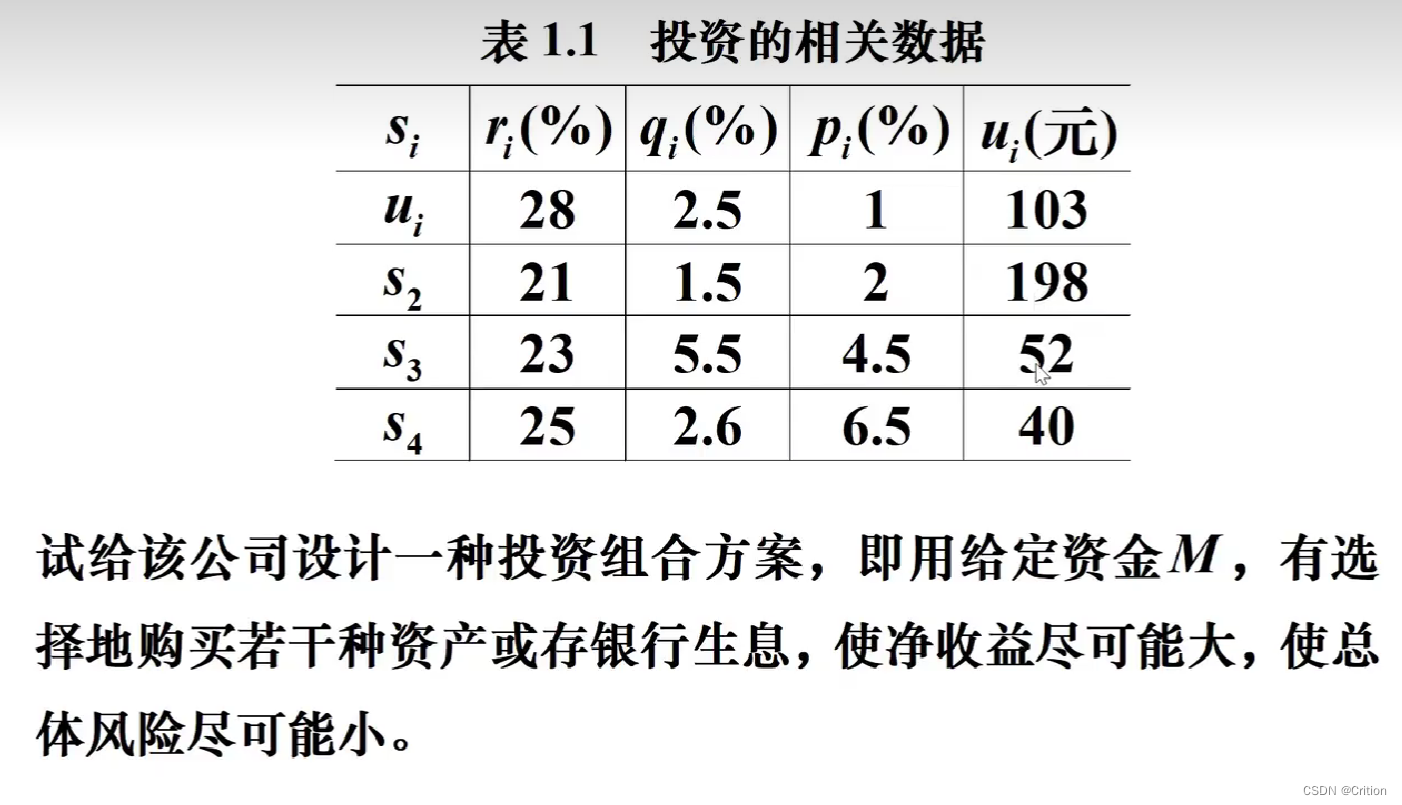
①首先，来一波符号定义

②然后来个基本假设

在这里的假设也是很重要的，比如（4）这个独立性问题，假如没有在这路单独提出来，评委可能就会在这个点上去提问，所以，完备的假设是成功的前提以及后续实验的逻辑支撑

这些逻辑包括基本逻辑，类似（2）以及这个研究问题的操作性假设，例如（5）（6）这些影响结果和计算精确度的因素

③模型的构建

首先需要确定题目的已知条件

同时，由题目所知，总体风险是是可用投资Si中最大的那一个
m a x { q i x i   ∣   i = 1 , 2 , L , n } max\{q_ix_i\ |\ i = 1,2,L,n\} max{qi​xi​ ∣ i=1,2,L,n}

通过分析（u_i的值不受影响），我i们分析出净收益率：
$$(r_i-p_i)x_i$$

然后就是分析现有的题目目标

也就是让收益尽可能大，总体风险尽可能小

这是一个多目标的线性规划问题

得出目标函数以及约束条件！！！

目标函数：

此所谓收益尽可能大
$$max\sum _{i=0}^n(r_i-p_i)x_i$$
此所谓总体风险 尽可能小
m i n ( m a x { q i x i } ) min(max\{q_ix_i\}) min(max{qi​xi​})
约束条件：
$$\sum _{i=0}^n(1+p_i)x_i=M$$

$$x_i\ge 0,i=0,1,L,n$$

进行模型的分析、列举以及筛选

这里的模型将我们原型中的min(max{qixi})进行了转化，通过一个风险率qixi/M来进行相应的约束，这样做不仅让评委能够更好的理解，同时也让整个模型分析的水平上了一个台阶

同样的，在模型二中，淡化了风险，增强了收益这个目标

模型一模型二的转化其实就是将两个目标函数（多目标的线性规划）中的一个或者多个转化到约束条件，进行模型的简化以及可能性的提升

两个变量不是不可以求解，而是根据不同的实际情况进行分别的分析理解计算建模

模型三就是两种变量情况都算在考虑之中，赋予不同的权重来表示其实际情况

变量的综合分析以及使用才是思考的重点

模型三是推荐的一种建模方式

将模型计算翻译为Matlab的理解形式

#模型一

代码书写构建

#模型一

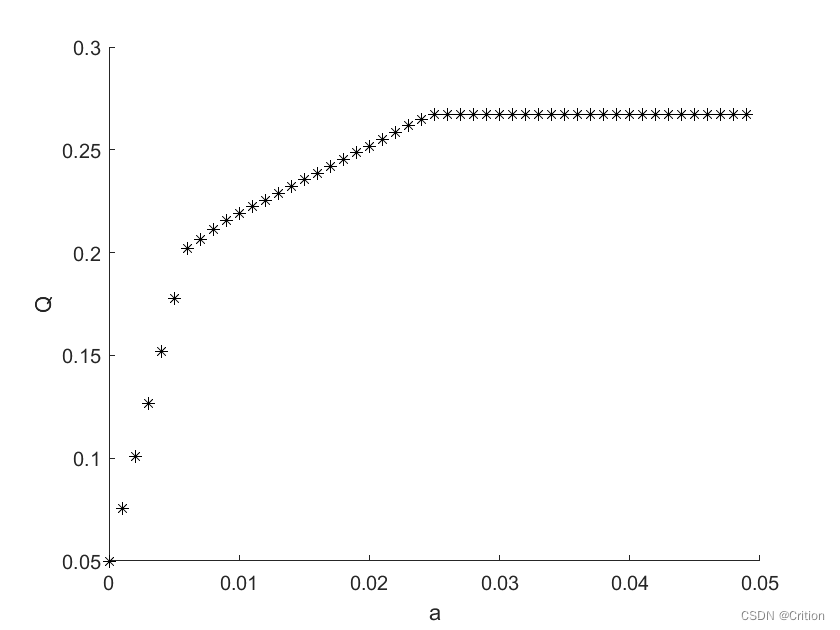
a = 0;
hold on
while a < 0.05
    f = [-0.05 , -0.27 , -0.19 , -0.185 , -0.185];
    A = [zeros(4 , 1) , diag([0.025 , 0.015 , 0.055 , .026])];
    b = a * ones(4 , 1);
    Aeq = [1 , 1.01 , 1.02 , 1.045 , 1.065];
    beq = 1;
    LB = zeros(5 , 1);
    [x , Q] = linprog(f , A , b , Aeq , beq , LB);
    Q = -Q;
    plot(a , Q , '*k');
    a = a + 0.001;
end
xlabel('a') , ylabel('Q')

得出结论

#模型一

2.多目标线性规划

目标线性规划：
$$max\mathbf{Z}=\mathbf{C}x$$
约束条件：
$$\mathbf{A}x\le b$$

$$x\ge 0$$

1.理想点法

所以在这样的题目条件下做题的顺序就是先把一个个情况的求解出来，之后就是用minw[Z(x)]去求得真正的解，使用Matlab中的fmincon

Example6

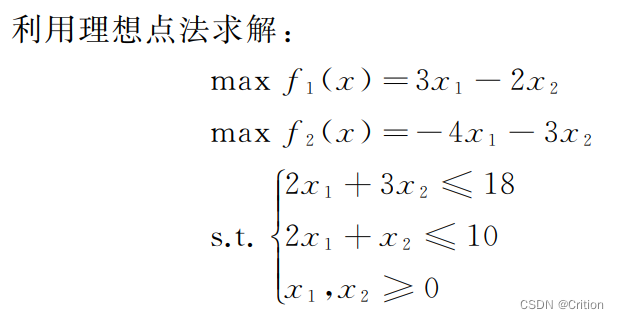
①求解f1(x)最优解

clear all
clc
f= [3 , -2]; 
A= [2 3 
    2 1];    
b= [18 , 10];
lb= [0 , 0];
[x , fval] =linprog(f , A , b , [ ] , [ ] , lb);
x
fval

------------
Output

x =
	0.0000
	6.0000
fval =
	-12.0000

即最优解为12

②求解f2(x)最优解

f = [-4 , -3];
A = [2 , 3
     2 , 1];
b = [18 , 10];
lb = [0 , 0];
[x , fval] = linprog(f , A , b , [ ] , [ ] , lb);
x
fval

------------
Output

x =
	3.0000
	4.0000
fval =
	-24.0000

即最优解为24

③综合公式求解该模型的最优解

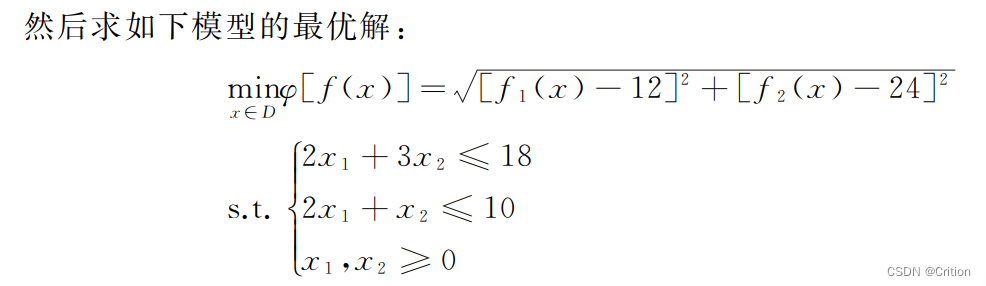
A = [2 , 3
     2 , 1];
b = [18 , 10];
lb = [0 , 0];
x0 = [1 , 1];
x = fmincon('((-3*x(1)+2*x(2)-12)^2+(4*x(1)+3*x(2)-24)^2)^(1/2)' , x0 , A , b , [ ] , [ ] , lb , [ ]);
x

------------
Output
x =
	0.5268
	5.6488

这样求出来的x1 , x2就是满足以上两个条件的最优解了

2.线性加权和法

相较于理想点法的不同，这个方法注重于题目给的目标函数是基于一个权重分配的形式。

Example7

f = [-0.5 , -2.5];
A = [2 , 3
     2 , 1];
b = [18 , 10];
lb = [0 , 0];
x = linprog(f , A , b , [ ] , [ ] , lb);
x

------------
Output
x =
	0.0000
	6.0000

其实就是两个或多个函数根据一定的权重比例组合到一个目标函数里面，再使用linprog函数进行求解，过程与单纯性线性规划一致

3.最大最小法

例如Example5的目标函数的构建

Example8

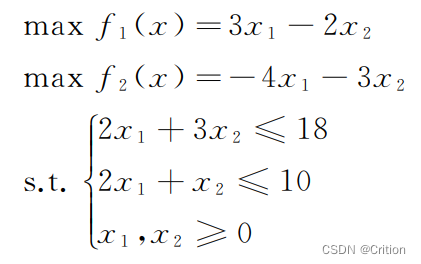
使用最大最小法求解

f函数.m文件

function f = crition2022(x)
f(1) = 3*x(1) - 2*x(2);
f(2) = -4x*(x) - 3*x(2);

求解的程序

clear all
clc
x0 = [1 , 1];
A = [2 , 3
     2 , 1];
b = [18 , 10];
lb = zeros(2 , 1);
[x , fval] = fminimax('crition2022' , x0 , A , b , [ ] , [ ] , lb , [ ]);
x
fval

------------
Output
x =
	0
	6
fval =
	-12 	-18