【JZOJ5260】【GDOI2018模拟8.12】区间第k小

Description

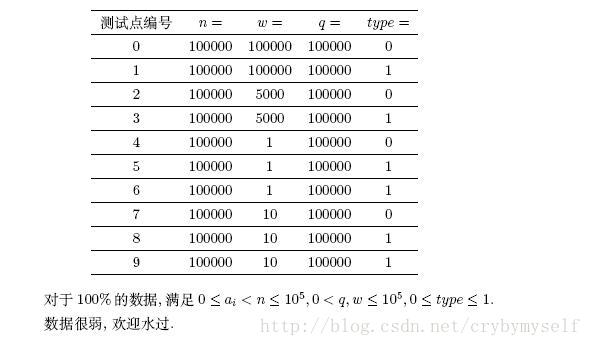
Data Constraint

Solution

我们先考虑离线做法。显然是莫队+数据结构。但我们发现莫队是插入$N\sqrt N$次查询n次，那么用线段树维护十分不划算，所以我们考虑提高查询复杂度而降低插入复杂度。于是我们想到了分块。我们对数值分为根号块，维护块内每个数出现次数和答案。那么单次插入O(1)，单次查询O（$\sqrt N$),总时间复杂度O($N\sqrt N$)。
那么在线呢?我们沿用离线的分块想法。将序列分为根号个块，设ans[i][j][k]表示序列i块到j块上数值在按数值分块的第k块上的满足出现次数不大于w的数的数量，sum[i][j]表示值i在序列前j块出现的次数。ans[i][j][k]可以通过枚举块i，然后枚举i块及其往后的序列，当一个数x出现次数大于w时，我们在其所属的ans[i][j][k]减去其总共出现的次数并将其赋值为-1，保证往后不会再计算，接下来只用ans[i][j][k]加上ans[i][j-1][k]即可抵消x在ans[i][j][k]的贡献。sum[i][j]维护十分简单就不讲了。
我们考虑如何求答案。对于一个询问[l,r]我们可以知道完全被[l,r]包含的块[i,j]的大致答案ans[i][j]，但我们还需考虑不在块内的剩余数。我们统计不在块内的数的数量，如某些数x在块[i~j]内出现次数不大于w，而加上不在块内的数量后大于w，我们将其在ans[i][j][k]中减去它的贡献。反之则加上它的贡献。最后我们枚举答案所在的块k，对答案所在的块内暴力计算答案的值即可。时间复杂度O((N+Q)$\sqrt N$)。

Code

#include<iostream>
#include<cmath>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int maxn=1e5+5,maxn1=320,maxn2=1e5;
int ans[maxn1][maxn1][maxn1],sum[maxn][maxn1],a[maxn],r[maxn],bz[maxn],bz1[maxn],b[maxn],rr[maxn];
int n,m,i,t,j,k,l,x,y,z,bz2,p,ln,q,ans1,test,ln1,qq,num,num1;
void dg(int x,int y){
    int z=0;
    for (j=x;j<=y;j++)
        if (sum[a[j]][k]-sum[a[j]][t-1]<=m){
            p=a[j]/qq+1;
            if (sum[a[j]][k]-sum[a[j]][t-1]+bz[a[j]]>m)ans[t][k][p]-=sum[a[j]][k]-sum[a[j]][t-1];
            else ans[t][k][p]+=bz[a[j]];
            bz[a[j]]=0;
        }
}
void dg1(int x,int y){
    for (j=x;j<=y;j++)
        if (sum[a[j]][k]-sum[a[j]][t-1]<=m){
            p=a[j]/qq+1;
            if (sum[a[j]][k]-sum[a[j]][t-1]+bz1[a[j]]>m)ans[t][k][p]+=sum[a[j]][k]-sum[a[j]][t-1];
            else ans[t][k][p]-=bz1[a[j]];
            bz1[a[j]]=0;
        }
}
int main(){
    freopen("kth.in","r",stdin);freopen("kth.out","w",stdout);
    scanf("%d%d%d%d",&n,&m,&test,&bz2);
    ln=sqrt(n);q=ln;ln1=sqrt(maxn2);qq=ln1;
    for (i=1;i<=n;i++)scanf("%d",&a[i]);
    for (i=1;i<=ln;i++) r[i]=i*ln;
    for (i=1;i<=ln1;i++) rr[i]=i*ln1-1; 
    r[++ln]=n;rr[++ln1]=maxn2;rr[0]=-1;
    for (i=1;i<=ln;i++){
        for (j=0;j<=maxn2;j++)
            sum[j][i]=sum[j][i-1];
        for (j=r[i-1]+1;j<=r[i];j++)
            sum[a[j]][i]++;
    }
    for (i=1;i<=ln;i++){
        k=i;memset(bz,0,sizeof(bz));
        for (j=r[i-1]+1;j<=n;j++){
            if (bz[a[j]]>=0){
                bz[a[j]]++;t=a[j]/qq+1;
                ans[i][k][t]++;
                if (bz[a[j]]>m){
                    ans[i][k][t]-=bz[a[j]];
                    bz[a[j]]=-1;
                }
            }
            if (j==r[k]) k++;
        }
        for (j=i+1;j<=ln;j++)
            for (k=1;k<=ln1;k++)
                ans[i][j][k]+=ans[i][j-1][k];
    }
    memset(bz,0,sizeof(bz));
    for (i=1;i<=test;i++){
        scanf("%d%d%d",&x,&y,&z);x^=bz2*ans1;y^=bz2*ans1;z^=bz2*ans1;
        t=x/q+(x%q!=0)+(x%q!=1);
        if (y!=r[ln]) k=y/q-(y/q==ln && y!=ln*q);
        else k=ln;
        if (t>k){
            b[0]=0;
            for (j=x;j<=y;j++)bz[a[j]]++;
            for (j=x;j<=y;j++)if(bz[a[j]]<=m) b[++b[0]]=a[j];
            if (b[0]>=z){
                sort(b+1,b+b[0]+1);
                printf("%d\n",b[z]);ans1=b[z];
            }else printf("%d\n",n),ans1=n;
            for (j=x;j<=y;j++)bz[a[j]]=0;
        }else{
            for (j=x;j<=r[t-1];j++)bz[a[j]]++,bz1[a[j]]++;
            for (j=r[k]+1;j<=y;j++)bz[a[j]]++,bz1[a[j]]++;
            dg(x,r[t-1]);dg(r[k]+1,y);
            num=0;
            for (j=1;j<=ln1;j++){
                if (num+ans[t][k][j]<z) num+=ans[t][k][j];
                else{
                    for (l=rr[j-1]+1;l<=rr[j];l++)
                        if (sum[l][k]-sum[l][t-1]+bz1[l]<=m){
                            if (num+sum[l][k]-sum[l][t-1]+bz1[l]<z) num+=sum[l][k]-sum[l][t-1]+bz1[l];
                            else{
                                num=-1;
                                printf("%d\n",l);
                                ans1=l;
                                break;
                            }
                        }
                    break;
                }
            }
            if (num>=0) printf("%d\n",n),ans1=n;
            dg1(x,r[t-1]);dg1(r[k]+1,y);
            for (j=x;j<=r[t-1];j++)bz[a[j]]=bz1[a[j]]=0;
            for (j=r[k]+1;j<=y;j++)bz[a[j]]=bz1[a[j]]=0;
        }
    }
}