python数据分析-线性代数基础

大家好，今天我们用python语言去实现线性代数的一些基础计算等，常用第三方NumPy库来实现线性代数的计算。

线性代数是一门应用性很强但理论非常抽象的数学学科，是与数据分析紧密相关的数学科目，其中的很多定理、性质和方法在数据分析中起到了关键性的作用。

一、行列式

使用NumPy库中linalg模块的det函数可以求解行列式，其语法格式如下：

numpy.linalg.det(a)
#a:接受 array,表示需要进行求解的行列式。无默认值

利用行列式求解线性方程组，可使用NumPy库中linalg模块的solve函数实现，其语法格式如下：

numpy.linalg.solve(a,b)
# a:接受 array,表示需要进行求解的方程组的系数行列式。无默认值
# a:接受 array,表示需要进行求解的方程组的"因变量"值。无默认值

实例一：某企业为丰富职工的业余文化生活，组织职工去影院看电影，花了2050元买了80张电影票，其中，单价为30元的甲级票有x1张，单价为20元的乙级票有x2张，求x1和x2，求某数据的众数，建立方程：x1+x2=80；30x1+20x2=2050。

import numpy as np#导入库Numpy
#方法一，使用det()函数求行列式
arr = np.array([[1,1],[30,20]]) #创建分母的二维数组
arr1 = np.array([[80,1],[2050,20]]) #创建分子的二维数组
arr2 = np.array([[1,80],[30,2050]]) #创建分子的二维数组
#求解行列式
D = np.linalg.det(arr)
D1 = np.linalg.det(arr1)
D2 = np.linalg.det(arr2)
print('方法一：方程组的解x1，x2分别为：',D1/D,D2/D)
#方法二，使用solve()函数求行列式
y = np.array([80,2050])
x = np.linalg.solve(arr,y)
print('方法二：方程组的解为：',x)

输出结果：

方法一：方程组的解x1，x2分别为：44.99999999999996 35.000000000000014
方法二：方程组的解为：[45. 35.]

实例二：计算三阶行列式[4 6 8；4 6 9; 5 6 8]

import numpy as np#导入库Numpy
arr = np.array([[4,6,8],[4,6,9],[5,6,8]]) #创建三阶行列式
print('行列式的值为：',np.linalg.det(arr))

结果输出：

行列式的值为：5.999999999999998

二、逆序数

在一个排列中，如果某两个元素的前后位置与自然顺序相反，即前面的数大于后面的数，那么称这两个元素构成一个逆序。一个排列中所有逆序的总个数称为这个排列的逆序数。

实例：对于排列42531，计算每一个元素左侧比其大的元素的个数，再求和，具体如下：

import numpy as np#导入库Numpy
def amount(b):
    #计算 b中大于第i个元素的总个数
    counts = [np.sum(b[:i]>bb) for i,bb in enumerate(b)]
    return np.sum(counts)
a = np.array([4,2,5,3,1])
print('逆序数为：',amount(a))

输出结果：

逆序数为：7

三、 行列式的转置

import numpy as np#导入库Numpy
D = np.array([[4,6,8],[4,6,9],[5,6,8]]) #创建行列式
DT = D.T #创建行列式的转置行列式

四、 矩阵

4.1 创建矩阵

创建矩阵有两种方法，使用mat函数和matrix函数。

import numpy as np#导入库Numpy
#方法一
A1 = np.mat('1 2 3 4;3 4 5 6;5 6 7 8;7 8 9 0')
print('使用mat函数创建的矩阵为：\n',A1)
# 方法二
A2 = np.matrix([[1,2,3,4],[3,4,5,6],[5,6,7,8],[7,8,9,0]])
print('使用matrix函数创建的矩阵为：\n',A2)

结果输出：

使用mat函数创建的矩阵为：
 [[1 2 3 4]
 [3 4 5 6]
 [5 6 7 8]
 [7 8 9 0]]
使用matrix函数创建的矩阵为：
 [[1 2 3 4]
 [3 4 5 6]
 [5 6 7 8]
 [7 8 9 0]]

4.2 零矩阵

设有矩阵，若其所有元素均为0，则称其为零矩阵，记为O。

使用NumPy库中的zeros函数可以创建零矩阵，其语法格式如下：

numpy.zeros(share,dtype=float,order='C')
# shape:接收int或int序列，表示数组的形状。无默认值

在Python中使用两种方法创建3行3列的单位矩阵：

import numpy as np#导入库Numpy
o = np.zeros((3,3))
print('零矩阵o为：\n',o)

结果输出：

零矩阵o为：
 [[0. 0. 0.]
 [0. 0. 0.]
 [0. 0. 0.]]

4.3 单位矩阵

设有n阶方阵，其主对角线上的元素均为1，其余元素全为0，则称其为n阶单位矩阵，记为E或I。

使用NumPy库中的identity函数或eye函数可以创建单位矩阵，其语法格式如下：

numpy.identity(n,dtype=None)
# n:接收 int，表示输出n行n列的矩阵。无默认值
numpy.eye(N,M=None,k=0,dtype=<class 'float'>)
# N:接收int，表示输出的行数。无默认值
# k:接收int，表示主对角线的索引。默认为0

在Python中使用两种方法创建3行3列的单位矩阵：

import numpy as np#导入库Numpy
E = np.identity(3) #使用identity函数创建3行3列矩阵
print('单位矩阵E为：\n',E)
I = np.eye(3,k=0) #使用eye函数创建3行3列矩阵
print('单位矩阵E为：\n',I)

结果输出：

单位矩阵E为：
 [[1. 0. 0.]
 [0. 1. 0.]
 [0. 0. 1.]]
单位矩阵E为：
 [[1. 0. 0.]
 [0. 1. 0.]
 [0. 0. 1.]]

4.4 对角矩阵

其非主对角线上的元素均为0，则称A为对角矩阵，记为A=diag（λ1，λ2，…，λn）。

使用NumPy库中的diag函数可以创建对角矩阵，其语法格式如下：

numpy.diag(v,k=0)
# v:接收array或list，表示输入的数据。无默认值
# k:接收int，表示主对角线的索引。默认为0

在Python中创建4行4列的对角线矩阵A：

import numpy as np#导入库Numpy
A = np.diag([1,2,3,4],k=0)
print('对角矩阵A为：\n',A)

结果输出：

对角矩阵A为：
 [[1 0 0 0]
 [0 2 0 0]
 [0 0 3 0]
 [0 0 0 4]]

五、 矩阵的运算

5.1 矩阵的乘法

使用NumPy库中的dot函数可以实现矩阵的乘法计算，其语法格式如下：

numpy.dot(a,b,out=None)
# a:接收array或matrix，表示第一个乘数。无默认值
# b:接收array或matrix，表示第二个乘数。无默认值

求矩阵的乘法：

import numpy as np#导入库Numpy
A = np.matrix([[1,2,3],[1,1,2],[0,1,2]])
B = np.matrix([[16,25],[20,8],[15,14]])
print('方法一：',A*B)
print('方法二：',np.dot(A,B))

结果输出：

方法一：[[101  83]
 [ 66  61]
 [ 50  36]]
方法二：[[101  83]
 [ 66  61]
 [ 50  36]]

5.2 矩阵的转置

import numpy as np#导入库Numpy
A = np.matrix([[1,2,3],[1,1,2],[0,1,2]])
B = A.T #转置矩阵
print('矩阵A的转置矩阵为：\n',B)

结果输出：

矩阵A的转置矩阵为：
 [[1 1 0]
 [2 1 1]
 [3 2 2]]

5.3 矩阵的逆

对于n阶矩阵A，如果存在一个n阶矩阵B，使得AB=BA=E，则称A为可逆矩阵，称B为A的逆矩阵，且逆矩阵是唯一的，记为B=A−1。

使用NumPy库中linalg模块的inv函数可以计算矩阵的逆，其语法格式如下：

numpy.linalg.inv(a)
# a:接收matrix，表示需要计算的矩阵。无默认值

求矩阵的逆矩阵：

import numpy as np#导入库Numpy
A = np.matrix([[1,2,3],[1,1,2],[0,1,2]])
B = np.matrix([[16,25],[20,8],[15,14]])
print('方法一：\n',(A.I)*B)
print('方法二：\n',np.linalg.inv(A)*B)

结果输出：

方法一：
 [[  5.  -6.]
 [-23.  20.]
 [ 19.  -3.]]
方法二：
 [[  5.  -6.]
 [-23.  20.]
 [ 19.  -3.]]

六、 协方差矩阵

设x=（x1，x2，…，xp）T和y=（y1，y2，…，yq）T分别为p维和q维随机向量，x和y的协方差矩阵（简称协方阵，记为cov（x，y）。

使用NumPy库中的cov函数可以求协方差矩阵，其语法格式如下：

numpy.cov(m,y=None,rowvar=Ture,bias=False,ddof=None,fweights=None,aweight=None)
# M:接收array或matrix，表示需要求协方差矩阵的数据。无默认值

设x为一个随机生成的2行5列的矩阵，求x的协方差矩阵。

import numpy as np#导入库Numpy
x = np.random.random(size=(2,5)) #生成2行5列的数据
Vx = np.cov(x)
print('矩阵x的协方差矩阵为：\n',Vx)

结果输出：

矩阵x的协方差矩阵为：
 [[ 0.07539891 -0.09921029]
 [-0.09921029  0.14076032]]

七、 相关矩阵

设x和y是两个随机变量，它们之间的相关系数定义为

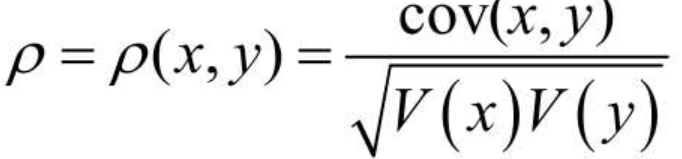
它度量了x和y之间线性相关关系的强弱，ρ的取值范围为［−1，1］。

当ρ=0时，表明x和y不相关；

当ρ>0时，表明x和y正相关；

当ρ<0时，表明x和y负相关；

当|ρ|=1时，当且仅当x和y中的一个变量可表示成另一个变量的线性函数。

使用NumPy库中的corrcoef函数可以求相关矩阵，其语法格式如下：

numpy.corrcoef(x,y=None,rowvar=Ture,bias=<class 'numpy._globals._NoValue'>,ddof=bias=<class 'numpy._globals._NoValue'>)
# x:接收array或matrix，表示需要求相关矩阵的数据。无默认值v

设x为一个随机生成的2行5列的矩阵，求x的相关矩阵。

import numpy as np#导入库Numpy
x = np.random.random(size=(2,5)) #生成2行5列的数据
P = np.corrcoef(x)
print('矩阵x的相关矩阵为：\n',P)

结果输出：

矩阵x的相关矩阵为：
 [[1.         0.10180246]
 [0.10180246 1.        ]]

八、 矩阵的特征值与特征向量

使用NumPy库中的linalg模块的eigvals函数可以计算一般矩阵的特征值，使用eig函数可以计算方阵的特征值和特征向量，其语法格式如下：

numpy.linalg.eigvals(a)
# x:接收array或matrix，表示需要求相关矩阵的数据。无默认值v
numpy.linalg.eig(a)
# x:接收array或matrix，表示需要求相关矩阵的数据。无默认值v

求矩阵A的特征值和特征向量。

import numpy as np#导入库Numpy
A = np.matrix([[3,-1],[-1,3]])
A1,A2 =np.linalg.eig(A)
A3 = np.linalg.eigvals(A)
print('方法一矩阵的特征值为：',A3)
print('方法二矩阵的特征值为：',A1)
print('方法二矩阵的特征向量为：\n',A2)

结果输出：

方法一矩阵的特征值为： [4. 2.]
方法二矩阵的特征值为： [4. 2.]
方法二矩阵的特征向量为：
 [[ 0.70710678  0.70710678]
 [-0.70710678  0.70710678]]
 #注：此处得到的特征向量是向量单位化之后的值，所以与前面的计算结果不完全一致。