动态规划之0-1背包问题
问题:
物品集合s={1,2,3,4,…,n},物品i的重量为wi,其价值为vi,背包的容量(最大载重量)为W,如何装使物品价值最大。(物品不能分割)
分析:
p(i,j)是背包容量为j,可选物品为i(i+1,…,n)时的最优解
(“将前i个物品放入容量为j的背包中”转化为只考虑物品i)
- p(i,j)=p(i+1,j)表示没装入第i个物品或者第i个物品的重量wi超过背包容量j。
- p(i,j)=p(i+1,j-wi)+vi表示装入物品i,价值增加vi,背包容量变为j-wi。
- 最后一个物品p(n,j),j大于wn,则能装入,价值增加vn,否则不能装入,价值增加0。
代码:
最优值:
#include<bits/stdc++.h>
using namespace std;
#define num 100//物品数量
#define num1 1000//背包容量
int w[num];//物品重量
int v[num];//物品价值
int p[num][num1];//递归数组
void value(int c,int n){//c表示背包容量W,n是物品数量
//边界
int jMax=min(w[n]-1,c);
//先将小的不可以装的置为0,将大于w[n]可以装的置为v[n]
for(int j=0;j<=jMAx;j++){
p[n][j]=0;
}
for(int j=w[n];j<=c;j++){
p[n][j]=v[n];
}
//计算递推式
for(int i=n-1;i>1;i--){
jMax=min(w[i]-1,c);
for(int j=0;j<=jMax;j++){
p[i][j]=p[i+1][j];
}
for(int j=w[i];j<=c;j++){
p[i][j]=max(p[i+1][j],p[i+1][j-w[i]+v[i]);
}
}
p[1][c]=p[2][c];
if(c>=w[1]){
p[1][c]=max(p[1][c],p[2][c-w[1]+v[1]);
}
}
最优解:
//用xi=0或1表示物品i装入或不装入背包
void jie(int c,int n,int x[]){
for(int i=1;i<n;i++){
if(p[i][c]==p[i+1][c]){
x[i]=0;
}
else{
x[i]=1;
c=c-w[i];
}
x[n]=(p[n][c])?1:0;
}
}
主函数:
int main(){
int x[num];
int W;
cin>>W;
int n;
cin>>n;
for(int i=1;i<=n;i++){
cin>>w[i]>>v[i];
}
memset(p,0,sizeof(p));
value(W,n);
cout<<p[1][W]<<endl;
jie(W,n,x);
for(int i=1;i<=n;i++){
if(x[i]){
cout<<i<<endl;
}
}
return 0;
}
测试:
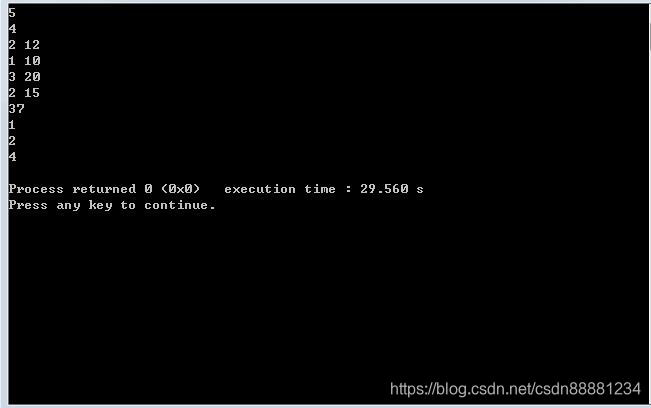







 本文详细解析了0-1背包问题的动态规划解决方案,通过递归数组p(i,j)来寻找在给定背包容量下,如何选择物品以达到最大价值。文章提供了完整的C++代码实现,并解释了如何通过比较p(i,j)和p(i+1,j)来确定每个物品是否被选中。
本文详细解析了0-1背包问题的动态规划解决方案,通过递归数组p(i,j)来寻找在给定背包容量下,如何选择物品以达到最大价值。文章提供了完整的C++代码实现,并解释了如何通过比较p(i,j)和p(i+1,j)来确定每个物品是否被选中。
















 760
760

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








