吴恩达机器学习（Machine Learning）课程总结笔记---Week4

0 概述

  前几周，我们对单变量，多变量以及逻辑回归进行了学习。对于简单的非线性回归，还可以使用多项式回归进行解决，但是对于更加复杂的问题，特征变量更多的问题，维数更多的问题，如果自行定义假设函数然后求解，则计算规模会遇到几何级数的增长困境。
  针对这样的情况，神经网络应运而生。

1. 课程大纲

本周课程大纲如下图所示：

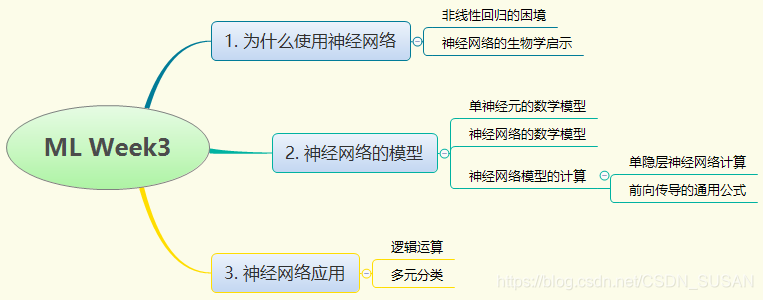
2. 课程内容

2.1 为什么要提出神经网络

2.1.1 非线性回归的困境

  现实世界往往是非线性的，前边我们讲到可以通过构造高级的特征项，用非线性的多项式回归进行拟合。
但是必须注意到，当特征量变位$n$，二阶特征项的规模为$\frac{n^2}{2}$，三阶特征项的规模为$O\left(n^3\right)$，随着特征量的规模变大，高阶项数呈几何级数上升。
  而对于大多数机器学习问题，$n$一般都比较大，因此需要提出一个新的方法来做非线性回归。

2.1.2 神经网络的生物学启示

  脑科学研究表明，大脑的视觉层可以学会听声音，舌头可以用来完成视觉功能，我们并没有给大脑创造一种新的方法，而只是简单的将视觉信号或者声音信号传递给到神经系统，神经系统就能够自动学会这些技能。
  因此，神经系统学家认为如果同一块脑组织可以处理光、声和触觉信号，那么就存在一种学习算法，可以同事处理视觉、听觉和触觉，而不需要为每一个信息处理编程，这就是神经网络提出的生物学启示。
生物学研究每一个神经元都可以被认为是一个神经核(处理单元)，包含很多输入(树突)和一个输出(轴突)，如下图所示，神经网络将会模仿此结构进行设计。

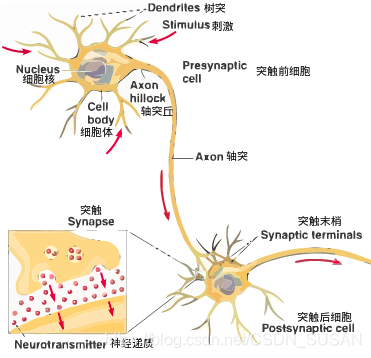
2.2 神经网络的模型表示

2.2.1 单个神经元的数学模型

上节中从生物学家角度上讲述了神经元的结构，模拟神经元，我们设计出如下图的数学模型：

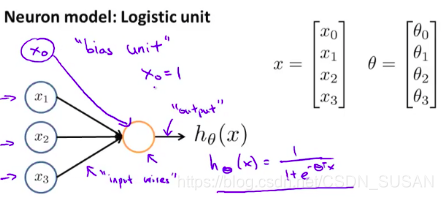
  $x_0$是手动加的偏置，$x_1,x_2,x_3$可以将其看成输入神经树突，黄色的圆圈则可以看成中心处理器细胞核， $h_{\theta }(x)$ 则可看成输出神经轴突。因为这里是逻辑单元，所以我们的输出函数为： $h_{\theta }(x)=\frac{1}{1+e^{-{\theta }^{T}x}}$ 。一般把它称为一个由s 型函数（逻辑函数）作为激励的人工神经元。

激励函数的作用是非线性化，还有其他几种常用的：
  阶跃函数，这是最简单直接的形式，也是人工神经网络定义时一般采用的。
  逻辑函数，就是S型函数（Sigmoid函数），具有可无限微分的优势。
  斜坡函数，RELU函数，最近比较火
  高斯函数

2.2.2 神经网络的数学模型

将单个神经元，组成完整的神经网络如下图所示：

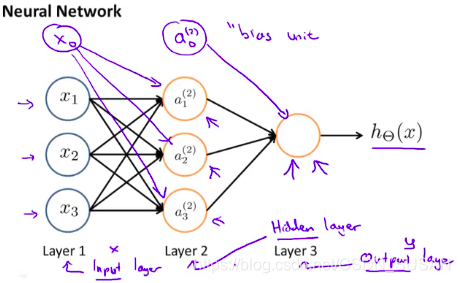
左边第一层 Layer1 被称为输入层。在输入层我们输入我们的特征项 $x_1,x_2,x_3$ 。
右边最后一层被称为输出层。输出函数为： $h_{\Theta }(x)$ 。
中间的所有层统称为隐藏层（还有多隐层的情况）。

2.2.3 神经网络模型的计算

如下图

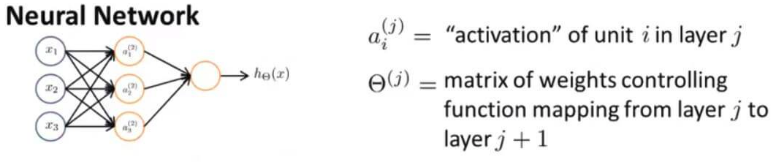
  其中隐藏层中的元素我们用 $a_i^{(j)}$ 表示。上标 j 表示的是第几层（有时候我们并不只有简单一层），下标 i 表示第几个。 $a_i^{(j)}$就是第j层的第i个节点（神经元）的“激活值”。
注意：这里$j$从2开始，因为输入层$\left[\begin{array}{l}{x}_0\\ x_1\\ x_2\\ x_3\end{array}\right]$，是第一层。

2.2.3.1 输入层到隐含层

$a_1^{(2)}=g\left({\Theta }_{10}^{(1)}{x}_0+{\Theta }_{11}^{(1)}{x}_1+{\Theta }_{12}^{(1)}{x}_2+{\Theta }_{13}^{(1)}{x}_3\right)$
$a_2^{(2)}=g\left({\Theta }_{20}^{(1)}{x}_0+{\Theta }_{21}^{(1)}{x}_1+{\Theta }_{22}^{(1)}{x}_2+{\Theta }_{23}^{(1)}{x}_3\right)$
$a_3^{(2)}=g\left({\Theta }_{30}^{(1)}{x}_0+{\Theta }_{31}^{(1)}{x}_1+{\Theta }_{32}^{(1)}{x}_2+{\Theta }_{33}^{(1)}{x}_3\right)$

其中，$x_0$为手动加入的偏置，通常为1；${\Theta }^{(j)}$表示第$j$层到第$j+1$层的权值矩阵；$g(x)$ 是 sigmoid 激活函数，即 $g(x)=\frac{1}{1+e^{-x}}$

2.2.3.2 隐含层到输出层

$h_{\Theta }(x)=a_1^{(3)}=g\left({\Theta }_{10}^{(2)}{a}_0^{(2)}+{\Theta }_{11}^{(2)}{a}_1^{(2)}+{\Theta }_{12}^{(2)}{a}_2^{(2)}+{\Theta }_{13}^{(2)}{a}_3^{(2)}\right)$
其中，$a_0^{(2)}$为隐含层的偏置，通常为1；输出层为第三层，因此$a_1^{(3)}$就等于$h_{\Theta }(x)$；$g(x)$ 是 sigmoid 激活函数，即 $g(x)=\frac{1}{1+e^{-x}}$

  由此可以得出，假如一个网络里面在第 j 层有 $s_j$ 个单元，在第 j+1 层有 $s_{j+1}$ 个单元，那么 ${\Theta }^{(j)}$ 则控制着第 j 层到第 j+1 层的映射矩阵，矩阵的维度是： $s_{j+1}\ast (s_j+1)$ 。

2.2.3.3 多隐层神经网络

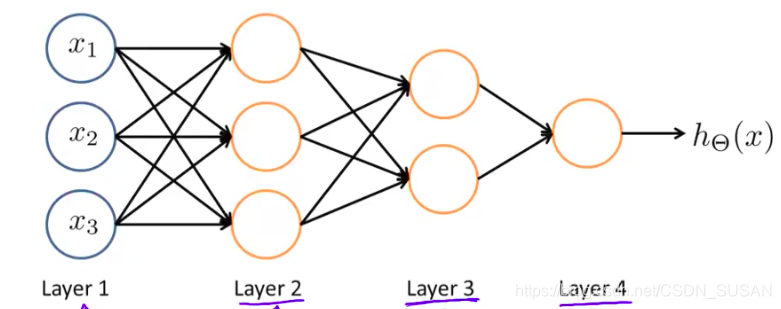
可以推导出，前向传播的通用公式，如下：
$\begin{array}{rl}{z}^{(j+1)}& ={\Theta }^{(j)}{a}^{(j)}\\ h_{\Theta }(x)& =a^{(j+1)}=g\left(z^{(j+1)}\right)\end{array}$
其中，当$j=1$时，上述公式就是一个逻辑回归神经元；当$j\in [1,2]$，则其表示单隐层神经网络的计算；依次类推
  神经网络正是这样解决比较复杂的函数，当层数很多的时候，我们有一个相对简单的输入量，通过加以权重和不同的运算送到第二层，而第三层在第二层作为输入的基础上再来进行一些更复杂的运算，每一层都可以看成是一种新的特征的构造，一层一层下去解决问题。

2.3 神经网络的应用

2.3.1 逻辑运算

以AND(与)为例，

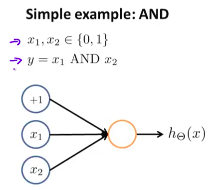
我们可以假设：M
$h_{\Theta }(x)=g\left({\Theta }_{10}^{(1)}{a}_0^{(1)}+{\Theta }_{11}^{(1)}{a}_1^{(1)}+{\Theta }_{12}^{(1)}{a}_2^{(1)}\right)=g(-30+20x_1+20x_2)$
通过真值表分析：

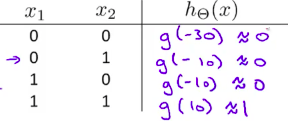
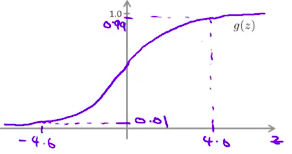
其中，S型函数的曲线图：

2.3.2 多元分类

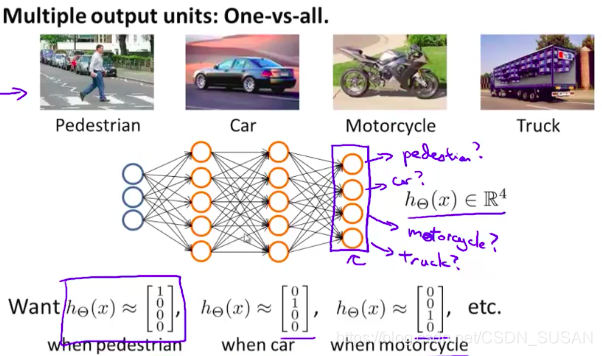
设计四个输出的神经网络即可。

3. 课后编程作业

我将课后编程作业的参考答案上传到了github上，包括了octave版本和python版本，大家可参考使用。
https://github.com/GH-SUSAN/Machine-Learning-MarkDown/tree/master/week4

4. 总结

本周通过探讨非线性回归的困境引入了神经网络，神经网络简单讲就是对大脑系统的模拟。
单个神经元，就是一个简单的逻辑回归(或者其他激活函数)，神经网络是多神经元的组合。
通过增加隐含层，对特征进行非线性化和升维处理从而得到新的构造特征，从而解决复杂的非线性回归问题。