【吴恩达系列】machine learning课程week4/5----神经网络

最新推荐文章于 2024-03-06 02:25:04 发布

菜鸡沈

最新推荐文章于 2024-03-06 02:25:04 发布

阅读量831

点赞数

分类专栏：吴恩达机器学习

本文链接：https://blog.csdn.net/weixin_42481299/article/details/106037642

版权

吴恩达机器学习专栏收录该内容

8 篇文章 0 订阅

订阅专栏

Week4：

- 神经网络

神经网络

1. 非线性回归的困境

在逻辑回归一章中，我们讨论了 0/1 分类问题，并且知道，通过对特征进行多项式展开，可以让逻辑回归支持非线性的分类问题。
假定我们现在有 $n$ 维特征，需要进行非线性分类，采用二次多项式扩展特征后，特征个数就为 $\frac{n^2}{2}$ 个特征，特征的空间复杂度就为 $O(n^2)$ ，如果扩展到三次多项式，则空间复杂度能达到 $O(n^3)$ ，随着特征量的规模变大，高阶项数呈几何级数上升。
而对于大多数机器学习问题， $n$ 一般都比较大，因此需要提出一个新的方法来做非线性回归。
下图中，房屋的特征由原来的 2 维增加到了 100 维，进行二次多项式扩展后，特征个数达到了约 5000 维（ $\frac{100\times 100}{2}$ ），对计算机的性能提出了很大的挑战。

2. 神经网络的模型表示

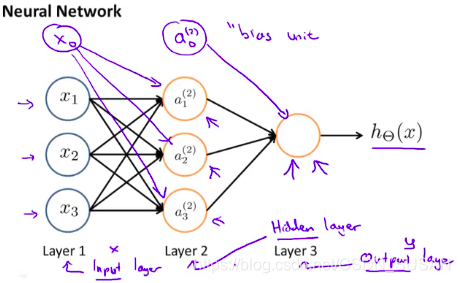
上图显示了人工神经网络是一个分层模型，逻辑上可以分为三层：

输入层：输入层接收特征向量 $x=[x1, x2, x3]^T$ 和一个偏置参数 $x_0$
输出层：输出层产出最终的预测 $h_\Theta(x)$
隐含层：隐含层介于输入层与输出层之间，之所以称之为隐含层，是因为当中产生的值并不像输入层使用的样本矩阵 $X$ 或者输出层用到的标签矩阵 $y$ 那样直接可见。

2.1 激励函数

2.1.1 第 $N$ 层以外层

隐含层在计算出 $z=-\Theta^T x$ 后，存在激活函数 $g(z)=\frac{1}{1+e^{-z}}$ 。

激励函数的作用是非线性化：

sigmoid： $g(z)=\frac{1}{1+e^{-z}} \in [0,1]$
tanh： $g(z)=\frac{e^{x}-e^{-x}}{e^{x}+e^{-x}} \in [-1,1]$
RELU： $\in [0,+\infin]$
softmax： $g(z)=\frac{e^{x_i}}{\sum_j^J e^{x_j}} \in [0,1]$

2.1.2 第 $N$ 层

在输出层：

回归(regression)： $g^{[N]}(x)=x$
二值化分类(binary classification)： $g^{[N]}(x)=sigmoid(x)$
多类分类(multiclass classification) ： $g^{[N]}(x)=softmax(x)$

对应损失函数：

实数值回归(regression)： $L(\hat{y},y)=\frac{1}{2}(\hat{y}-y)^2$
二值化分类(binary classification)： $L(\hat{y},y)=-y\log(\hat{y}) - (1-y)\log(1-\hat{y})$ 或负对数似然函数(negative log-likelihood)
$k$ 类分类(multiclass classification) ：交叉熵损失函数(cross entropy loss) $L(\hat{y},y)=-\sum^K_{j=1}1_{y=j}\log\hat{y}_j$

3. 前向传播和反向传播

3.1 前向传播过程（Forward Propagation）

$a^{(j)}_i$ 代表第 $j$ 层的第 $i$ 个激活单元。
$\Theta^{(j)}$ 代表从第 $j$ 层映射到第 $j + 1$ 层时的权重的矩阵。

其中，

$x_0$ ：手动加入的偏置，通常为1；
$\Theta(j)$ ：第 $j$ 层到第 $j + 1$ 层的权值矩阵；
$g (x)$ ：sigmoid 激活函数，即 $g(x)=\frac{1}{1+e−x}$

假如一个网络里面在第 $j$ 层有 $s_j$ 个单元，在第 $j + 1$ 层有 $s_{j+1}$ 个单元，那么 $\Theta(j)$ 则控制着第 $j$ 层到第 $j + 1$ 层的映射矩阵，矩阵的维度是： $s_{j+1}\times(s_j+1)$ 。

3.2 代价函数与L2正则化

$L$ ：神经网络总层数（包括输入层、隐层和输出层）
$s_l$ ：第L层的神经元数量（不包括手动加入的偏置 $a^{(l)}_0$
$K$ ：输出层的神经元数目

神经网络的层与层之间都可以看做构成了一个多个逻辑回归问题（根据神经元的数量），因此，其代价函数与逻辑回归的代价函数类似，其中 $K$ 代表类别， $l$ 表示层级，并且考虑了正规化：

逻辑回归的代价函数：
$J(\theta)=-\frac{1}{m}[\sum^n_{i=1} y^{(i)}\log(h_\theta(x^{(i)}) + (1-y^{(i)})\log(1-h_\theta(x^{(i)}))] + \frac{\lambda}{2m}\sum^n_{j=1}\theta^2_j$
神经网络的代价函数：
$J(\Theta)=-\frac{1}{m}[\sum^n_{i=1} \sum^K_{k=1} y^{(i)}_k\log((h_\Theta(x^{(i)}))_k) + (1-y^{(i)}_k)\log(1-(h_\Theta(x^{(i)})_k))] + \frac{\lambda}{2m}\sum^{L-1}_{l=1} \sum^{s_l}_{i=1}\sum^{s_l+1}_{j=1}(\Theta^{(l)}_{j,i})^2$

$h_\Theta(x)$ ：一个 $K$ 维向量，对应了训练集每个样本的输出向量 $y^{(i)}$
$i$ ：第 $i$ 个训练样本，总共有 $m$ 个
正则项：对系数矩阵 $\Theta$ 的每一个元素进行正则化（无偏置项系数）

⚠️补充：L2正则化 链接

两次求和只是将为输出层中的每个单元计算的逻辑回归成本相加
三次求和只是将整个网络中所有单独 $\Theta$ 的平方相加。
三次求和中的 $i$ 不代表训练示例 $i$

其矩阵表示为：
$J(\Theta)=-\frac{1}{m}\sum(Y^T.*\log(\Theta A)+(1−Y^T).*\log(1−\Theta A))$ 其中，
$A\in R^{(K\times m)}$ ：所有样本对应的输出矩阵，其每一列对应一个样本的输出，
$Y\in R^{(m\times K)}$ ：标签矩阵，其每行对应一个样本的类型。

3.3 反向传播过程（Back Propagation）

与回归问题一样，我们也需要通过最小化代价函数 $J(\Theta)$ 来优化预测精度的，但是，由于神经网络允许多个隐含层，即，各层的神经元都会产出预测，因此，就不能直接利用传统回归问题的梯度下降法来最小化 $J(\Theta)$ ，而需要逐层考虑预测误差，并且逐层优化。
为此，在多层神经网络中，使用反向传播算法（Backpropagation Algorithm）来优化预测，首先定义各层的预测误差为向量 $\delta(l)$ ：

$\delta^{(l)} = \left\{ \begin{array}{rcl} a^{(l)}−y & & {l=L}\\ (\Theta^{(l)})^T\delta^{(l+1)}).∗g'(z^{(l)}) & & {l=2,3,\dots,L-1}\\ \end{array} \right.$
其中： $g'(z^{(l)})=a^{(l)}.∗(1−a^{(l)})$
反向传播中的反向二字也正是从该公式中得来，本层的误差 $\delta^{(l)}$ 需要由下一层的误差 $\delta^{(l+1)}$ 反向推导。
注意： $\delta^{(1)}$ 不用求解，因为输入和实际的没有偏差。

⚠️补充：计算过程和优化 链接

3.4 神经网络的训练过程

假定有训练集 $(x^{(1)}, y^{(1)}),\dots,(x^{(m)},y^{(m)})$ ，使用了反向传播的神经网络训练过程如下：

for all $l, i, j$ ，初始化权值梯度 $\Delta^{(l)}$ : $\Delta^{(l)}_{i,j}=0$
for $i = 1$ to $m$ :
                       $a^{(1)}=x^{i}$
                       执行前向传播算法，计算各层的激活向量： $a^{(l)}$
                       通过标签向量 $y^{(i)}$ ，计算输出层的误差向量： $\delta^{(L)}=a^{(L)}−y^{(i)}$
                       反向依次计算其他层误差向量： $\delta^{(L−1)},\delta^{(L−2)},\dots,\delta^{(2)}$
                       求 $\Delta^{(l)}_{ij}:=\Delta^{(l)}_{ij}+a^{(l)}_j \delta^{(l+1)}_i$ ，即： $\Delta^{(l)}:=\Delta^{(l)}_{ij}+\delta^{(l+1)}(a^{(l)})^T$
求各层权值的更新增量 $D^{(l)}$ ，连接偏置的权值不进行正规化：
$D^{(l)}_{ij} = \left\{ \begin{array}{rcl} \frac{1}{m}\Delta^{(l)}_{ij} + \lambda \Theta^{(l)}_{ij} & & {if j \neq 0}\\ \frac{1}{m}\Delta^{(l)}_{ij} & & {if j = 0}\\ \end{array} \right.$
更新各层的权值矩阵 $\Theta^{(l)}$ ，其中 $\alpha$ 为学习率： $\Theta^{(l)}=\Theta^{(l)}-\alpha D^{(l)}$

3.5 编程算法实现

3.5.1 参数展开（Unrolling Parameters）

为了利用梯度下降的优化算法，需要用到 fminunc 函数。其输入的参数 $\Theta$ 必须是向量，函数的返回值是代价函数 jVal 和导数值 gradient。
所以将参数矩阵展开成一个 $n * 1$ 的向量，方便参数的传递。
具体操作：假如 $\Theta_1$ , $\Theta_2$ , $\Theta_3$ 参数和 $D^{(1)}$ , $D^{(2)}$ , $D^{(3)}$ 参数， $\Theta_1$ 是 $10 * 11$ 维， $\Theta_2$ 是 $10 * 11$ 维， $\Theta_3$ 是 $1 * 11$ 维。

% matlab：
% 打包成一个向量
thetaVector = [ Theta1(:); Theta2(:); Theta3(:); ]
deltaVector = [ D1(:); D2(:); D3(:) ]

% 解包还原
Theta1 = reshape(thetaVector(1:110),10,11)
Theta2 = reshape(thetaVector(111:220),10,11)
Theta3 = reshape(thetaVector(221:231),1,11)

链接

3.5.2 梯度校验（Gradient Checking）

理论上，在我们使用梯度下降的时候， $J(\Theta)$ 每次都会下降。但是由于反向传播的复杂性，可能导致计算过程存在bug，因此需要进行梯度检验，以减少错误的概率。
使用双侧差分算法，近似求解偏导数。

斜边的斜率可以近似等于蓝色线段的斜率，亦即，可以通过求取红色斜边的斜率来近似 $\frac{d}{d\Theta}J(\Theta)$
$\frac{d}{d\Theta}J(\Theta) \approx \frac{J(\Theta+\epsilon) - J(\Theta-\epsilon)}{2\epsilon}$

通常， $\epsilon$ 取较小值，如 0.01

总结一下：

通过反向传播来计算偏导数DVec
使用双侧差分计算近似偏导
比较Dvec是否约等于近似偏导

使用算法学习的时候记得要关闭这个梯度检验，梯度检验只在代码测试阶段进行。

3.5.3 权值初始化

0 值初始化：
在逻辑回归中，我们通常会初始化所有权值为0 ，假如在如下的神经网络也采用 0 值初始化：

如图所示，如果初始化位全0矩阵，则进行反向传播计算偏导时，对于所有 $\Theta^{(l)}_{ij}$ 的偏导是一样的。这就导致了在参数更新的情况下，两个参数是一样的。无论怎么重复计算其两边的激励还是一样的。
上述问题被称为对称权重问题，也就是所有权重都是一样的。所以随机初始化是解决这个问题的方法。
随机初始化
将初始化权值 $\Theta^{(l)}_{ij}$ 的范围限定在 $[−\epsilon, \epsilon]$ ，产生随机数，初始化权值矩阵。

% matlab：
% If the dimensions of Theta1 is 10x11, Theta2 is 10x11 and Theta3 is 1x11.
Theta1 = rand(10,11) * (2 * INIT_PHI) - INIT_PHI;
Theta2 = rand(10,11) * (2 * INIT_PHI) - INIT_PHI;
Theta3 = rand(1,11) * (2 * INIT_PHI) - INIT_PHI;

Xavier/He 初始化
对权重(weights)进行的初始化如下：
$w^{[l]} \sim \mathcal{N}(0,\sqrt{ \frac{2}{n^{[l]}+n^{[l-1]}}})$
上式中的 $n^{[l]}$ 表示的是第 $l$ 层的神经元个数。

这种操作是一种最小规范化技术(mini-normalization technique)。
对于单层而言，设该层的输入(input)的方差(variance)是 $\sigma^{(in)}$ ，而输出(也就是激活状态函数，activations)的方差是 $\sigma^{(out)}$ 。
Xavier/He 初始化就是让 $\sigma^{(in)}$ 尽量接近 $\sigma^{(out)}$ 。

3.6 前向传播的应用

3.6.1 逻辑运算

AND: $\Theta^{(1)}=\begin{bmatrix}−30 & 20 & 20\end{bmatrix}$
NOR: $\Theta^{(1)}=\begin{bmatrix}10 &−20 &−20\end{bmatrix}$
OR: $\Theta^{(1)}=\begin{bmatrix}−10 &20 &20\end{bmatrix}$

3.6.1 多元分类

4. 神经网络使用步骤总结

STEP 1：设计神经网络

输入单元个数，是输入变量的 $x^{(i)}$ 的维度（特征数量）
输出单元是分类结果的个数
隐层的单元数，理论上越多越好，但是考虑计算成本均衡问题。默认1个隐层，如果有多隐层，则建议每个隐层单元数相同。

STEP 2 ：训练神经网络

随机初始化权重。初始化的值是随机的，值很小，接近于零。
执行前向传播算法，对于每一个样本 $x^{(i)}$ 计算出假设函数 $h_\Theta(x^{(i)})$ 计算出代价函数 $J(\Theta)$
执行反向传播算法，计算出偏导数 $\frac{\partial}{\partial \Theta^{(l)}_{jk}}J(\Theta)$
利用梯度检查，对比反向传播算法计算得到的偏导数项是否与梯度检验算法计算出的导数项基本相等。
我们利用梯度下降算法或者更高级的算法例如 LBFGS、共轭梯度法等，结合之前算出的偏导数项，最小化代价函数 $J(\Theta)$ 算出权值的大小 $\Theta$

理想状态下，满足 $h_\Theta(x^{(i)}) \approx y^{(i)}$ ，就认为代价函数最小了，由于代价函数 $J(\Theta)$ 是非凸的，因此我们最终可以用局部最小值代替全局最小值。

Python代码：

http://cs229.stanford.edu/notes/backprop.py
import numpy as np
from copy import copy

# Example backpropagation code for binary classification with 2-layer
# neural network (single hidden layer)

sigmoid = lambda x: 1 / (1 + np.exp(-x))

def fprop(x, y, params):
  # Follows procedure given in notes
  W1, b1, W2, b2 = [params[key] for key in ('W1', 'b1', 'W2', 'b2')]
  z1 = np.dot(W1, x) + b1
  a1 = sigmoid(z1)
  z2 = np.dot(W2, a1) + b2
  a2 = sigmoid(z2)
  loss = -(y * np.log(a2) + (1-y) * np.log(1-a2))
  ret = {'x': x, 'y': y, 'z1': z1, 'a1': a1, 'z2': z2, 'a2': a2, 'loss': loss}
  for key in params:
    ret[key] = params[key]
  return ret

def bprop(fprop_cache):
  # Follows procedure given in notes
  x, y, z1, a1, z2, a2, loss = [fprop_cache[key] for key in ('x', 'y', 'z1', 'a1', 'z2', 'a2', 'loss')]
  dz2 = (a2 - y)
  dW2 = np.dot(dz2, a1.T)
  db2 = dz2
  dz1 = np.dot(fprop_cache['W2'].T, dz2) * sigmoid(z1) * (1-sigmoid(z1))
  dW1 = np.dot(dz1, x.T)
  db1 = dz1
  return {'b1': db1, 'W1': dW1, 'b2': db2, 'W2': dW2}

# Gradient checking

if __name__ == '__main__':
  # Initialize random parameters and inputs
  W1 = np.random.rand(2,2)
  b1 = np.random.rand(2, 1)
  W2 = np.random.rand(1, 2)
  b2 = np.random.rand(1, 1)
  params = {'W1': W1, 'b1': b1, 'W2': W2, 'b2': b2}
  x = np.random.rand(2, 1)
  y = np.random.randint(0, 2)  # Returns 0/1

  fprop_cache = fprop(x, y, params)
  bprop_cache = bprop(fprop_cache)

  # Numerical gradient checking
  # Note how slow this is! Thus we want to use the backpropagation algorithm instead.
  eps = 1e-6
  ng_cache = {}
  # For every single parameter (W, b)
  for key in params:
    param = params[key]
    # This will be our numerical gradient
    ng = np.zeros(param.shape)
    for j in range(ng.shape[0]):
      for k in xrange(ng.shape[1]):
        # For every element of parameter matrix, compute gradient of loss wrt
        # that element numerically using finite differences
        add_eps = np.copy(param)
        min_eps = np.copy(param)
        add_eps[j, k] += eps
        min_eps[j, k] -= eps
        add_params = copy(params)
        min_params = copy(params)
        add_params[key] = add_eps
        min_params[key] = min_eps
        ng[j, k] = (fprop(x, y, add_params)['loss'] - fprop(x, y, min_params)['loss']) / (2 * eps)
    ng_cache[key] = ng

  # Compare numerical gradients to those computed using backpropagation algorithm
  for key in params:
    print key
    # These should be the same
    print(bprop_cache[key])
    print(ng_cache[key])