最小生成树 kruskal_使用Kruskal算法求解Java最小生成树问题

最小生成树 kruskal

In Electronic Circuit we often required less wiring to connect pins together. We can model this wiring problem with a connected, undirected graph G=(V, E), where V is the set of pins, E is the set of possible interconnections between pair of pins, and for each edge we have a weight w(u,v) specifying the cost (amount of wire needed) to connect u and v. We then wish to find an acyclic subset T that connects all of the vertices and whose total weight w(T)= sum of all the weights in T is minimized . Since T is acyclic and connects all of the vertices, it must form a tree, which we call a spanning tree since it spans the graph G. We call this problem minimum spanning tree problem.

在电子电路中，我们通常需要较少的接线来将引脚连接在一起。 我们可以使用连接的无向图G =(V，E)来建模此布线问题，其中V是引脚组， E是引脚对之间可能的互连集，对于每个边，我们都有权重w( u，v)指定连接u和v的成本(所需的电线数量)。 然后，我们希望找到一个无环子集T ，它连接所有顶点，并且总权重w(T)= T中所有权重的总和最小 。 由于T是无环的并且连接所有顶点，因此它必须形成一棵树，由于它跨越了图G ，因此我们将其称为生成树 。 我们称这个问题为最小生成树问题 。

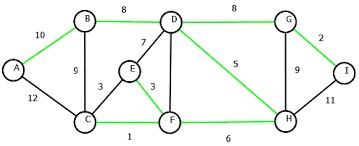
MST Green color edges are the selected edges for MST.

MST绿色边缘是MST的选定边缘。

There are two algorithm to solve this problem: Kruskal's Algorithm and Prim's Algorithm. Each of them run in O(E lg V )

有两种算法可以解决此问题： Kruskal算法和Prim算法 。 它们每个都以O(E lg V)运行

Here we are discussing Kruskal's Algorithm...

在这里，我们讨论的是Kruskal算法...

克鲁斯卡尔算法 (Kruskal's Algorithm)

This Algorithm first makes the forest of each vertex and then sorts the edges according to their weights, and in each step, it adds the minimum weight edge in the tree that connects two distinct vertexes that do not belong to the same tree in the forest.

该算法首先创建每个顶点的森林，然后根据其权重对边缘进行排序，然后在每个步骤中，在连接两个不属于该森林中同一棵树的不同顶点的树中添加最小权重边缘。

It uses a disjoint set data structure to maintain several disjoint sets of elements. Each set contains the vertices in one tree of the current forest.

它使用不连续集数据结构来维护几个不连续元素集。 每一组包含当前森林的一棵树中的顶点。

Example: Here we are finding the cost of MST.

示例：在这里我们发现MST的成本。

Program:

程序：

import java.io.*;
import java.util.*;
import java.text.*;
import java.math.*;
import java.util.regex.*;

public class MST{
	
	static class set{
		int parent,rank;
	}
	
	//find set which represents vertex i
	static int find(set subsets[],int i ){
		if(subsets[i].parent==i)
			return i;
		return find(subsets,subsets[i].parent);
	}
	
	//function for adding  edges whose vertex belongs 
	//to the different tree ie. UNION
	static void UNION(set subsets[],int x,int y){
		int xroot=find(subsets,x);
		int yroot=find(subsets,y);

		if(subsets[xroot].rank>subsets[yroot].rank)
			subsets[yroot].parent=xroot;
		else if(subsets[xroot].rank<subsets[yroot].rank)
			subsets[xroot].parent=yroot;
		else{
			subsets[yroot].parent=xroot;
			subsets[xroot].rank++;
		}
	}
	
	static int mst(int n, Integer[][] edges) {
		set subsets[]=new set[n];

		//Create forest of vrtices that is separate tree for each vertex
		for(int i=0;i<n;i++)   
		{  
			subsets[i]=new set();
			subsets[i].parent=i;  // Each vertex is its own parent
			subsets[i].rank=0;   //Having no child
		}

		int e=0,i=0,count=0;
		//Create graph having exactly vertex-1 ie. n-1 edges
		while(e<n-1){
			//find set from which current vertex belongs
			int x=find(subsets,edges[i][0]-1);  
			//find set from which current vertex belongs
			int y=find(subsets,edges[i][1]-1); 

			if(x!=y){
				count+=edges[i][2];  
				e++;
				// union the two vertex in the same tree 
				//if they belong to the different set
				UNION(subsets,x,y); 
			}
			i++;
		}
		return count;
	}

	public static void main(String[] args) 
	{
		Scanner in = new Scanner(System.in);
		int n = in.nextInt();   //number of nodes
		int m = in.nextInt();  //number of edges
		Integer [][]edges = new Integer[m][3];
		for(int edges_i = 0; edges_i < m; edges_i++){
			for(int edges_j = 0; edges_j < 3; edges_j++){
				edges[edges_i][edges_j] = in.nextInt();
			}
		}
		
		//Sort edges two dimensional array according to 
		//its third column i.e. weight
		Arrays.sort(edges,new Comparator<Integer[]>(){
			@Override
			public int compare(Integer[] i1,Integer[] i2){
				//Comparing third column having index 2
				return i1[2].compareTo(i2[2]);   
			}
		});
		
		int result=mst(n,edges);
		System.out.println(result);
		in.close();
	}
}

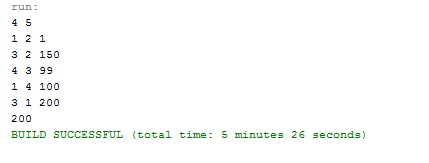
Output

输出量

翻译自: https://www.includehelp.com/java/minimum-spanning-tree-problem-using-kruskals-algorithm.aspx

最小生成树 kruskal