8x8矩阵显示数字程序_在矩阵中填写8个数字

8x8矩阵显示数字程序

Description:

描述：

This is a standard interview problem to fill a matrix with 8 numbers using backtracking.

这是一个标准的面试问题，即使用回溯来用8个数字填充矩阵。

Problem statement:

问题陈述：

A matrix is given to you and eight vacant spaces are there. You have to fill the places with the digits 1 to 8 in a way that there are not any adjacent places filled with its next digits.

将为您提供一个矩阵，那里有八个空位。 您必须以1到8的数字来填充地点，以确保相邻的地方都不会填充其下一个数字。

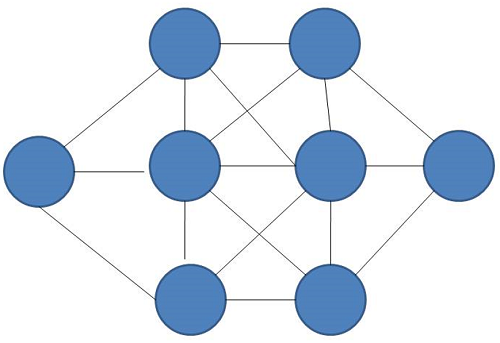
    Input:
    An matrix given to you
    
    E.g.
    0 -1 -1 0
    -1 -1 -1 -1
    0 -1 -1 0
    
    Here -1 indicates the vacant places in the matrix.
    
    Output:
    Print the matrix with the numbers.

Example

例

    If the matrix is this:
    0 -1 -1 0
    -1 -1 -1 -1
    0 -1 -1 0

    Output:
    0 3 5 0
    7 1 8 2
    0 4 6 0

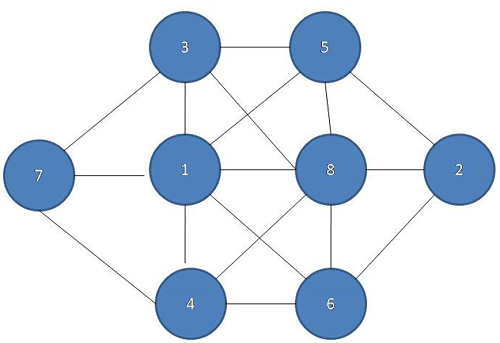
Explanation with example

举例说明

Placing the proper numbers in the right place is a try and error process and to solve it we use the backtracking process. To solve the matrix we have to follow the following steps.

将正确的数字放置在正确的位置是一个反复尝试的过程，为了解决这个问题，我们使用了回溯过程。 要求解矩阵，我们必须遵循以下步骤。

1. Start with a vacant place.

   从一个空旷的地方开始。

2. Check how many numbers are left to fit for the place.

   检查剩余多少个数字以适合该位置。

3. Start with any of the remaining numbers and check that its next numbers are not in its adjacent places.

   从其余任何数字开始，然后检查其下一个数字是否不在其相邻位置。

4. Place the proper number in that vacant place and go for the adjacent vacant place.

   将适当的编号放在该空位，然后移至相邻的空位。

If the matrix is this,

如果矩阵是这个

And we start with the vacant place (1,2) and put the number 1 and if we will go (1,3), (2,3), (2,2), (2,4), (2,1) points followed by (1,2) and putting the numbers 3, 7, 2, 5. Then there are two vacant places but we will not fill those places with the numbers 8 or 6.

然后从空位(1,2)开始 ，然后将数字1放到(1,3)，(2,3)，(2,2)，(2,4)，(2,1 )点，随后(1,2)，并把数字3,7，2,5。 然后有两个空位，但我们不会用数字8或6填充这些空位。

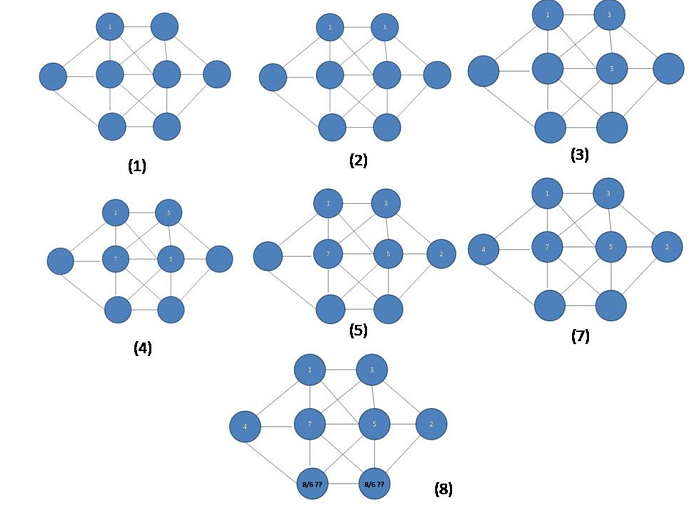
So using the backtracking method, in the place of (2,3) will put the next number 6 and again applying the same method to fill all the vacant places with the numbers.

因此，使用回溯方法，将(2,3)放在下一个数字6处，然后再次应用相同的方法用数字填充所有空缺位置。

C++ implementation:

C ++实现：

#include <bits/stdc++.h>
using namespace std;

int x[8] = { 0, 0, 1, -1, 1, -1, -1, 1 };
int y[8] = { -1, 1, 0, 0, -1, -1, 1, 1 };

//check the validity of the point
bool is_valid(int row, int col, int a, int b)
{
    return (a >= 0 && a < row && b >= 0 && b < col);
}

bool all_visited(int* mat, int row, int col)
{
    int count = 0;

    for (int i = 0; i < row; i++) {
        for (int j = 0; j < col; j++) {
            if (*(mat + i * col + j) == -1) {
                return false;
            }
        }
    }
    return true;
}

bool print_matrix(int* mat, int row, int col)
{
    for (int i = 0; i < row; i++) {
        for (int j = 0; j < col; j++) {
            cout << *(mat + i * col + j) << " ";
        }
        cout << endl;
    }
    return true;
}

bool is_safe(int* mat, int row, int col, int curr_row, int curr_col, int curr)
{
    for (int j = 0; j < 8; j++) {
        int x_axis = curr_row + x[j];
        int y_axis = curr_col + y[j];

        //checking for the next numbers
        if (is_valid(row, col, x_axis, y_axis) && *(mat + x_axis * col + y_axis) != -1 && *(mat + x_axis * col + y_axis) != 0 && ((curr > 1 && (*(mat + x_axis * col + y_axis) == curr - 1 || *(mat + x_axis * col + y_axis) == curr + 1)) || (curr == 1 && *(mat + x_axis * col + y_axis) == curr + 1))) {
            return false;
        }
    }
    return true;
}

bool fill_matrix(int* mat, int row, int col, int curr_row, int curr_col, bool* visited, int prev)
{
    int flag = 0;

    for (int i = 1; i <= 8; i++) {
        //if the point is not visited
        if (!visited[i] && is_safe(mat, row, col, curr_row, curr_col, i)) {
            visited[i] = true;
            *(mat + curr_row * col + curr_col) = i;
            if (all_visited(mat, row, col))
                return true;
            for (int j = 0; j < 8; j++) {
                //go for the adjacents points
                int x_axis = curr_row + x[j];
                int y_axis = curr_col + y[j];
                if (is_valid(row, col, x_axis, y_axis) && *(mat + x_axis * col + y_axis) == -1 && fill_matrix(mat, row, col, x_axis, y_axis, visited, i)) {
                    return true;
                }
            }
            visited[i] = false;
            *(mat + curr_row * col + curr_col) = -1;
        }
    }
    return false;
}

int main()
{
    int mat[3][4] = { { 0, -1, -1, 0 },
        { -1, -1, -1, -1 },
        { 0, -1, -1, 0 } };

    int flag = 0, prev = -1;
    bool visited[9];

    for (int i = 0; i < 9; i++) {
        visited[i] = false;
    }

    for (int i = 0; i < 3; i++) {
        for (int j = 0; j < 4; j++) {
            if (mat[i][j] == -1) {
                fill_matrix(&mat[0][0], 3, 4, i, j, visited, prev);
                flag = 1;
                break;
            }
        }
        if (flag)
            break;
    }

    //print the matrix
    print_matrix(&mat[0][0], 3, 4);
    return 0;
}

Output

输出量

0 6 4 0
2 8 1 7
0 5 3 0

翻译自: https://www.includehelp.com/icp/fill-8-numbers-in-a-matrix.aspx

8x8矩阵显示数字程序