C ++和C＃程序员浮点格式简要指南

最新推荐文章于 2023-06-06 20:27:05 发布

cunhan4654

最新推荐文章于 2023-06-06 20:27:05 发布

阅读量711

点赞数

文章标签： c++ java python stream 编程语言

原文链接：https://www.codeproject.com/Articles/5255408/Succinct-Guide-to-Floating-Point-Format-For-Cplusp

版权

Floating-Point Dissector is available for download at GitHub.

浮点分解器可从GitHub下载。

目录 (Table of Contents)

介绍 (Introduction)

The IEEE 754 standard for floating-point format has been ubiquitous in hardware and software since established in 1985. Programmers has been using floating-point indiscriminately for real-number calculations. However, not many can claim to understand floating-point format and its properties, so more than a few misunderstandings has arisen. In this new year and new decade, I throw down the gauntlet as a challenge to myself to write a concise and easy-to-digest guide to explain floating-point once and for all. Common pitfalls shall be covered.

自1985年建立以来，用于浮点格式的IEEE 754标准在硬件和软件中已无处不在。程序员一直不加选择地使用浮点进行实数计算。但是，没有多少人可以声称了解浮点格式及其属性，因此产生了许多误解。在这个新的新年和新的十年中，我放弃了挑战，这是对我自己的挑战，因为他写了一个简明易懂的指南来一劳永逸地解释浮点。应当注意常见的陷阱。

浮点分解器 (Floating-Point Dissector)

Floating-Point Dissector (with C++ and C# version) is written for programmers to examine floating-point bits after setting its value. Only class to check single(32-bit) and double(64-bit) precision are written for. Main reason is half(16-bit), long double(80-bit) and quad(128-bit) precision are not directly supported on Microsoft platform. Code for single and double precision dissector are identical, their only difference are the constants defined at the top of each class. C++ experts should see this code ripe for template and type traits. But I prefer to keep things simple as there are only 2 class for single and double. See the usage of C# code below on how to view the single precision of value 1 with the Display() method. C++ code is not shown because it is similar.

编写浮点分解器(具有C ++和C＃版本)供程序员在设置其值之后检查浮点位。仅编写用于检查单(32位)和双(64位)精度的类。主要原因是Microsoft平台不直接支持一半(16位)，长双精度(80位)和四精度(128位)精度。单精度和双精度解剖器的代码相同，唯一的区别是在每个类的顶部定义的常数。 C ++专家应该看到针对模板和类型特征的此代码已成熟。但我还是想保持简单，因为单人和双人间只有2个班级。有关如何使用Display()方法Display()值1的单精度的信息，请参见下面的C＃代码用法。由于类似，所以未显示C ++代码。

FloatDissector f = new FloatDissector(1.0f);
f.Display();

The output from Display() is shown below. Adjusted Exponent is the true value. Adjusted Exponent = Raw Exponent - Exponent Bias. Exponent Bias in single precision case is 127. More on this later when we get to the floating-point format section.

Display()的输出如下所示。调整后的指数是真实值。 Adjusted Exponent = Raw Exponent - Exponent Bias 。单精度情况下的指数偏差为127 。稍后我们将在浮点格式部分中详细介绍。

Sign:Positive, Adjusted Exponent:0, Raw Exponent:01111111, Mantissa:00000000000000000000000, Float Point Value:1

There are also methods to set Not-a-Number(NaN), Infinity(INF). There are 2 ways to set a NaN. The first way is to pluck the NaN from double type and give it to constructor. The second way is the DoubleDissector.SetNaN() method whose first parameter is the sign bit and the second one is mantissa which can be any value but shall be greater than zero beause a zero mantissa does not constitute a NaN. This indirectly implied there are more than 1 NaN value.

也有设置Not-a-Number( NaN )，Infinity(INF)的方法。有两种设置NaN 。第一种方法是从double类型中提取NaN并将其提供给构造函数。第二种方法是DoubleDissector.SetNaN()方法，其第一个参数是符号位，第二个方法是尾数，尾数可以是任意值，但应大于零，因为零尾数不构成NaN 。这间接暗示存在大于1的NaN值。

DoubleDissector d = new DoubleDissector(double.NaN); // set NaN

d.SetNaN(DoubleDissector.Sign.Positive, 2); // NaN can be set this way as well.

Console.WriteLine("IsNaN:{0}", d.IsNaN());
Console.WriteLine("IsZero:{0}", d.IsZero());
Console.WriteLine("IsInfinity:{0}", d.IsInfinity());
Console.WriteLine("IsPositiveInfinity:{0}", d.IsPositiveInfinity());
Console.WriteLine("IsNegativeInfinity:{0}", d.IsNegativeInfinity());
Console.WriteLine("IsNaN:{0}", double.IsNaN(d.GetFloatPoint()));

After the end of the guide, reader shall be confident of implementing his own dissector.

指南结束后，读者应有信心实施自己的解剖器。

常见的误解 (Common Misconceptions)

It is a common knowledge among programmers that floating-point format is unable to represent transcendental numbers like PI and E whose fractional part continues on indefinitely. It is not unusual to see a very high precision PI literal is defined in C/C++ code snippets whose the original poster take a leap of faith that the compiler try its best possible effort to quantize into IEEE 754 format and do rounding when needed. Taking 32-bit float as an example, the intention goes as planned (See diagram below).

程序员之间的常识是，浮点格式无法表示先验数字，例如PI和E，其小数部分会无限期地继续。在C / C ++代码片段中定义了非常高精度的PI文字并不罕见，其原始海报让人相信编译器会尽最大努力量化为IEEE 754格式并在需要时进行舍入。以32位浮点数为例，该意图按计划进行(请参见下图)。

Surprise pop up for E. As it turns out, there are finite bits in a floating-point to perform quantization from a floating-point literal. Reality sets in when a simple number like 0.1 cannot be represented in single precision perfectly as well.

事实证明，E会弹出惊喜。事实证明，浮点数中有有限的位可以根据浮点文字进行量化。当不能像单精度那样完美地表示0.1类的简单数字时，现实就会出现。

float a = 0.1f;
Console.WriteLine("a: {0:G9}", a);

Output is as follows.

输出如下。

a: 0.100000001

数学身份(关联，交换和分配)不成立。 (Mathematical identities (associative, commutative and distributive) do not hold.)

Associative rule does not apply.

关联规则不适用。

x + (y + z) != (x + y) + z

Commutative rule does not apply.

交换规则不适用。

x * y != y * x

Distributive rule does not apply.

分配规则不适用。

x * y - x * z != x(y - z)

In fact with floating-point arithmetic, the order of computation matters and the result can change on every run when order changes. Programmer can be tripped by this if he rely on your result to be consistent. During C++17 standardization, the parallelized version of std::accumulate() was given a new name: std::reduce() so as to let people know this parallelized function can return different result.

实际上，对于浮点运算，计算顺序很重要，并且每次更改顺序时，结果都会在每次运行中更改。如果程序员依靠您的结果是一致的，那么程序员可能会因此而感到困惑。在C ++ 17标准化期间， std :: accumulate()的并行化版本被赋予了新名称： std :: reduce() ，以使人们知道此并行化函数可以返回不同的结果。

Division and multiplication cannot be interchanged. Common misconception claimed division is more accurate than multiplication. This is not true. These 2 operations could yield slighly different results.

除法和乘法不能互换。常见的误解声称除法比乘法更准确。这不是真的。这两个操作可能会产生截然不同的结果。

x / 10.0 != x * 0.1

浮点数转换为整数 (Floating-Point Conversion to Integer)

Floating-point conversion to integer can be done with a int cast. The caveat is the cast actually truncate it towards zero which may not be desired.

浮点数到整数的转换可以通过int cast进行。注意事项是强制转换实际上将其截断为零，这可能是不希望的。

float f = 2.9998f;
int num = (int)(f); // num is 2

To fix this problem, add 0.5 before casting.

要解决此问题，请在投射前添加0.5 。

float f = 2.9998f;
int num = (int)(f + 0.5f); // num is 3 now

To cater for negative value,

为了应对负值，

if(f < 0.0f)
    num = (int)(f - 0.5f);
else
    num = (int)(f + 0.5f);

A better solution for C# is to use the static Math.Round method.

C＃的更好解决方案是使用静态Math.Round方法。

int a = (int)Math.Round(4.5555);      // a == 5

Math.Round is very convenient to use. But it has to be noted that rounding follows IEEE Standard 754, section 4 standard. This means that if the number being rounded is halfway between two numbers, the Round operation shall always round to the even number.

Math.Round使用Math.Round非常方便。但是必须注意，四舍五入遵循IEEE标准754，第4节标准。这意味着，如果四舍五入的数字是两个数字之间的一半，则“ Round运算应始终四舍五入为偶数。

int x = (int)Math.Round(1.5);      // x == 2
int y = (int)Math.Round(2.5);      // y == 2

For C++ 11, std::round and std::rint are available for rounding. std::rint operates according to the rounding rules set by calls to std::fesetround. If the current rounding mode is...

对于C ++ 11，可使用std :: round和std :: rint进行舍入。 std::rint根据对std :: fesetround的调用设置的舍入规则进行操作。如果当前的舍入模式为...

FE_DOWNWARD, then std::rint is equivalent to std::floor.
FE_DOWNWARD ，则std::rint等同于std::floor 。
FE_UPWARD, then std::rint is equivalent to std::ceil.
FE_UPWARD ，则std::rint等同于std::ceil 。
FE_TOWARDZERO, then std::rint is equivalent to std::trunc.
FE_TOWARDZERO ，则std::rint等同于std::trunc 。
FE_TONEAREST, then std::rint differs from std::round in that halfway cases are rounded to even rather than away from zero.
FE_TONEAREST ，然后std::rint与std::round不同，因为中途情况下的值四舍五入为偶数而不是远离零。

C++ equivalent of above C# code is below, using std::rint.

下面是使用std::rint C ++代码的C ++等效代码。

int x = (int)std::rint(1.5);      // x == 2
int y = (int)std::rint(2.5);      // y == 2

32位浮点格式 (32-Bit Floating-Point Format)

In this guide, we focus on single-precision (32-bit) float. Everything covered, applies to other precision float where information can easily adjust with the table found at the end of this section.

在本指南中，我们重点介绍单精度(32位)浮点数。涵盖的所有内容均适用于其他精密浮子，其中的信息可以通过本节末尾的表格轻松进行调整。

A single-precision format has one sign bit, 8-bit exponent and 23-bit mantissa. The value is negative when the sign bit is set. To get the true exponent, subtract exponent bias(127) from the raw exponent. In the raw exponent, 0(all zeroes) and 255(all ones) are reserved, valid range comprises of 1 to 254. The mantissa for normalized number(as opposed) has a hidden bit which is not stored. So we could infer mantissa has in fact 24-bits of precision. How do we get zero when hidden bit is always 1? Zero is a special number when both the raw exponent and mantissa are zero.

单精度格式具有一个符号位，8位指数和23位尾数。设置符号位时，该值为负。为了获得真实的指数，从原始指数中减去指数偏差( 127 )。在原始指数中，保留0 (全零)和255 (全零)，有效范围包括1到254 。归一化数字的尾数(相对)具有一个未存储的隐藏位。因此，我们可以推断出尾数实际上具有24位精度。当隐藏位始终为1时，如何得到零？当原始指数和尾数均为零时，零是一个特殊数字。

This is the formula for converting the components into a floating-point value.

这是用于将组件转换为浮点值的公式。

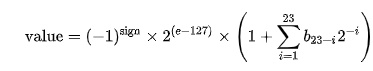
Let's see what the dissector display for the exponent of 0.25, 0.5 and 1.0. Do note that hidden mantissa bit is on.

让我们来看看解剖显示为指数0.25 ， 0.5和1.0 。请注意，隐藏的尾数位已打开。

FloatDissector f = new FloatDissector(0.25f);
f.Display();
f.SetFloatPoint(0.5f);
f.Display();
f.SetFloatPoint(1.0f);
f.Display();

Output of the above code is shown below. Take note the exponent is in radix 2, not 10: M * 2^e. So 1 * 2^-2 would give 0.25. And 1 * 2^-1 = 0.5 and 1 * 2⁰ = 1.

上面代码的输出如下所示。请注意，指数位于基数2中，而不是10：M * 2 ^e 。所以1 * 2 ^-2将得到0.25。并且1 * 2 ^-1 = 0.5和1 * 2 ⁰ = 1。

Sign:Positive, Adjusted Exponent:-2, Raw Exponent:01111101, Mantissa:00000000000000000000000, Float Point Value:0.25

Sign:Positive, Adjusted Exponent:-1, Raw Exponent:01111110, Mantissa:00000000000000000000000, Float Point Value:0.5

Sign:Positive, Adjusted Exponent:0, Raw Exponent:01111111, Mantissa:00000000000000000000000, Float Point Value:1

As the number gets larger as shown, mantissa precision remains constant(2²³=8,388,608), we can say the precision actually becomes lesser. The number of floats from 0.0 ...

如图所示，随着数字的增加，尾数精度保持不变(2 ²³ = 8,388,608)，可以说精度实际上变小了。浮点数从0.0 ...

...to 0.1 = 1,036,831,949
...到0.1 = 1,036,831,949
...to 0.2 = 8,388,608
...到0.2 = 8,388,608
...to 0.4 = 8,388,608
...到0.4 = 8,388,608
...to 0.8 = 8,388,608
...到0.8 = 8,388,608
...to 1.6 = 8,388,608
...到1.6 = 8,388,608
...to 3.2 = 8,388,608
...到3.2 = 8,388,608

Between 0.0 and 0.1, there is more floats because subnormal is included with normal number. Subnormal are small numbers very close to zero.

在0.0到0.1 ，会有更多的浮点数，因为正常数包括了次正规量。次正规量是非常接近零的小数字。

Now let's play around mantissa bits to see how it works. As we proceed from MSB to LSB, each bit value is halved from its preceding bit value. If the MSB or hidden bit has the value of 1, its next bit is 1/2 and the 3rd bit is 1/4. If we set those 2 bits to one, we should get 1 + 0.5 + 0.25 = 1.75

现在，让我们来处理尾数位以了解其工作原理。当我们从MSB转到LSB时，每个位值都从其前一个位值减半。如果MSB或隐藏位的值为1 ，则其下一位为1/2 ，而第三位为1/4 。如果将这两个位设置为1，我们将得到1 + 0.5 + 0.25 = 1.75

FloatDissector f = new FloatDissector(1.0f);
f.SetMantissa(0x3 << 21); // shift binary 11 to the left 21 times.
f.Display();

The output is as we expected.

输出与我们预期的一样。

Sign:Positive, Adjusted Exponent:0, Raw Exponent:01111111, Mantissa:11000000000000000000000, Float Point Value:1.75

However, the hidden bit value is not always 1. It depends on the exponent. When the exponent is -1, it is 1*2^-1=0.5!

但是，隐藏位值并不总是1 。这取决于指数。指数为-1时为1 * 2 ^-1 = 0.5！

If we set those 2 bits again, we should get 0.5 + 0.25 + 0.125 = 0.875

如果我们再次设置这两个位，我们应该得到0.5 + 0.25 + 0.125 = 0.875

FloatDissector f = new FloatDissector(0.5f);
f.SetMantissa(0x3 << 21); // shift binary 11 to the left 21 times.
f.Display();

We are right again!

我们又是对的！

Sign:Positive, Adjusted Exponent:-1, Raw Exponent:01111110, Mantissa:11000000000000000000000, Float Point Value:0.875

The size of fields in each floating-point type is shown together with their significant digit precision.

显示每种浮点类型的字段大小及其有效的数字精度。

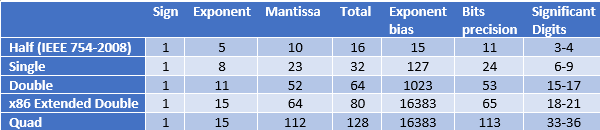
零 (Zero)

IEEE 754 floating-point has 2 distinct zero: positive and negative. A positive zero is indicated by all the bits, including the sign bit, unset. That is why, in a structure with Plain Old Data (POD) types of integer and float type, it is possible, using memset() to quickly zero-initialize every member.

IEEE 754浮点具有2个不同的零：正数和负数。所有未设置的位(包括符号位)指示正零。这就是为什么在具有整数和浮点类型的普通旧数据(POD)类型的结构中，可以使用memset()快速对每个成员进行零初始化。

次普通(下溢) (Subnormal (Underflow))

Subnormal, also known as denormalized number, are IEEE 754 mechanism to deal with very small numbers close to zero. Subnormal are indicated by all zero exponent and non-zero mantissa. With normal number, the mantissa has an implied leading one bit. But with subnormal, the leading 1-bit is not assumed, so subnormal has 1-bit less mantissa precision now (23-bit precision). With the raw exponent set to zero, the true (adjusted) exponent is 0 - 127 which yields -127. The smallest positive subnormal number is when the mantissa is all zeroes except for the Least Significant Bit(LSB), which is approximate to 1.4012984643 × 10⁻⁴⁵ while the smallest positive normal number is approximately 1.1754943508 × 10⁻³⁸.

次规范，也称为非规范化数字，是IEEE 754机制，用于处理非常小的接近零的数字。次零均由所有零指数和非零尾数表示。对于正常数字，尾数具有隐含的前一位。但是对于次标准，不假定前导1位，因此次标准现在的尾数精度降低了1位(23位精度)。在原始指数设置为零的情况下，真实(调整后)指数为0 - 127 ，得出-127 。最小正子范数是尾数全为零时，除了最低有效位(LSB)大约为1.4012984643×10 ^-45 ，最小正正规数为1.1754943508×10 ^-38 。

次常规在英特尔处理器上要慢得多 (Subnormal are much slower on Intel processor)

If you search on Stack Overflow for questions on subnormal, you will no doubt come across this thread which shows subnormal calculations are much slower on Intel architecture processor because normalized number arithmetic is implemented in hardware while subnormal one has to take the slow microcode path. Unless you are dealing with very small, close to zero numbers, you can safely ignore this performance issue. If you are in the other camp, using C++ and SIMD, you have 2 options.

如果您在Stack Overflow上搜索有关次规范的问题，那么无疑会遇到该线程，这表明在Intel体系结构处理器上次规范的计算要慢得多，因为归一化数字算法是在硬件中实现的，而次规范则必须采用缓慢的微码路径。除非您要处理非常小的，接近零的数字，否则可以放心地忽略此性能问题。如果您使用C ++和SIMD在另一个阵营中，则有2个选择。

Use the -ffast-math compiler flag to sacrifice correctness to gain more FP performance. Not recommended.
使用-ffast-math编译器标志来牺牲正确性，以获得更多的FP性能。 不建议。
- Flush-to-zero : treat subnormal outputs as 0
  归零：将次正规输出视为0
- Denormals-to-zero : treat subnormal inputs as 0
  非零归零：将非正态输入视为0

There are 2 ways to do the 2nd option. First one is to set control and status register(CSR) via the Intel Intrinsic, _mm_setcsr() but this method requires you to remember the hexadecimal number(0x8040) to or the bits with existing CSR.

有两种方法可以执行第二个选项。第一个是通过Intel Intrinsic _mm_setcsr()设置控制和状态寄存器(CSR)，但是此方法要求您记住16进制数( 0x8040 ) or具有现有CSR的位。

_mm_setcsr(_mm_getcsr() | 0x8040);

A better method is to call _MM_SET_FLUSH_ZERO_MODE and _MM_SET_DENORMALS_ZERO_MODE() with _MM_FLUSH_ZERO_ON and _MM_DENORMALS_ZERO_ON respectively.

更好的方法是分别通过_MM_FLUSH_ZERO_ON和_MM_DENORMALS_ZERO_ON调用_MM_SET_FLUSH_ZERO_MODE和_MM_SET_DENORMALS_ZERO_MODE() 。

_MM_SET_FLUSH_ZERO_MODE(_MM_FLUSH_ZERO_ON);
_MM_SET_DENORMALS_ZERO_MODE(_MM_DENORMALS_ZERO_ON);

What about x87 Floating-Point Unit(FPU)? Unfortunately, there is no x87 FPU functionality to treat subnormal as zero.

x87浮点单元(FPU)怎么样？不幸的是，没有x87 FPU功能可以将次正常视作零。

无限(溢出) (Infinity (Overflow))

1/0

When any greater than zero number is divided by zero, you get infinity, not divide-by-zero exception. That exception is for integer divide-by-zero. Infinity is indicated all ones exponent and all zeroes mantissa. As with zero number, you have both positive and negative infinity.

当任何大于零的数字除以零时，您将得到无穷大，而不是被零除的异常。该例外是整数除零。无穷表示所有的指数和所有零的尾数。与零数字一样，您同时具有正无穷大和负无穷大。

You can assign Infinity by .NET's Single.PositiveInfinity or Single.NegativeInfinity field and Double.PositiveInfinity or Double.NegativeInfinity field in C# or std::numeric_limits<t>::infinity() defined in limits header in C++11 or using dissector's SetInfinity() method.

您可以通过.NET的Single.PositiveInfinity或Single.NegativeInfinity字段以及C＃中的Double.PositiveInfinity或Double.NegativeInfinity字段或在C ++ 11的limits头文件中定义的std :: numeric_limits <t> :: infinity()来分配Infinity或使用解剖器的SetInfinity()方法。

To test for infinity, if you are using C#, call Single.IsInfinity() and Double.IsInfinity(). If you are on C++11, call std::isinf().

要测试无穷大，如果使用的是C＃，请调用Single.IsInfinity()和Double.IsInfinity() 。如果您使用的是C ++ 11，请调用std :: isinf() 。

Rules for infinity correspond to common sense. See below.

无穷大的规则与常识相对应。见下文。

6 + infinity = infinity
6 / infinity = 0

不是数字 (Not a Number)

0/0

Not a Number(NaN) is what you get when you divide a zero by zero or do a square root on -1. There are 2 types of NaN: quiet and signalling but we are not covering them here. You can assign NaN by .NET's Single.NaN and Double.NaN field in C# or std::nan() defined in cmath header in C++11 or using dissector's SetNaN() method.

当您将零除以零或在-1上-1平方根时，得到的不是数字( NaN )。 NaN有2种类型：静默和信号通知，但我们不在此介绍。您可以通过.NET的C＃中的Single.NaN和Double.NaN字段或在C ++ 11的cmath标头中定义的std :: nan()或使用解剖器的SetNaN()方法来分配NaN 。

Never test for NaN by testing for equality with another NaN. When you compare 2 NaN, the equality test shall return false, even when the 2 NaN in question are exactly the same in binary. If you are using C#, call Single.IsNaN() and Double.IsNaN(). If you are on C++11, call std::isnan().

决不测试NaN通过测试与另一平等NaN 。比较2 NaN时，即使所讨论的2 NaN二进制形式完全相同，相等性测试也应返回false。如果使用的是C＃，请调用Single.IsNaN()和Double.IsNaN() 。如果您使用的是C ++ 11，请调用std :: isnan() 。

Rules for NaN also correspond to common sense. See below.

NaN规则也符合常识。见下文。

NaN + anything = NaN
NaN * anything = NaN

摘要图 (Summary Chart)

The chart summaries the corresponding exponent and mantissa that constitute the floating-point values (like Subnormal, NaN and Infinity).

该图表汇总了构成浮点值的相应指数和尾数(如Subnormal， NaN和Infinity)。

Different combo of Mantissa and Exponent

浮点异常 (Floating-Point Exception)

C# as a language does not expose floating-point exception. Do not even think of circumventing this limitation with P/Invoke to change the FPU status because the .NET Framework and 3rd party libraries rely on the FPU in certain state.

C＃作为一种语言不会公开浮点异常。甚至不要考虑通过P / Invoke来更改FPU状态来规避此限制，因为.NET Framework和第三方库在某些状态下依赖FPU。

On Microsoft C++, it is possible to catch floating-point exception via Structured Exception Handling(SEH) after enabling the FP exception through the _controlfp_s. By default, all FP exceptions are disabled. SEH style exception can be translated to C++ typed exceptions through _set_se_translator. For those who shun proprietary technology and write cross-platform Standard C++ code, read on. As noted on this cppreference page on C++11 floating-point environment. The floating-point exceptions are not related to the C++ exceptions. When a floating-point operation raises a floating-point exception, the status of the floating-point environment changes, which can be tested with std::fetestexcept, but the execution of a C++ program on most implementations continues uninterrupted.

在Microsoft C ++上，可以通过_controlfp_s启用FP异常后，通过结构化异常处理 (SEH)捕获浮点异常。默认情况下，所有FP异常均被禁用。 SEH样式异常可以通过_set_se_translator转换为C ++类型的异常。对于那些避开专有技术并编写跨平台标准C ++代码的人，请继续阅读。如在C ++ 11浮点环境的cppreference页面上所指出的。 浮点异常与C ++异常无关。 当浮点操作引发浮点异常时，浮点环境的状态会更改，可以使用std::fetestexcept进行测试，但是大多数实现上C ++程序的执行不会中断。

平等测试 (Equality Test)

Never test floating-point for equality. Guess the output below!

永远不要测试浮点数是否相等。猜猜下面的输出！

float a = 1.3f;
float b = 1.4f;
float total = 2.7f;
float sum = a + b;
if (sum == total)
    Console.WriteLine("Same");
else
{
    Console.WriteLine("Different");
    Console.WriteLine("{0:G9} != {1:G9}", sum, total);
}
Console.WriteLine("a: {0:G9}", a);
Console.WriteLine("b: {0:G9}", b);

The reason they are not equal because single precision cannot represent 1.3 and 1.4 perfectly. Although changing the type to double precision solves the problem in this case, all floating-point type inherently has this imprecise problem therefore they should not be used as keys in a dictionary (or a std::map in C++ case). The only time equality test poses no problem are the numbers involved, are not result of any computation but directly assignment of literal constant.

它们之所以不相等是因为单精度不能完美地表示1.3和1.4 。尽管在这种情况下将类型更改为双精度可以解决问题，但是所有浮点类型本来就具有这种不精确的问题，因此不应将它们用作字典中的键(或在C ++情况下用作std::map )。唯一一次相等性测试没有问题的是所涉及的数字，不是任何计算的结果，而是直接分配文字常量。

Different
2.69999981 != 2.70000005
a: 1.29999995
b: 1.39999998

Always test floating-point for nearness. Choose an epsilon value a bit larger than your largest error. There is no one-size-fits-all epsilon to use for all cases. For example, the epsilon is set to 0.0000001 and the 2 numbers are actually 0.000000008 and 0.000000005, the test will always pass, so clearly the chosen epsilon is wrong! Nearness test do not have the transitive property as equality test. For instance, a==b and b==c, does not necessarily mean a==c. See the example below.

始终测试浮点是否接近。选择一个比最大误差大一点的ε值。没有适用于所有情况的所有尺寸的epsilon。例如，将epsilon设置为0.0000001 ，而2个数字实际上是0.000000008和0.000000005 ，则该测试将始终通过，因此显然选择的epsilon是错误的！接近度测试不具有传递性，如相等性测试。例如， a==b和b==c不一定表示a==c 。请参见下面的示例。

float epsilon = 0.001f;
float a = 1.5000f;
float b = 1.5007f;
float c = 1.5014f;
if (Math.Abs(a - b) < epsilon)
    Console.WriteLine("a==b");
else
    Console.WriteLine("a!=b");

if (Math.Abs(b - c) < epsilon)
    Console.WriteLine("b==c");
else
    Console.WriteLine("b!=c");

if (Math.Abs(a - c) < epsilon)
    Console.WriteLine("a==c");
else
    Console.WriteLine("a!=c");

The output is as follows.

输出如下。

a==b
b==c
a!=c

For C++, do not use std::numeric_limits<t>::epsilon. For C#, do not use Single.Epsilon and Double.Epsilon. Why? Because these epsilon defined the smallest positive value but most of your time, your largest error value is larger than the smallest value, so your nearness test would fail most of time with those standard epsilon.

对于C ++，请勿使用std :: numeric_limits <t> :: epsilon 。对于C＃，请勿使用Single.Epsilon和Double.Epsilon 。为什么？因为这些epsilon定义了最小的正值，但是在您的大部分时间中，所以您的最大误差值大于最小值，因此对于那些标准epsilon，您的接近度测试大多数时候都将失败。

Whenever possible, turn == into >= or <= comparison, that would be more ideal.

只要有可能，将==变成>=或<=比较，那将是更理想的。

其他种类 (Other Types)

固定点 (Fixed-Point)

When the exponent is fixed at certain negative number, there is no need to store it. The fractional part or decimal point is fixed, thus the name: fixed-point as opposed to floating-point. In the same application, it is not unusual to implement different fixed-point types to accommodate precision requirement of certain type of computation. In such application, conversion of floating-point result, from trigonometry or arithmetic function such as sqrt(), to fixed-point is a common practice, as it is not feasible to reimplement all the floating-point math in the standard library in fixed-point. Fixed-point is not made for calculations dealing very large quantity like total number of particles in the universe or very small numbers involving quantum mechanics due to its limited precision range.

当指数固定为某个负数时，无需存储它。小数部分或小数点是固定的，因此名称为：定点而不是浮点。在同一应用中，实现不同的定点类型以适应某些类型的计算的精度要求并不罕见。在这种应用中，将三角函数或算术函数(例如sqrt()的浮点结果转换为定点是一种常见的做法，因为在固定的标准库中重新实现所有浮点数学是不可行的-点。由于其有限的精度范围，定点不用于处理非常大的数量的计算，例如宇宙中的粒子总数或涉及量子力学的非常小的数量。

小数 (Decimal)

In C#, Decimal type in .NET Base Class Library (BCL) can represent numbers in radix 10 perfectly (due to its exponent is in radix 10), is most suitable to store currency for financial calculations without loss of precision. However, it must be noted that calculations with decimal are orders of magnitude slower than floating-point because it is 128-bit type and no hardware support.

在C＃中，.NET基本类库(BCL)中的十进制类型可以完美地表示基数为10的数字(由于其指数位于基数10中)，最适合存储货币以进行财务计算而不会损失精度。但是，必须注意，使用十进制的计算比浮点运算要慢几个数量级，因为它是128位类型的，并且没有硬件支持。

cpp_float (cpp_float)

In the C++ world, Boost is de facto, peer-reviewed, high quality library to go for whenever a C++ task/work needs to get done. cpp_float featured in Boost.Multiprecision library can be used for computations requiring precision exceeding that of standard built-in types such as float, double and long double. For extended-precision calculations, Boost.Multiprecision supplies a template data type called cpp_dec_float. The number of decimal digits of precision is fixed at compile-time via template parameter.

在C ++世界中， Boost是事实上的，经过同行评审的高质量库，可在需要完成C ++任务/工作时使用。 Boost.Multiprecision库中提供的cpp_float可用于要求精度超过标准内置类型(例如float ， double和long double精度的计算。对于扩展精度计算，Boost.Multiprecision提供了名为cpp_dec_float的模板数据类型。精度的小数位数在编译时通过模板参数固定。

拥有 (Posits)

A new approach to floating-point called posits delivering better performance and accuracy, while doing it with fewer bits. Posit could cut the half the number of bits required, leaving more cache and memory for other information. In posit, there is only one zero and NaN value, leaving no ambiguity. And it is meant to be a drop-in replacement for IEEE floating-point with no modification needed to the code. As of the writing time, there is no commodity hardware implementation of posit but it could change in near future. It is an interesting developement to keep our eyes on.

一种新的称为posits的浮点方法可以提供更好的性能和准确性，同时使用更少的位。可能会减少所需位数的一半，从而为其他信息保留更多的缓存和内存。假定，只有一个零和NaN值，没有任何歧义。它是对IEEE浮点的直接替代，无需修改代码。截至撰写本文时，尚无posit的商品硬件实现，但它可能会在不久的将来发生变化。保持关注是一个有趣的发展。