深度学习优化器+公式推导

最新推荐文章于 2023-12-13 00:00:00 发布

eziaowonder

最新推荐文章于 2023-12-13 00:00:00 发布

阅读量853

点赞数 3

分类专栏： python 深度学习文章标签：神经网络深度学习机器学习

本文链接：https://blog.csdn.net/curious_undergather/article/details/111348755

版权

python 同时被 2 个专栏收录

4 篇文章 0 订阅

订阅专栏

深度学习

1 篇文章 0 订阅

订阅专栏

基础优化
待学习
Reference

本人学习记录，侵删，转载请署名

基础优化

$w\,\,=\,\,w\,\,+\,\,\varDelta \,\,w$

花书第8章Optimization for Training Deep Models中对机器学习中的优化器有如下定义:

finding the parameters $\theta$ of a neural network that significantly reduce a cost function $J(\theta)$ ,

which typically includes a performance measure evaluated on the entire training set as well as additional regularization terms

1. GD — 梯度下降

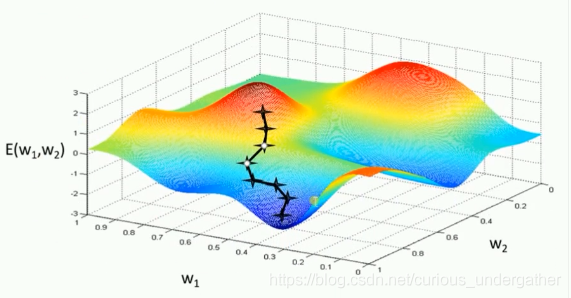
1.1 BGD — 批量梯度下降

BGD

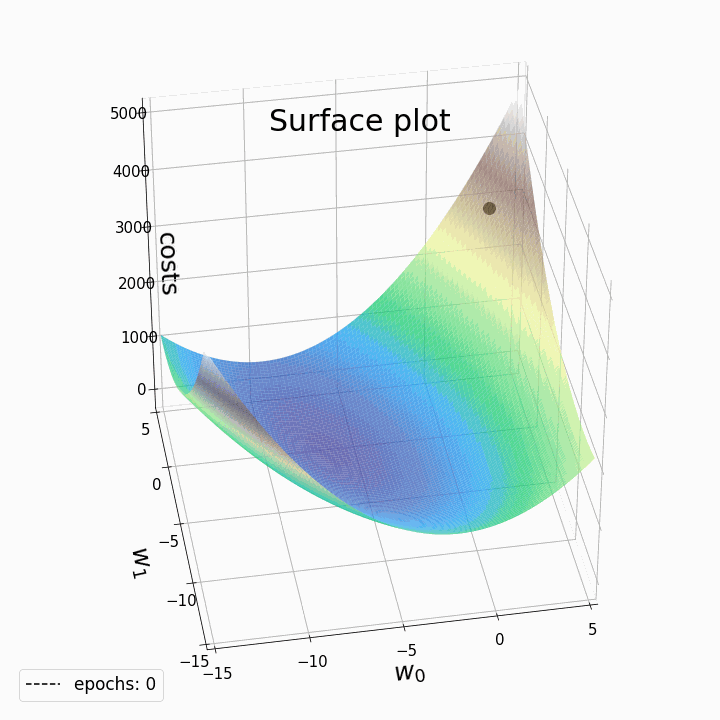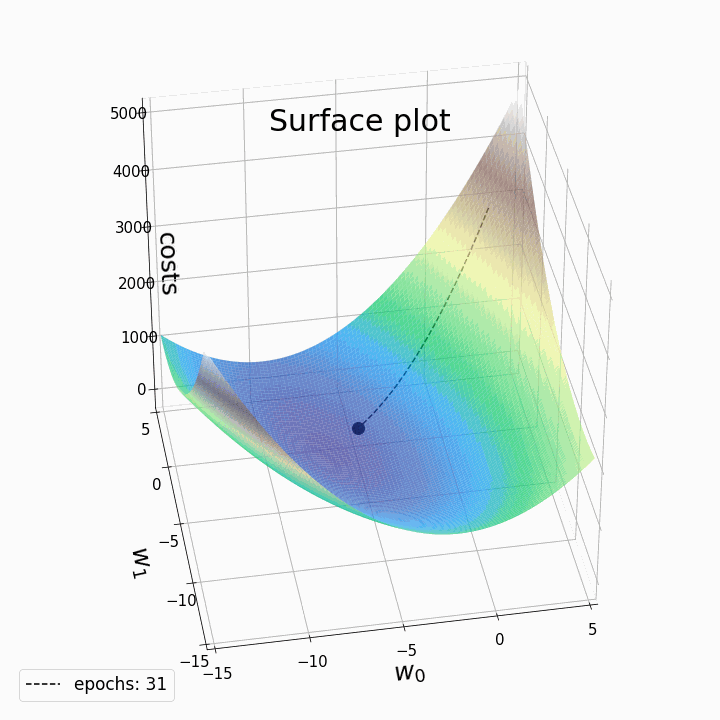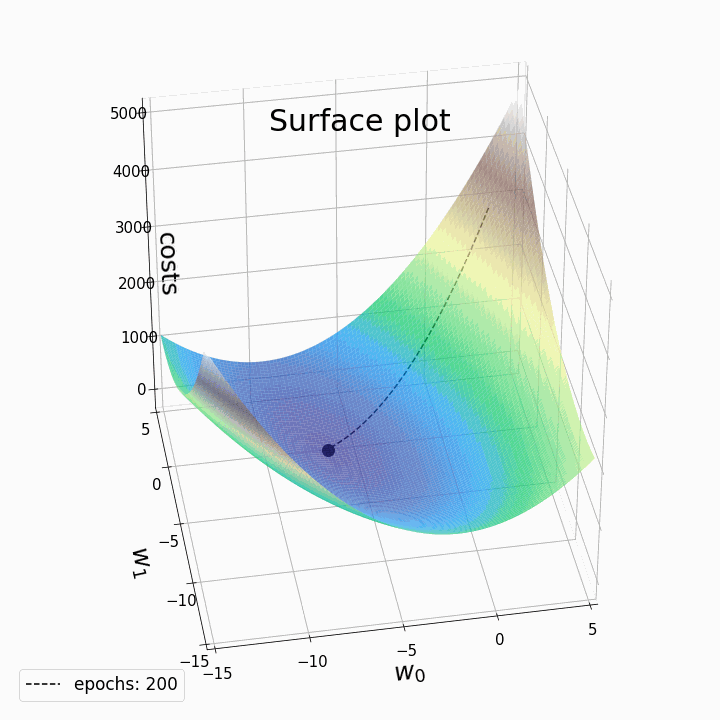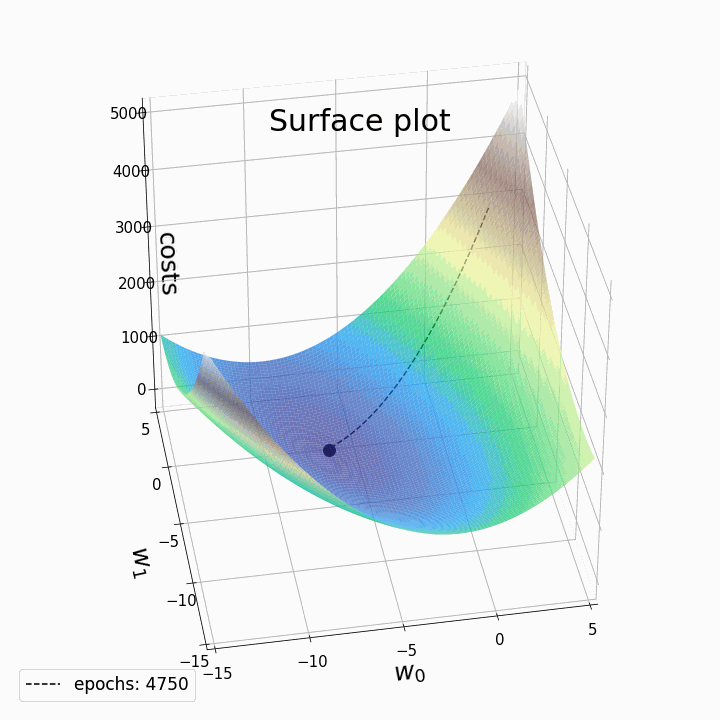
BGD（Batch Gradient Descent）在求解梯度时一次性的将整个数据集进行迭代，从而计算出平均的梯度用于参数的更新

$w_{i+1}=w-\eta \frac{1}{m}\sum_{j=0}^m{\frac{\partial C}{\partial w}_j}$

$m$ 为数据量数， $C$ 为损失函数

优势 — 每次迭代均会往最优化的方向跑，且由于考虑到整个数据集，下降时不会出现震荡
劣势 — 每次优化需遍历整个数据集，时间空间消耗巨大，血亏

代码

1.2 SGD — 随机梯度下降

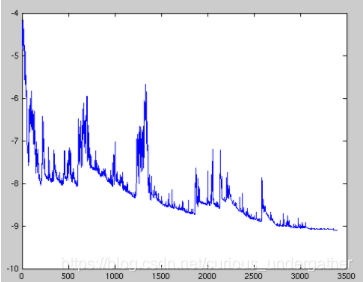
SGD（Stochastic Gradient Descent）— 在每次求解梯度时仅从数据集中随机的选取一个数据点进行梯度计算，从而更新参数

$\Delta w=-\eta J^{\prime}(w) 或 w_{i+1}=w-\eta \frac{\partial C}{\partial w}$
$\eta$ 指学习率， $J^{\prime}$ 指损失关于参数的梯度 ( $\nabla_{w} J(w)$ 也有这种形式) $C$ 为损失函数

其中每次用于更新的数据量为1

优势 — 优化的速度很快

劣势 — 数据中会存在噪音，使得优化朝着并不是最优的方向而迭代. 且还可能使得训练的准确率降低. 但总体还是朝着优化的方向前进的

在这里插入图片描述

代码

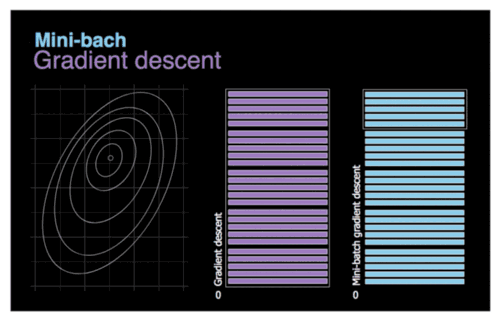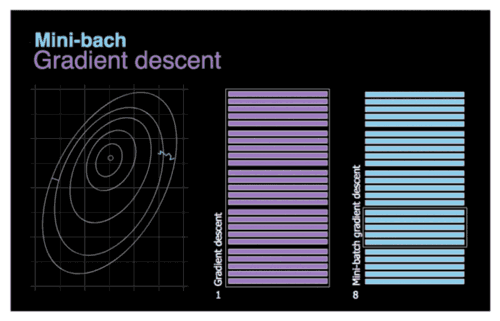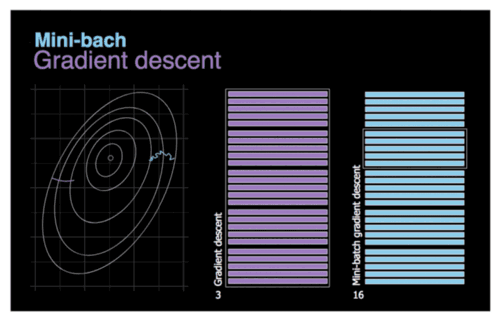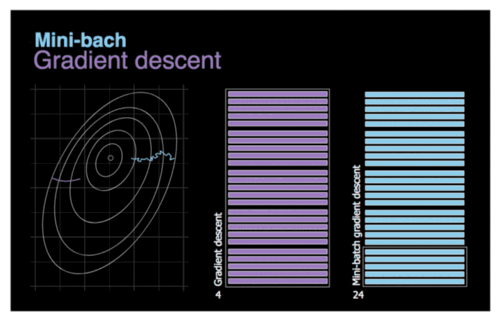
1.3 MBGD — 小批量梯度下降

在这里插入图片描述

$w=w-\eta \cdot \nabla _wJ\left( w;x^{(i:i+n)};y^{(i:i+n)} \right)$

MBGD（Mini-Batch Gradient Descent）将BGD和SGD求一个折中的办法，每次从数据集中选取一小部分的数据进行计算梯度

优势 — 加快梯度下降的迭代速度, 降低数据集中单一噪音数据点对优化的影响

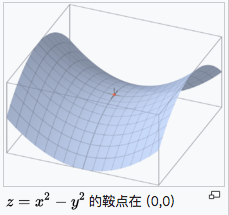
劣势 — 对于鞍点, SGD会在鞍点附近停止更新, 而MSGD会在鞍点周围来回震荡

在这里插入图片描述

代码

2. Momentum

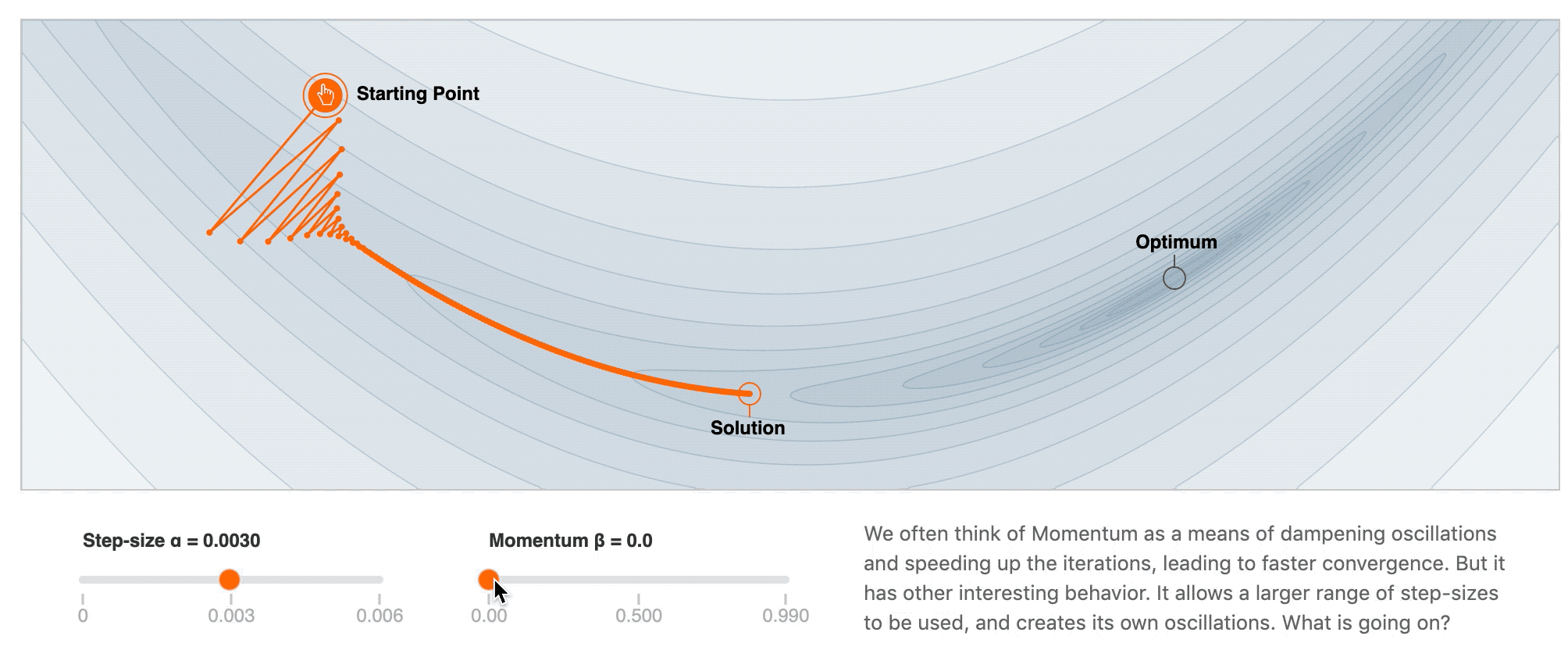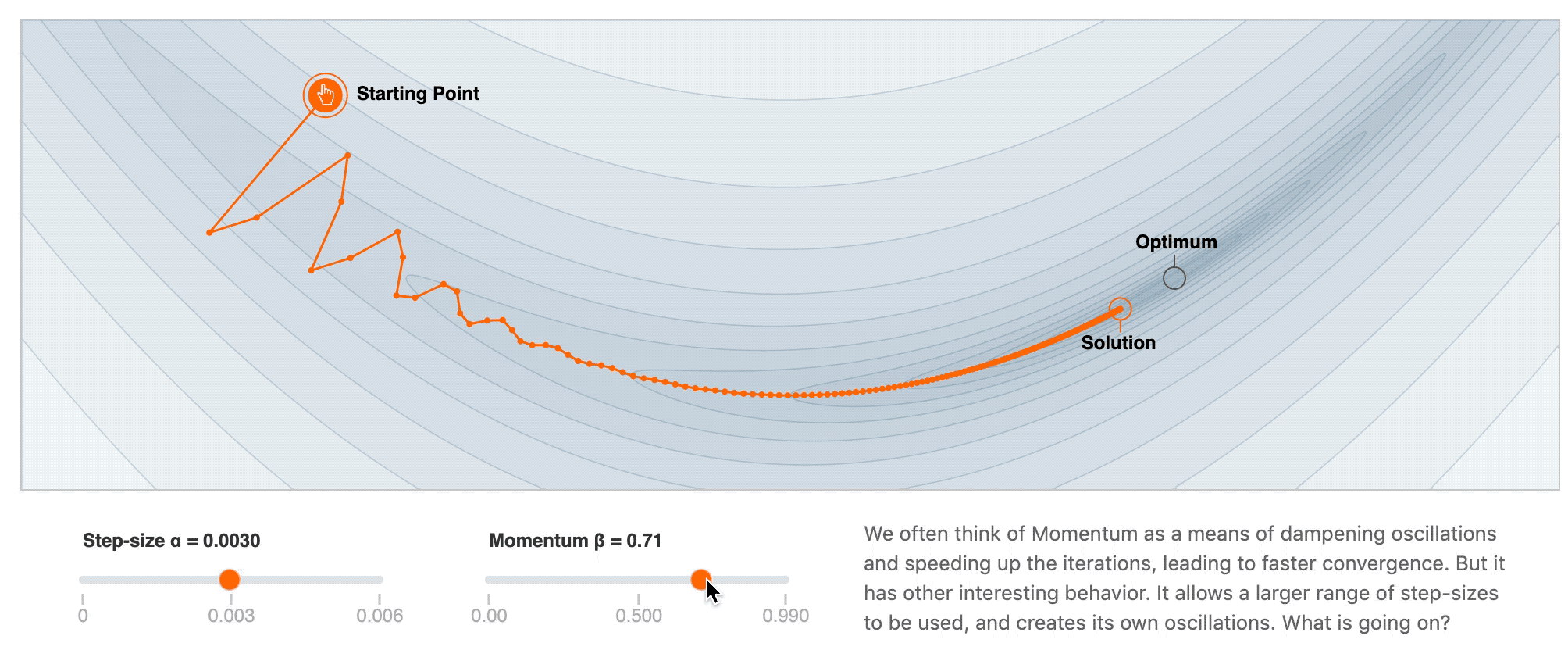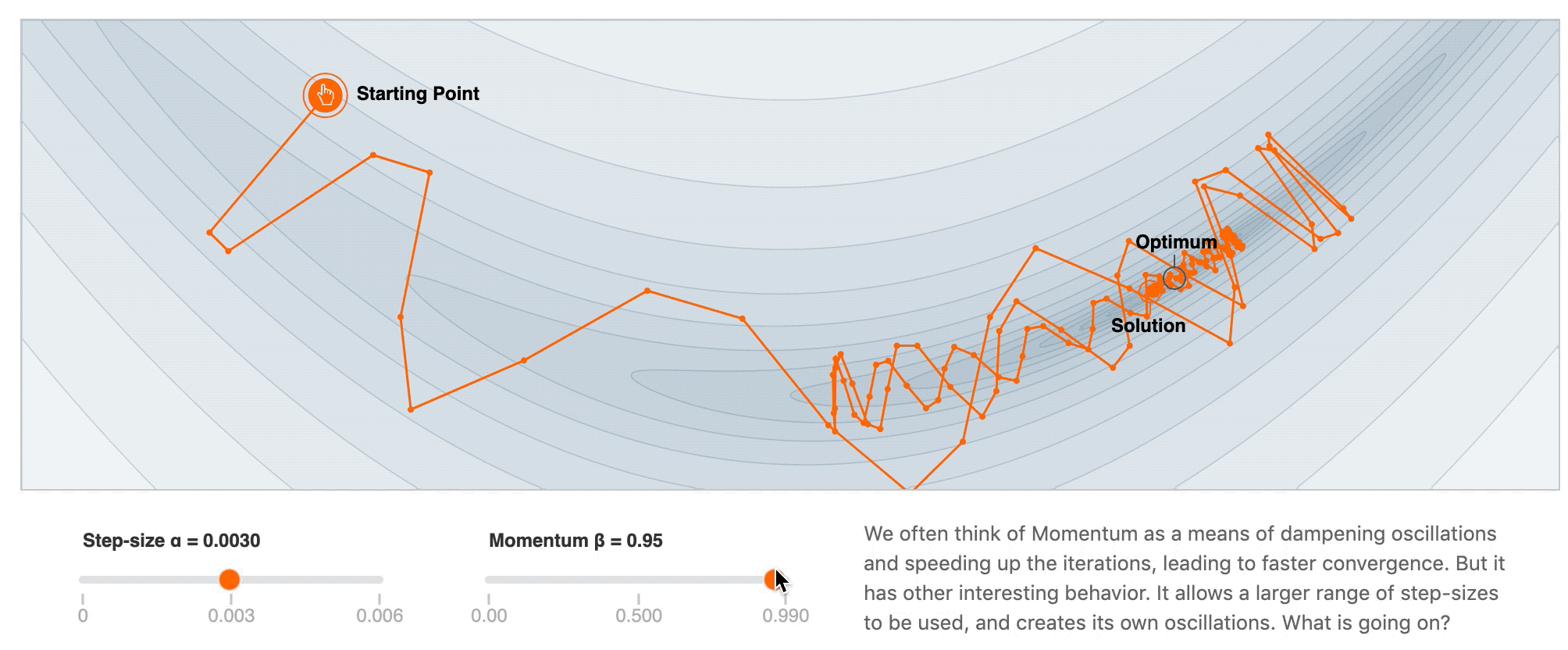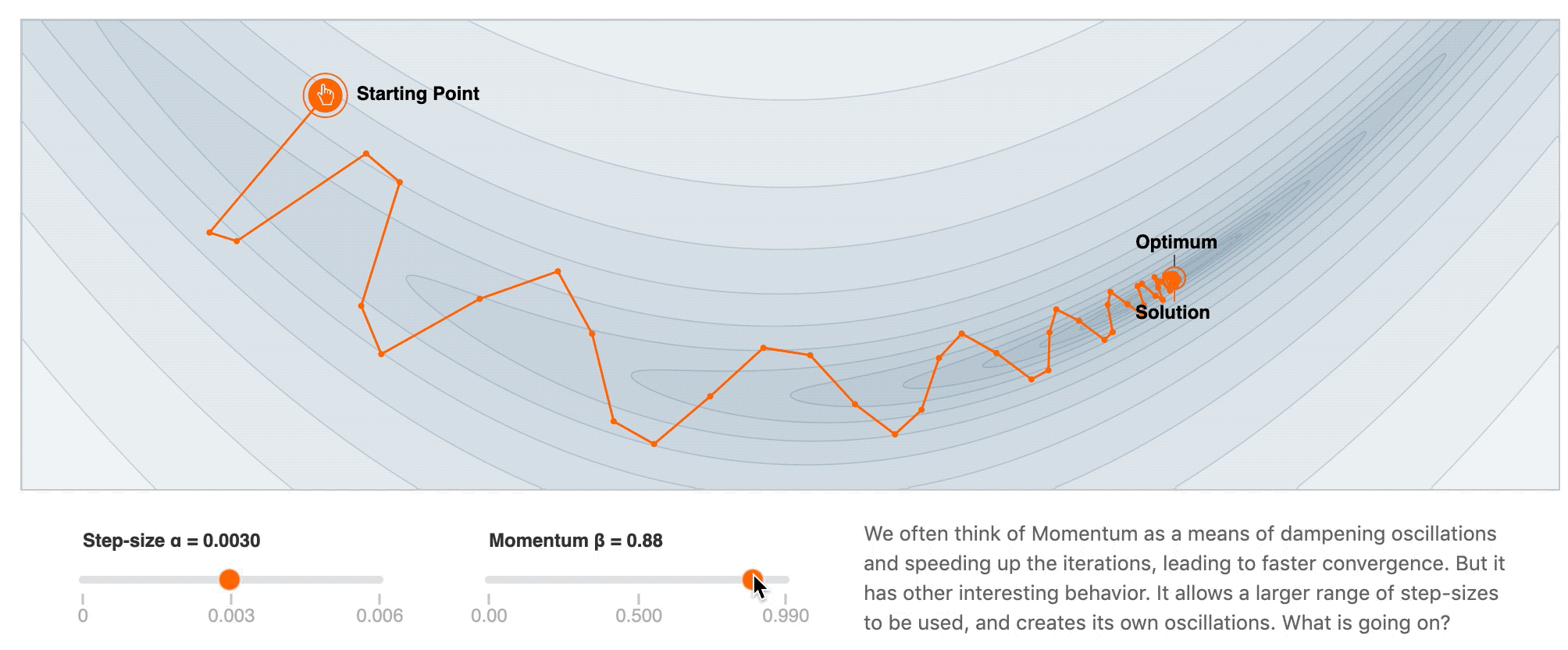
在这里插入图片描述

加速训练过程
解决 SGD 在 ravines 的情况下容易被困住, 就像一个深谷, SGD可能会在两侧左右横跳而达不到低谷

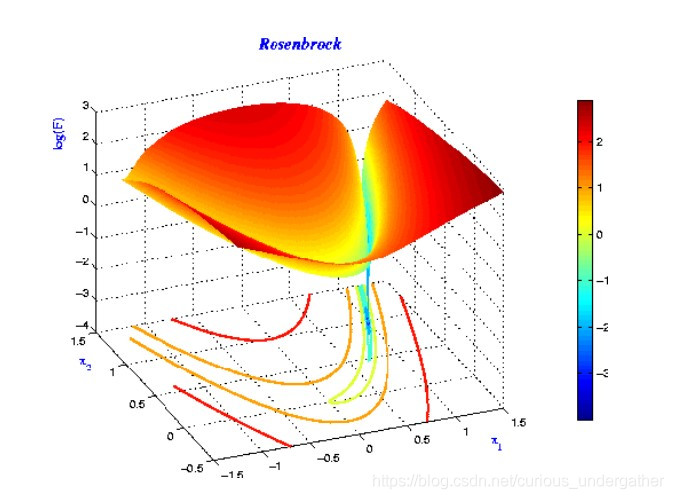
在这里插入图片描述

2.1 Simple momentum update

回顾一下普通的SGD
$\theta=\theta-\eta \nabla_{\theta} J(\theta)$

加了动量后的SGD PLUS！！！
$\begin{array}{l} v_{i}=\gamma v_{i-1}+\eta \nabla_{w} J(w) \\ w=w-v_{i} \end{array}$
这里 $v$ 初始为0, $\gamma$ 为其中一个超参, 一般设定为 $0.9$ (参照上动态图)

优势 — 减少震荡, 跳出 ravines

劣势 — 一定程度上还是比较随机, 只是沿着梯度改变的方向前进

2.2 Nesterov momentum update (Nesterov Accelerated Gradient) (NAG)

$\begin{array}{l} v_{i}=\gamma v_{i-1}+\eta \nabla_{w} J(w - \gamma v_{i-1}) \\ w=w-v_{i} \end{array}$

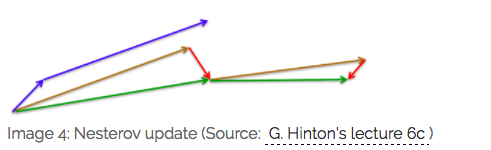
在这里插入图片描述

蓝线是 Momentum 的更新过程，在更新后的累计梯度后有一个明显的大跳跃

棕色线是 NAG 的更新过程，先是一段大跳跃(预测向量)，而后的红线是一段修正向量

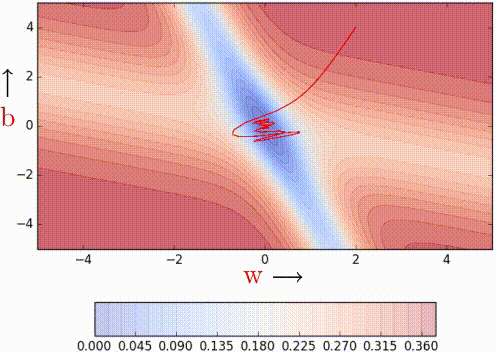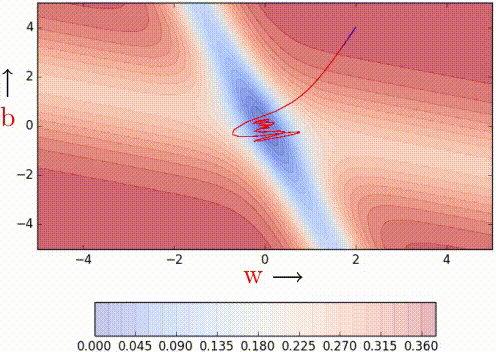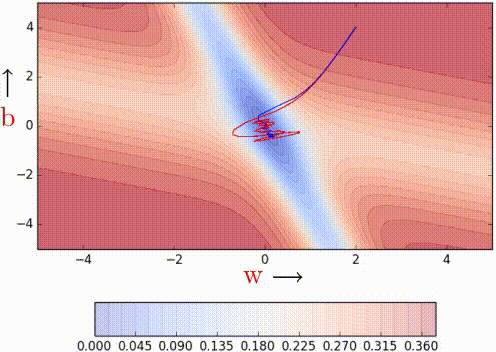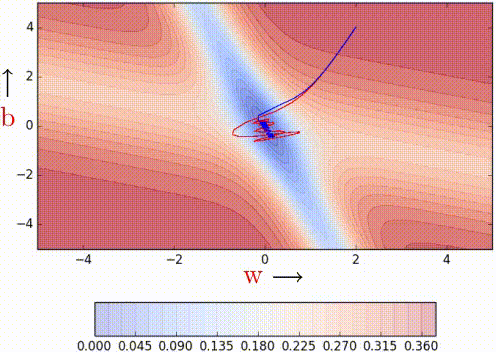
在这里插入图片描述

红线是momentum , 蓝线是NAG

个人觉得这可以在更新梯度时遇到"上坡"前放缓脚步，别直接冲出去了XD

优势 — 更新速度可顺应梯度的变化而改变

劣势 — "学习率"还是一个固定值,

3. Adaptive learning rate optimization algorithm

从训练集中采包含 $m$ 个样本 $\left\{x^{(1)}, \ldots, x^{(m)}\right\}$ 的小批量，对应目标为 $y^{(i)}$

计算梯度
$\boldsymbol{g} \leftarrow \frac{1}{m} \nabla_{\boldsymbol{\theta}} \sum_{i} L\left(f\left(\boldsymbol{x}^{(i)} ; \boldsymbol{\theta}\right), \boldsymbol{y}^{(i)}\right)$

3.1 AdaGrad (Adaptive Subgradient)

在这里插入图片描述

$\begin{aligned} r_{i} &=r_{i-1}+g_{i}^{2} \\ \Delta w &=\frac{\eta}{\epsilon+\sqrt{r_{i}}} g_{i} \\ w &=w-\Delta w \end{aligned}$

其中 $\epsilon$ 是一个极小的正数，用来防止除以0, $g_{i}$ 指在 i 处的梯度, $g_{i}^{2}=g_{i} \odot g_{i}$

$\odot$ 指矩阵的 Hadamard product (哈达玛积), 即 $\left[\begin{array}{cccc} a_{11} b_{11} & a_{12} b_{12} & \cdots & a_{1 n} b_{1 n} \\ a_{21} b_{21} & a_{22} b_{22} & \cdots & a_{2 n} b_{2 n} \\ \vdots & \vdots & & \vdots \\ a_{m 1} b_{m 1} & a_{m 2} b_{m 2} & \cdots & a_{m n} b_{m n} \end{array}\right]$

公式推导:
$r_{i}$ 展开可得：注意，i 从1开始
$\begin{aligned} r_{i} &=r_{i-1}+g_{i}^{2} \\ &=r_{i-2}+g_{i-1}^{2}+g_{i}^{2} \\ &=r_{0}+g_{1}^{2}+g_{2}^{2}+\cdots+g_{i}^{2} \\ &=r_{0}+\sum_{j=1}^{i} g_{j}^{2} \end{aligned}$

一般情况下 $r_{0} = 0$ , 此时

$\begin{aligned} \Delta w &=-\frac{\eta}{\epsilon+\sqrt{r_{1}}} g_{1} \\ &=-\frac{\eta}{\epsilon+g_{1}} g_{1} \end{aligned}$

但本着分母不能为0的原则( $g_{i}$ 不确定)，令 $r_{0} = \epsilon$ , 此时就可以把位于分母处的 $\epsilon$ 这一保险去除了, 递推公式也变成了:

$\begin{aligned} r_{i} &=r_{0}+\sum_{j=1}^{i} g_{j}^{2} \\ &=\epsilon+\sum_{j=1}^{i} g_{j}^{2}>0 \end{aligned}$

可知 $r_{i}$ 恒大于0，因此不必在计算 $\Delta w$ 中额外加入 $\epsilon$

优势 —

具有损失最大偏导的参数相应地有一个快速下降的学习率，而具有小偏导的参数在学习率上有相对较小的下降.净效果是在参数空间中更为平缓的倾斜方向会取得更大的进步. 摘自<花书>
减少了学习率的手动调节

劣势 — 分母会不断积累，这样学习率就会收缩并最终会变得非常小

以下，RMSprop 和 Adadelta 都是为了解决 Adagrad 学习率急剧下降问题所提出的，大致上算同时期的算法

3.2.1 RMSProp – AdaGrad 的 Plus

在这里插入图片描述

$\begin{aligned} r_i&=\rho r_{i-1}+(1-\rho )g_{i}^{2}\\ \Delta w&=-\frac{\eta}{\epsilon +\sqrt{r_i}}g_i\\ w&=w+\Delta w\\ \end{aligned}$

当然也有这个版本的, 一个意思

$\begin{array}{l} E\left[ g^2 \right] _t=\gamma E\left[ g^2 \right] _{t-1}+\left( 1-\gamma \right) g_{t}^{2}\\ \\ \theta _{t+1}=\theta _t-\frac{\eta}{\sqrt{E\left[ g^2 \right] _t+\epsilon}}g_t\\ \end{array}$

$\rho$ 和 $\gamma$ 都是这个算法新引入的超参在不同参考资料中的写法，上面那种是在花书的，下面可能是论文的

一般 $\rho$ 或 $\gamma$ 为 0.9, η 为 0.001

通过引入此超参，使得RMSProp只会累积近期的梯度信息，对于“遥远的历史”会以指数衰减的形式放弃，即指数加权平均法

AdaGrad旨在应用于凸问题时快速收敛.当应用于非凸函数训练神经网络时，学习轨迹可能穿过了很多不同的结构，最终到达一个局部是凸碗的区域.AdaGrad 根据平方梯度的整个历史收缩学习率，可能使得学习率在达到这样的凸结构前就变得太小了.RMSProp 使用指数衰减平均以丢弃遥远过去的历史，使其能够在找到凸碗状结构后快速收敛，它就像一个初始化于该碗状结构的 AdaGrad 算法实例

个人理解：

AdaGrad 在碗里面表现很好，在海浪里表现一般，因记住太久远的东西导致学习率到最后太拉跨.

RMSProp则通过指数加权平均, 仅记住最近的东西，使得能将海浪直接转化成碗, 从而发挥最大功效

通俗理解指数加权平均

3.2.2 Adadelta – AdaGrad 的 Plus

RMSProp更简单好用点，这个计算相对复杂，原理都是相似的

$\begin{aligned} r_i&=\rho r_{i-1}+(1-\rho )g_{i}^{2}\\ s_i&=\rho s_{i-1}+(1-\rho )\Delta w^2\\ \Delta w&=-\frac{\sqrt{\epsilon +s_i}}{\sqrt{\epsilon +r_i}}g_i\\ w&=w+\Delta w\\ \end{aligned}$

同理，上面的是在知乎找的，下面的可能是论文的(看完论文再更新)

初始化：
$E\left[ g^2 \right] _0=0,E\left[ \Delta x^2 \right] _0=0 \\$
具体更新：
$\\ E\left[ g^2 \right] _t=\rho E\left[ g^2 \right] _{t-1}+(1-\rho )g_{t}^{2}\\ \\ \Delta w_t=-\frac{\eta}{\sqrt{E\left[ g^2 \right] _t+\epsilon}}g_t\Rightarrow -\frac{\eta}{RMS[g]_t}g_t\,\,\Rightarrow -\frac{RMS[\Delta w]_{t-1}}{RMS[g]_t}g_t\\ \\ w_{t+1}=w_t+\Delta w_t\\$

$\rho$ 一般为 0.9

这里

$RMS[g]_t=E\left[ g^2 \right] _t+\epsilon$

$RMS[\Delta w]_{t-1}=\rho E\left[ \varDelta w \right] _{t-1}+(1-\rho )\varDelta w_{t-1}$

注意到， $\eta \,\,=\,\,RMS[\Delta w]_{t-1}$ , 即梯度的均方根 root mean squared (RMS)

梯度的均方根 : 将所有值平方求和，求其均值，再开平方，就得到均方根值

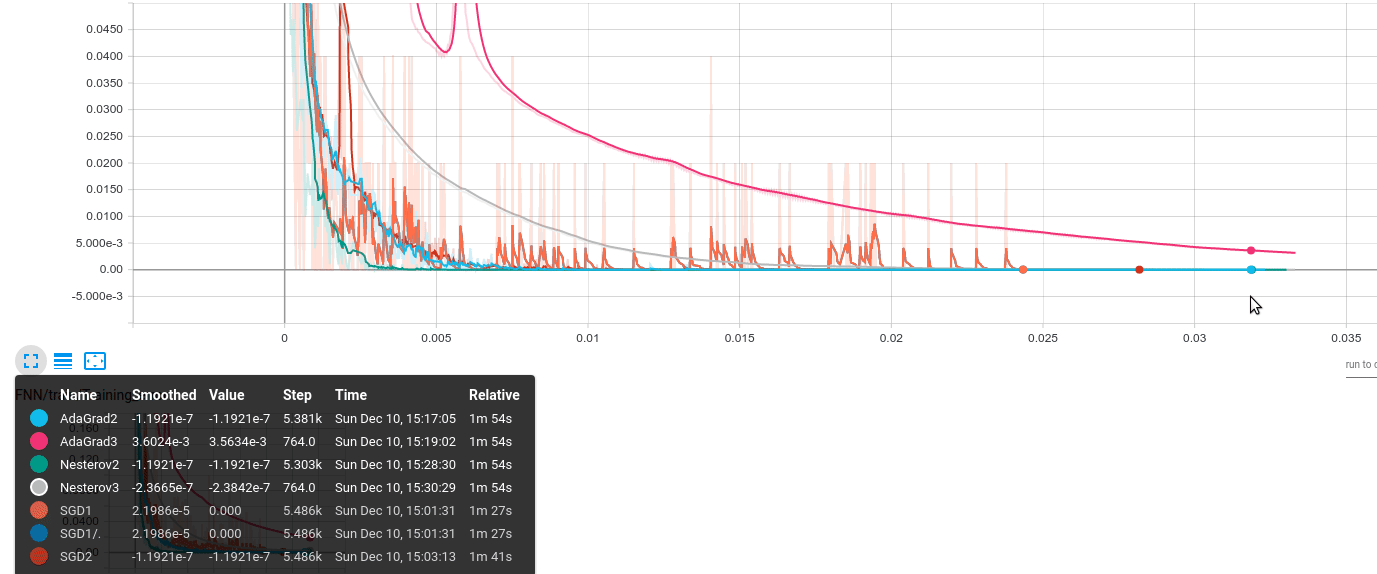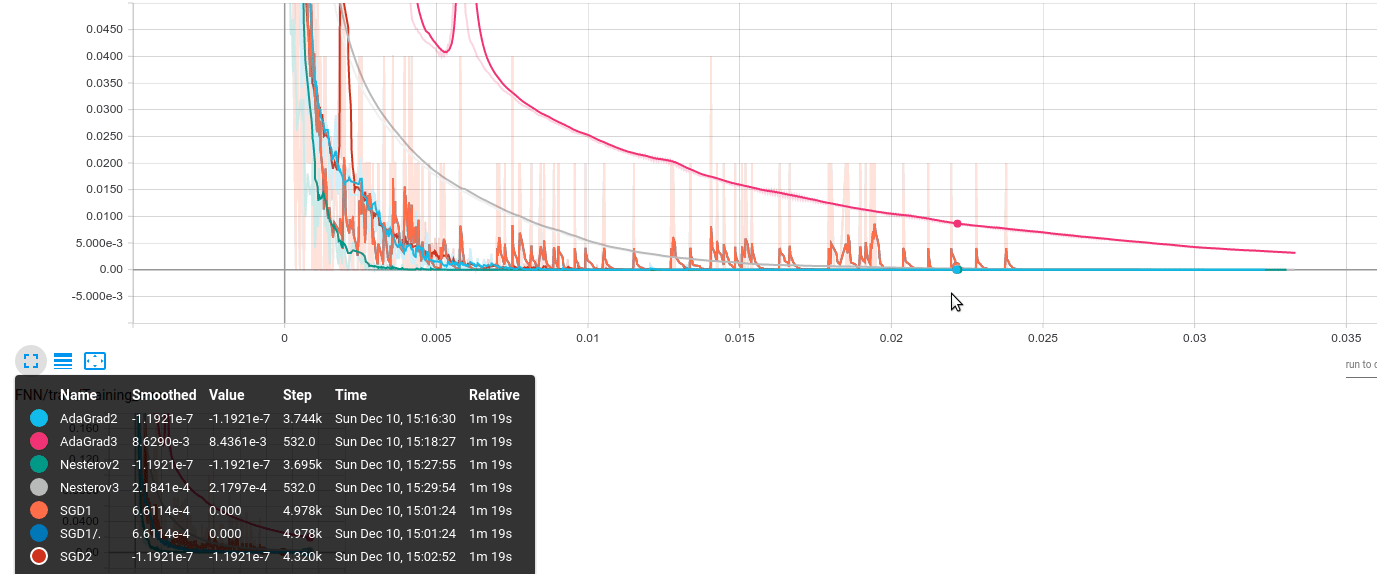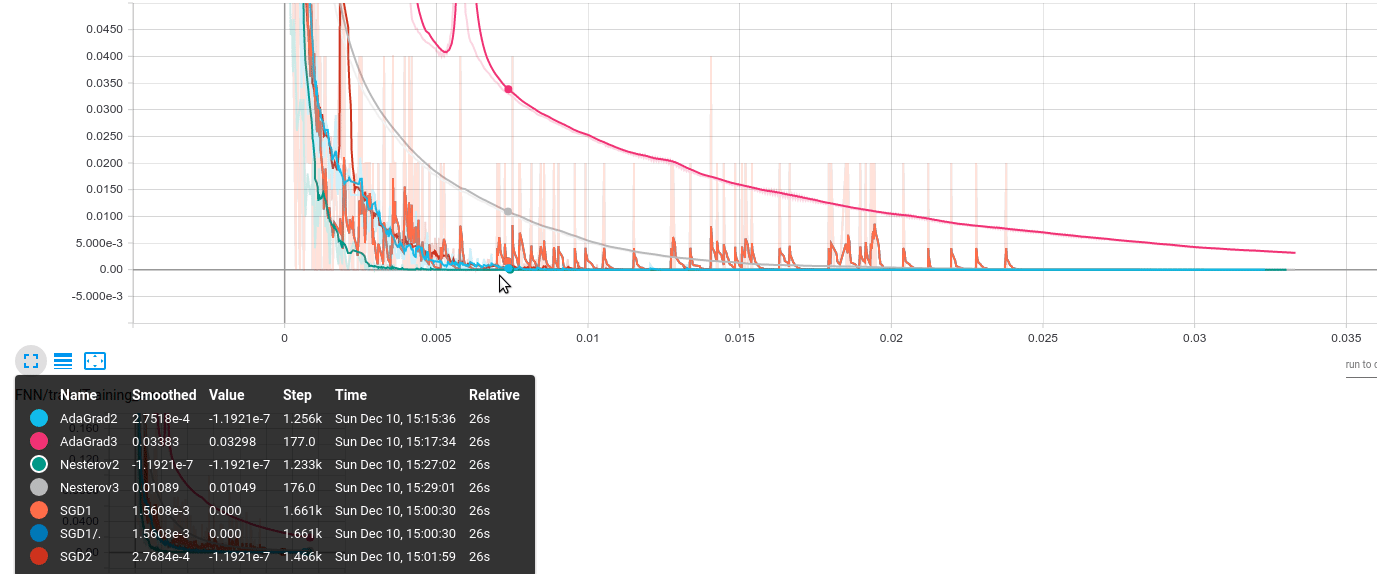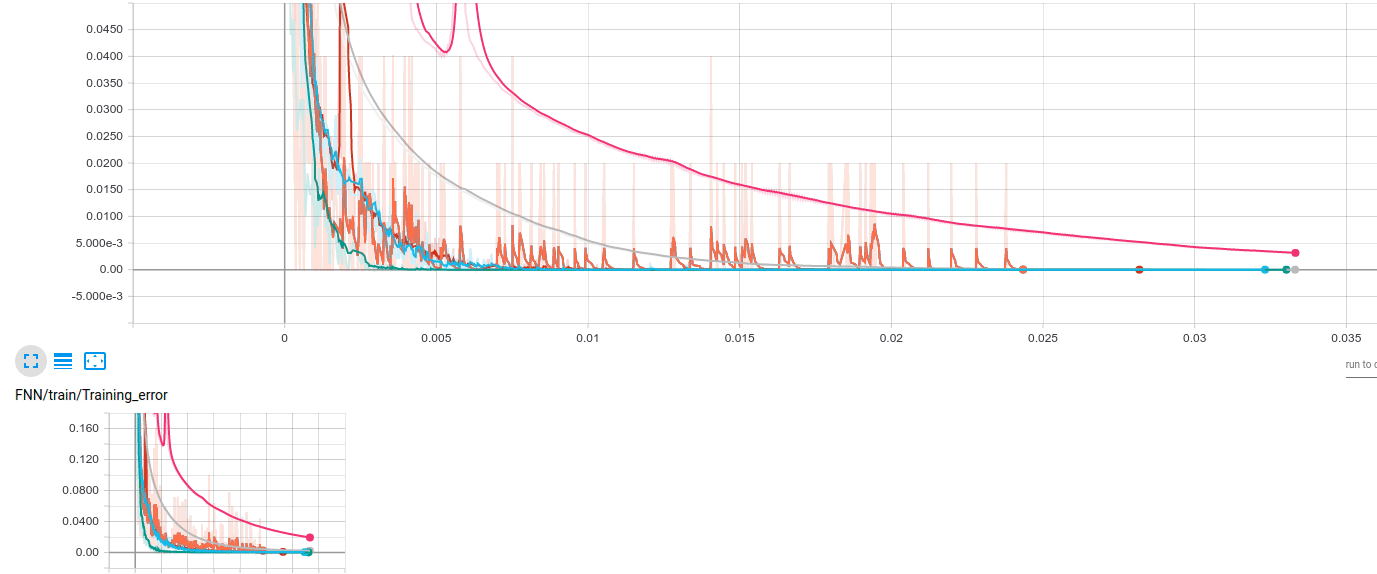
以上算法的比较：

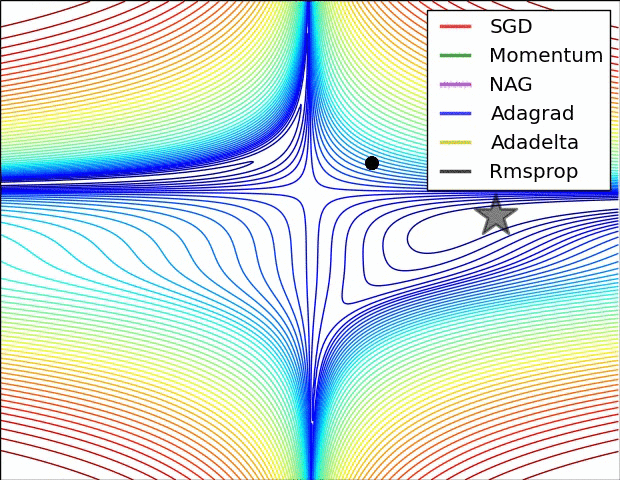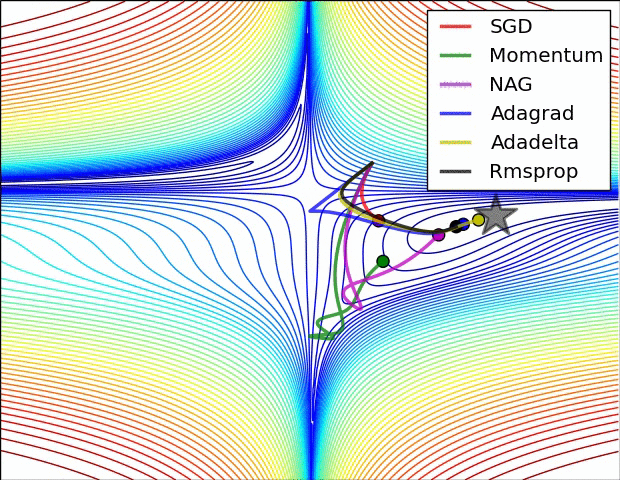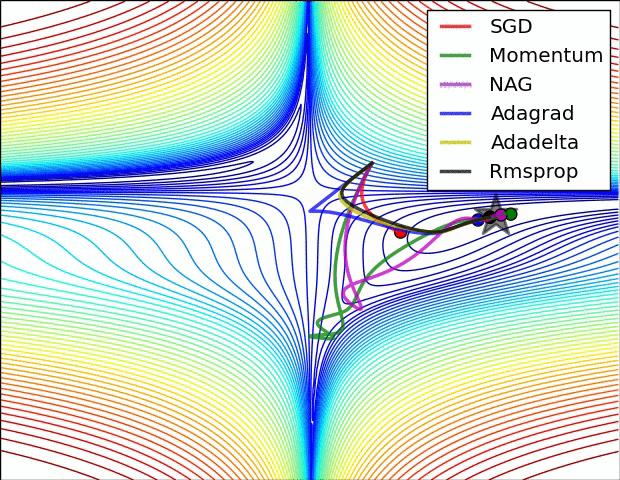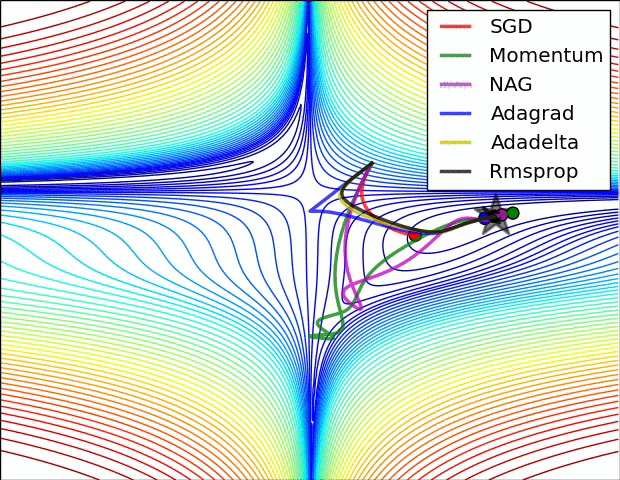
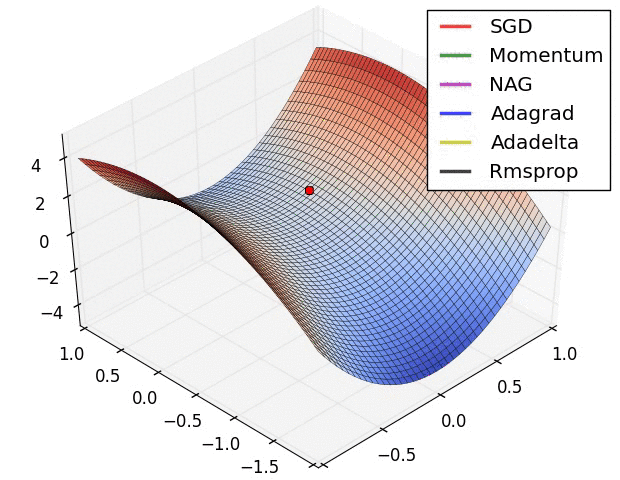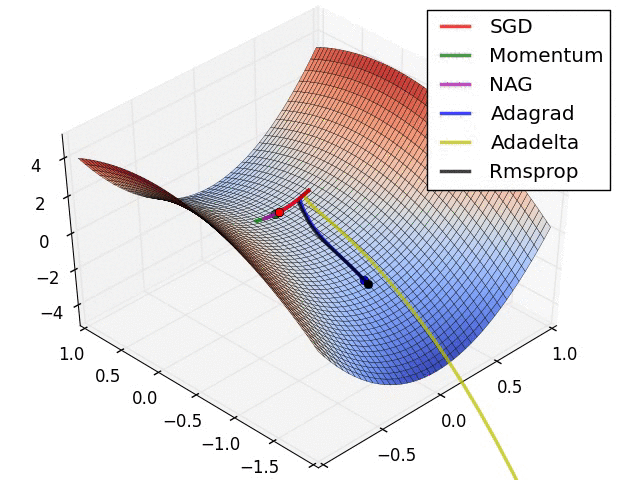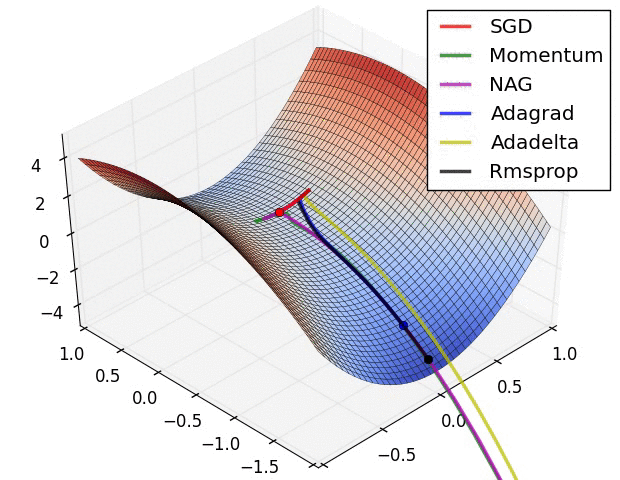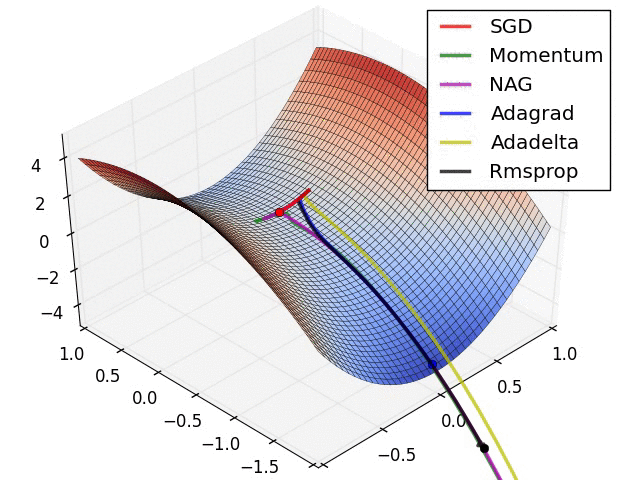
在这里插入图片描述

3.3 Adam：Adaptive Moment Estimation => RMSprop + Momentum

指数加权移动平均——知乎

指数加权移动平均——吴恩达老师的DeepLearning.ai

在这里插入图片描述

$t :$ 更新的步长 (steps)
$\alpha:$ 学习率，用于控制步幅 (stepsize)
$\theta$ : 目标参数
$f(\theta):$ 带有参数 $\theta$ 的随机目标函数, 一般指损失函数
$g_{t}:$ 目标函数 $f(\theta)$ 对 $\theta$ 求导所得梯度
$\beta_{1}:$ 一阶矩衰减系数
$\beta_{2}:$ 二阶矩衰减系数
$m_{t}:$ 梯度 $g_{t}$ 的一阶矩,即梯度 $g_{t}$ 的期望
$v_{t}:$ 梯度 $g_{t}$ 的二阶矩,即梯度 $g_{t}^{2}$ 的期望
$\hat{m}_{t}: m_{t}$ 的偏置矫正,考虑到 $m_{t}$ 在零初始值情况下向0偏置
$\hat{v}_{t}: v_{t}$ 的偏置矫正,考虑到 $v_{t}$ 在零初始值情况下向0偏置

$\begin{array}{l} t\gets t+1\\ g_t\gets \nabla _{\theta}f_t\left( \theta _{t-1} \right) \,\,\\ m_t\gets \beta _1\cdot m_{t-1}+\left( 1-\beta _1 \right) \cdot g_t\\ v_t\gets \beta _2\cdot v_{t-1}+\left( 1-\beta _2 \right) \cdot g_{t}^{2}\\ \hat{m}_t\gets \frac{m_t}{\left( 1-\beta _{1}^{t} \right) \,\,}\\ \widehat{v}_t\gets \frac{v_t}{\left( 1-\beta _{2}^{t} \right)}\\ \theta _t\gets \theta _{t-1}-\alpha \frac{\hat{m}_t}{\left( \sqrt{\hat{v}_t}+\epsilon \right)}\\ \end{array}$

优势

(1). 惯性保持：Adam算法记录了梯度的一阶矩，即过往所有梯度与当前梯度的平均，使得每一次更新时，上一次更新的梯度与当前更新的梯度不会相差太大，即梯度平滑、稳定的过渡，可以适应不稳定的目标函数.

(2). 环境感知：Adam记录了梯度的二阶矩，即过往梯度平方与当前梯度平方的平均，这体现了环境感知能力，为不同参数产生自适应的学习速率.

(3). 超参数具有很好的解释性，且通常无需调整或仅需很少的微调.

3.4 AdaMax

在这里插入图片描述

Adam 作者在Adam论文的extensions部分提出的一个新的算法，他们发现在Adam中，单个权重的更新规则是将其梯度与当前 $\left|g_{t}\right|^{2}$ 和过去梯度 $v_{t-1}$ 的 $\ell_{2}$ 范数（标量）成反比例缩放.
将以下公式推导至 p-范数, 即

$v_t=\beta _2v_{t-1}+\left( 1-\beta _2 \right) \left| g_t \right|^2\,\,\\ \Longrightarrow v_t=\beta _{2}^{p}v_{t-1}+\left( 1-\beta _{2}^{p} \right) \left| g_t \right|^p\,\,=\left( 1-\beta _{2}^{p} \right) \sum_{i=1}^t{\beta _{2}^{p(t-i)}}\cdot \left| g_i \right|^p$

但 p-范数会因较大的p值而在数值上变得不稳定，可一旦 $\rightarrow \infty$ ,一个极其稳定和简单的算法
出现了. 在使用L^p范数情况下，步长t和 $vt^(1/p)$ 成反比.

注意到此时衰减项等价于 $\beta_{2}^{p}$ 而不是 $\beta_{2}$ . 令 $\rightarrow \infty$ , 定义 $u_{t}=\lim _{p \rightarrow \infty}\left(v_{t}\right)^{1 / p}$ , 有：

$\begin{aligned} u_{t}=\lim _{p \rightarrow \infty}\left(v_{t}\right)^{1 / p} &=\lim _{p \rightarrow \infty}\left(\left(1-\beta_{2}^{p}\right) \sum_{i=1}^{t} \beta_{2}^{p(t-i)} \cdot\left|g_{i}\right|^{p}\right)^{1 / p} \\ &=\lim _{p \rightarrow \infty}\left(1-\beta_{2}^{p}\right)^{1 / p}\left(\sum_{i=1}^{t} \beta_{2}^{p(t-i)} \cdot\left|g_{i}\right|^{p}\right)^{1 / p} \\ &=\lim _{p \rightarrow \infty}\left(\sum_{i=1}^{t}\left(\beta_{2}^{(t-i)} \cdot\left|g_{i}\right|\right)^{p}\right)^{1 / p} \\ &=\max \left(\beta_{2}^{t-1}\left|g_{1}\right|, \beta_{2}^{t-2}\left|g_{2}\right|, \ldots, \beta_{2}\left|g_{t-1}\right|,\left|g_{t}\right|\right) \end{aligned}$
(这步还不会… 学会了再来补充)
而后很自然地
$u_{t}=\max \left(\beta_{2} \cdot u_{t-1},\left|g_{t}\right|\right)$

最终

$\begin{aligned} &t\gets t+1\\ &g_t\gets \nabla _wf_t\left( w_{t-1} \right) \,\,\\ &\begin{array}{l} m_t\gets \beta _1\cdot m_{t-1}+\left( 1-\beta _1 \right) \cdot g_t\\ u_t\gets \max \left( \beta _2\cdot u_{t-1},\left| g_t \right| \right) \,\,\\ w_t\gets w_{t-1}-\left( \alpha /\left( 1-\beta _{1}^{t} \right) \right) \cdot m_t/u_t\\ \end{array}\\ \end{aligned}$

建议值:
$\eta | \alpha =0.002, \beta_{1}=0.9, \text { and } \beta_{2}=0.999$

PS:这个max比较的是梯度各个维度上的当前值和历史最大值

补充知识:

对于p-范数，如果
$x=\left[x_{1}, x_{2}, \cdots, x_{n}\right]^{\mathrm{T}}$
那么向量X的p-范数 $\ell_{p}$ 就是
$\|x\|_{p}=\left(\left|x_{1}\right|^{p}+\left|x_{2}\right|^{p}+\cdots+\left|x_{n}\right|^{p}\right)^{\frac{1}{p}}$
$\ell_{1}$ 范数：
$\|x\|_{1}=\left|x_{1}\right|+\left|x_{2}\right|+\left|x_{3}\right|+\cdots+\left|x_{n}\right|$
$\ell_{2}$ 范数：
$\|x\|_{2}=\left(\left|x_{1}\right|^{2}+\left|x_{2}\right|^{2}+\left|x_{3}\right|^{2}+\cdots+\left|x_{n}\right|^{2}\right)^{1 / 2}$

L0范数是指向量中非0的元素的个数(L0范数很难优化求解)

L1范数是指向量中各个元素绝对值之和

L2范数是指向量各元素的平方和然后求平方根

L1范数可以进行特征选择，即让特征的系数变为0

L2范数可以防止过拟合，提升模型的泛化能力，有助于处理 condition number不好下的矩阵(数据变化很小矩阵求解后结果变化很大)

（核心：L2对大数，对outlier离群点更敏感！）

下降速度：最小化权值参数L1比L2变化的快

模型空间的限制：L1会产生稀疏 L2不会.

L1会趋向于产生少量的特征，而其他的特征都是0，而L2会选择更多的特征，这些特征都会接近于0.

4. Nadam => RMSProp + NAG

$\,\, \begin{aligned} \,\, NAG\\ g_t&=\nabla _{w_t}J\left( w_t-\gamma m_{t-1} \right)\\ m_t&=\gamma m_{t-1}+\eta g_t\\ w_{t+1}&=w_t-m_t\\ \end{aligned}\,\, \begin{aligned} \,\, Momentum\\ g_t&=\nabla _{w_t}J\left( w_t \right)\\ m_t&=\gamma m_{t-1}+\eta g_t\\ w_{t+1}&=w_t-m_t\\ \end{aligned}$
$\begin{aligned} \,\, RMSprop\\ r_i&=\rho r_{i-1}+(1-\rho )g_{i}^{2}\\ \Delta w&=-\frac{\eta}{\epsilon +\sqrt{r_i}}g_i\\ w&=w+\Delta w\\ \end{aligned}\,\,$
$\begin{array}{c} \,\,Adam\\ t\,\,\gets \,\,t+1\\ g_t\gets \nabla _{\theta}f_t\left( \theta _{t-1} \right) \,\,\\ m_t\gets \beta _1\cdot m_{t-1}+\left( 1-\beta _1 \right) \cdot g_t\\ v_t\gets \beta _2\cdot v_{t-1}+\left( 1-\beta _2 \right) \cdot g_{t}^{2}\\ \hat{m}_t\gets \frac{m_t}{\left( 1-\beta _{1}^{t} \right) \,\,}\\ \widehat{v}_t\gets \frac{v_t}{\left( 1-\beta _{2}^{t} \right)}\\ \theta _t\gets \theta _{t-1}-\alpha \frac{\hat{m}_t}{\left( \sqrt{\hat{v}_t}+\epsilon \right)}\\ \end{array} \\$

Dozat 提出一个修改NAG的方式：与其两次应用动量优化 $\gamma m_{t-1}$ ，一次是更新 $g_{t}$ ，第二次则是更新 $w_{t+1}$ ，不如直接将预测动量向量应用到当前参数的更新上:

$\begin{aligned} g_{t} &=\nabla_{w_{t}} J\left(w_{t}\right) \\ m_{t} &=\gamma m_{t-1}+\eta g_{t} \\ w_{t+1} &=w_{t}-\left(\gamma m_{t}+\eta g_{t}\right) \end{aligned}$

其中 $\gamma$ 是动量下降项， $\eta$ 是步长(理解成LR也可以)，可以看到现在直接应用 $m_{t}$ 来预测

为了将Nesterov momentum整合进Adam, 可仿效上面的公式，即使用当前的动量 $m_{t}$ 来进行预测，也就是说，只要简单地替换下动量参数即可

Adam公式中的第二条式子展开 PS: $\hat{v}_t$ 不需要改变

$\begin{aligned} m_t&=\beta _1m_{t-1}+\left( 1-\beta _1 \right) g_t\\ \hat{m}_t&=\frac{m_t}{1-\beta _{1}^{t}}\\ w_{t+1}&=w_t-\frac{\eta}{\sqrt{\hat{v}_t}+\epsilon}\hat{m}_t\\ \end{aligned}$

得

$w_{t+1}=w_t-\frac{\eta}{\sqrt{\hat{v}_t}+\epsilon}\left( \frac{\beta _1m_{t-1}}{1-\beta _{1}^{t}}+\frac{\left( 1-\beta _1 \right) g_t}{1-\beta _{1}^{t}} \right)$

而
$\frac{m_{t-1}}{1-\beta _{1}^{t}}\,\,\approx \,\,\frac{m_{t-1}}{1-\beta _{1}^{t-1}}\,\,=\,\,\hat{m}_{t-1}$
(不用在意，反正下一步就换掉了)

则可将公式化简为

$w_{t+1}=w_t-\frac{\eta}{\sqrt{\hat{v}_t}+\epsilon}\left( \beta _1\hat{m}_{t-1}+\frac{\left( 1-\beta _1 \right) g_t}{1-\beta _{1}^{t}} \right)$

然后，前面 $w_{t+1}=w_{t}-\left(\gamma m_{t}+\eta g_{t}\right)$ (的思想) 就派上用场了，直接把 $\hat{m}_{t-1}$ 换为 $\hat{m}_{t}$

最终公式为

$w_{t+1}=w_t-\frac{\eta}{\sqrt{\hat{v}_t}+\epsilon}\left( \beta _1\hat{m}_{t}+\frac{\left( 1-\beta _1 \right) g_t}{1-\beta _{1}^{t}} \right)$

5. NadaMax = AdaMax + NAG

还是这条公式

$w_{t+1}=w_t-\frac{\eta}{\sqrt{\hat{v}_t}+\epsilon}\left( \beta _1\hat{m}_{t}+\frac{\left( 1-\beta _1 \right) g_t}{1-\beta _{1}^{t}} \right)$

然后便是AdaMax的精髓部分, 注意， $\sqrt{\hat{v}_t}+\epsilon$ "相对"等价于 $u_{t}$
$u_{t}=\max \left(\beta_{2} \cdot u_{t-1},\left|g_{t}\right|\right) \\ \Delta w = \frac{\alpha}{1-\beta _{1}^{t}}\frac{m_t}{u_t}$

用 $u_{t}$ 替换 $\sqrt{\hat{v}_t}+\epsilon$
$w_{t+1}=w_t-\frac{\eta}{r_i}\left( \beta _1\hat{m}_t+\frac{\left( 1-\beta _1 \right) g_t}{1-\beta _{1}^{t}} \right) \\ r_i\,\,=\,\,\max \left( \beta _2\cdot u_{t-1},\left| g_t \right| \right)$

(得好好看看原文，这部分不是很懂)

6. AMSGrad = Adagrad Plus

尽管自适应学习率方法已成为训练神经网络的范式，但在在某些情况下，例如对于对象识别或机器翻译，它们无法收敛到最优解，甚至还被SGD+动量法超过.

Reddi .etc 此论文正式化(formalize)了这个问题，并指出 past squared gradients 的指数移动平均值，将其作为自适应学习率方法的泛化行为不佳的原因。回想一下，引入指数加权平均的动机很强：防止学习率随着训练的进行而变得无限小，即Adagrad算法的关键缺陷。但是，在其他情况下，梯度的这种短期记忆反而成为障碍。

在Adam收敛到次优解的环境中，已经观察到一些小批次的优化(minibatches)提供了较大且信息丰富的梯度，但是由于这些小批次优化很少出现，因此指数平均会减小其影响，从而导致收敛性较差。此文作者提供了一个简单的凸优化问题的例子，其中Adam可以观察到相同的行为。

AMSGrad, Reddi .etc 提出的解决方案，即采用 MAX 函数来取代指数加权平均

其动量定义,跟Adam的一样
$v_{t}=\beta_{2} v_{t-1}+\left(1-\beta_{2}\right) g_{t}^{2}$
$\hat{v}_{t}$ 的定义与Adam的不一样了
$\hat{v}_{t}=\max \left(\hat{v}_{t-1}, v_{t}\right)$
作为对比，Adam的定义
$\widehat{v}_t\gets \frac{v_t}{\left( 1-\beta _{2}^{t} \right)}$

这样，Adma 的步长便不会增加，也就规避了先前的问题

完整公式(作者还简化了)
$\begin{aligned} m_{t} &=\beta_{1} m_{t-1}+\left(1-\beta_{1}\right) g_{t} \\ v_{t} &=\beta_{2} v_{t-1}+\left(1-\beta_{2}\right) g_{t}^{2} \\ \hat{v}_{t} &=\max \left(\hat{v}_{t-1}, v_{t}\right) \\ w_{t+1} &=w_{t}-\frac{\eta}{\sqrt{\hat{v}_{t}}+\epsilon} m_{t} \end{aligned}$

AMSGrad实验–官方

以上实验用的可视化(待测试)https://github.com/bokeh/bokeh

待学习

https://ruder.io/deep-learning-optimization-2017/
近年的优化器
添加代码
论文查看

Reference

超棒的文章！
从SGD到NadaMax，十种机器学习优化算法原理及实现

各种优化器对比–BGD/SGD/MBGD/MSGD/NAG/Adagrad/Adam

深度学习——优化器算法Optimizer详解（BGD、SGD、MBGD、Momentum、NAG、Adagrad、Adadelta、RMSprop、Adam）

CSC321 Lecture 7

I. Goodfellow, Y. Bengio和A. Courville, Deep Learning. MIT Press, 2016. （花书）

概率论中「矩」（moment）的实际含义是什么，高阶矩表示数据的哪些状态？

Adam paper

L1范数与L2范数的区别

(Reddi, Sashank J., Kale, Satyen, & Kumar, Sanjiv. On the Convergence of Adam and Beyond. Proceedings of ICLR 2018.)

感恩，这篇文章极好
An overview of gradient descent optimization algorithms

eziaowonder

关注

3
点赞
踩
6

收藏

觉得还不错? 一键收藏
0
评论
深度学习优化器+公式推导

基础优化1. GD — 梯度下降1.1 BGD — 批量梯度下降代码1.2 SGD — 随机梯度下降代码1.3 MBGD — 小批量梯度下降代码2. Momentum2.1 Simple momentum update2.2 Nesterov momentum update (Nesterov Accelerated Gradient) (NAG)3. Adaptive learning rate optimization algorithm3.1.
复制链接

扫一扫